アルファベットを用いた数学の計算式が文字式(代数式)です。中学や高校の数学ではほぼ文字式を用いた計算になるため、どのように文字式を利用するのか理解しなければいけません。
いくつもの文字式が組み合わさった式を多項式といいます。多項式の計算では、掛け算・割り算をすることが頻繁にあります。そのため足し算や引き算だけでなく、どのように多項式の掛け算と割り算をするのか理解しなければいけません。
これを理解するためには、分配法則を学ぶ必要があります。分配法則を理解するからこそ、多項式の掛け算と割り算を行えるようになります。
また多項式の掛け算と割り算を学べば、代入の計算も行えるようになります。これら多項式の掛け算と割り算や代入について、やり方を解説していきます。
もくじ
式の展開:分配法則でかっこを外せる
数学にはいくつか法則があります。その中で重要な法則の一つが分配法則です。数学を学ぶのであれば、全員が分配法則を利用します。
分配法則とは、かっこを外すことのできる法則だと理解しましょう。具体的には、以下のようになります。
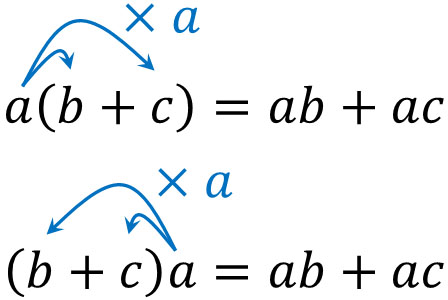
最も基本的な公式の一つであり、多項式の計算では頻繁に利用されます。分配法則を利用することで、かっこを外して足し算または引き算の式に直すことができます。
なお、かっこを外すことを数学では「展開する」といいます。数学の問題で「展開しなさい」と書かれていた場合、分配法則を利用してかっこを外すことを意味しています。
分配法則が成り立つ理由は面積で考える
それでは、なぜ分配法則が成立するのでしょうか。この理由としては、面積の足し算で考えると理解しやすいです。分配法則は小学校や中学校の数学で学びます。なぜ小学校で学ぶことがあるかというと、面積という非常に簡単な計算にて、分配法則が成り立つ理由を説明できるからです。
長方形の面積を出すとき、以下の公式を利用します。
- たて × 横 = 面積
そのため、以下にある2つの長方形の面積は以下の式によって計算できます。
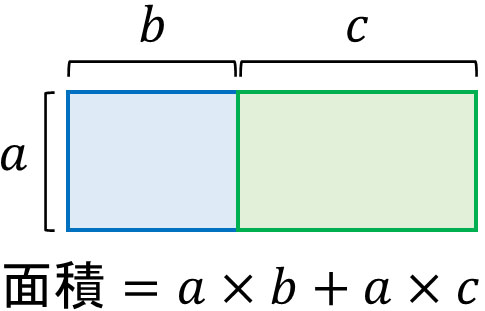
ただ、面積を計算するときは先に横の長さの足し算をしても問題ありません。つまり、先に\(b+c\)をするのです。
\((b+c)\)の足し算によって横の長さを出した後、たての長さである\(a\)を掛けます。この方法によっても、2つの長方形の合計面積を出せます。
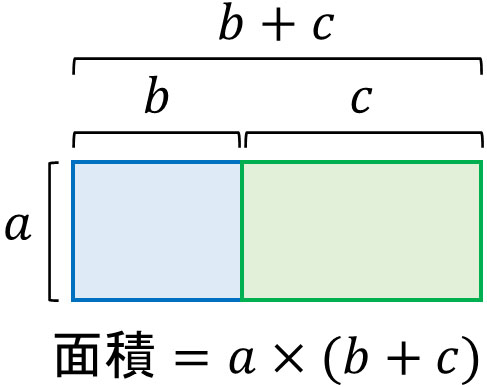
ここから、以下の公式が成立することが分かります。
- \(a(b+c)=ab+ac\)
中学以上の数学では、すべての人が式の展開で分配法則を利用します。分配法則が成り立つ理由としては、このように小学校の算数で説明できます。
文字式(代数式)の掛け算と割り算で分配法則を使う
アルファベットを用いた掛け算をする場合、分配法則を理解していなければ計算することができません。文字式では、先ほど説明した公式を頻繁に利用します。
文字式(代数式)では、以下のような式を展開しなければいけない場面がたくさんあります。このような式はどのように解けばいいのでしょうか。
- \(2(3x-4y)\)
- \(3a(a+3)\)
分配法則は数字だけでなく、文字についても成立します。そこで式の展開をするとき、以下のようにかっこ内の式すべてに掛け算をします。
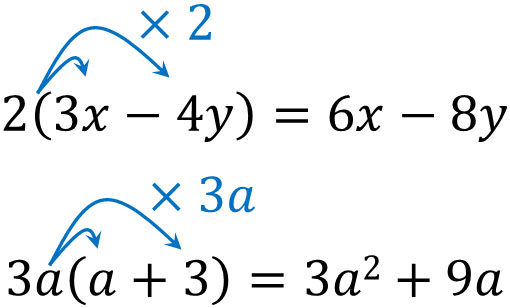
かっこの中にプラスやマイナスを含む式がある場合、それぞれすべてに対して掛けるようにしましょう。
マイナスや分数でかっこ内すべての数を掛ける
ただ分配法則を利用して計算するとき、計算ミスが発生することがよくあります。多項式の掛け算と割り算では、以下で計算ミスが起こりやすくなっています。
- マイナスの掛け算
- 分数の掛け算
分配法則では、かっこの中にあるすべての式に対して掛け算をします。そのため、分配法則によってマイナスの掛け算をする場合、かっこ内にある式すべてにマイナスをかけるようにしましょう。つまり、すべての符合が変わります。
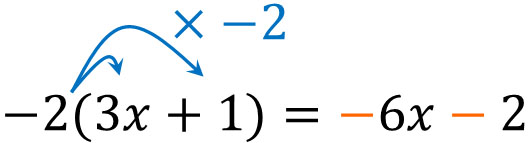
式の展開をするとき、かっこ内にある式の一方だけ符合を変えるのは間違いです。例えば、以下の計算は間違いです。
- \(-2(3x+1)=-6x\color{red}{+}2\)
同じことは分数でもいえます。分数の掛け算では、マイナスが分数の前にある場合、以下のようにしなければいけません。
- \(-\displaystyle\frac{2x-3}{4}=\displaystyle\frac{-2x+3}{4}\)
\(-\displaystyle\frac{2x-3}{4}\)というのは、\(\displaystyle\frac{-(2x-3)}{4}\)と意味が同じです。そこでかっこを外すとき、符合が正しいかどうか確認するようにしましょう。
割り算は分数の掛け算に直し、約分まで行う
なお数学の計算では、文字式を習った後はすべての式で割り算を利用しません。逆数を利用することで、必ず分数の掛け算に直します。ただ逆数を取るとき、分子と分母の向きに注意するようにしましょう。
例えば、\(\displaystyle\frac{2}{3}x=\displaystyle\frac{2x}{3}\)です。そのため、\(\displaystyle\frac{2}{3}x\)の逆数は\(\displaystyle\frac{3}{2x}\)です。\(\displaystyle\frac{2}{3}x\)を逆数にするとき、\(\displaystyle\frac{3}{2}x\)としてはいけません。
そのため、例えば以下のような計算になります。

文字式の掛け算(または割り算)では、このように計算ミスをするポイントが複数存在します。どの部分で計算ミスが発生するのか理解し、符合や逆数が正しいか確認するようにしましょう。
代入により、代数式に数字を入れる
それでは、なぜ多項式の計算を学ぶ必要があるのでしょうか。それは、簡単な計算に直すことができるからです。
なぜ数学を学ぶ必要があるのかというと、日常生活で頻繁に利用されるからです。科学だけでなく、簿記やプログラミング、マーケティングなどあらゆる場面で数学を利用した計算をします。そこで文字の式を作り、数字を入れることで答えを出します。
例えば、以下の式があるとします。
- \(3x+1\)
この式に対して、どのような数字を当てはめるのかによって以下のように答えが変わります。

このように、文字式に数字を当てはめることを代入といいます。代入することによって、あなたが求めている答えを出せるようになります。
多項式の計算で式を簡単にする
代入を利用することで、特定の答えを出せるようになります。例えば\(x=3\)であれば、代入によって以下のようになります。
- \(2x-2=2×3-2=4\)
- \(x^2=3×3=9\)
文字式が単純な場合、苦労することなく問題を解けます。一方で\(x=-3、y=2\)のとき、以下の式に代入すると答えはどのようになるでしょうか。
- \(-3(3x-5y)+4(8x-4y)\)
この式に対して代入することで計算しても問題ありません。ただ、計算は非常に複雑です。
- \(-3\{3×(-3)-5×2\}+4\{8×(-3)-4×2\}\)
そこで文字式では、先に文字式の計算をします。そのため、以下のようになります。
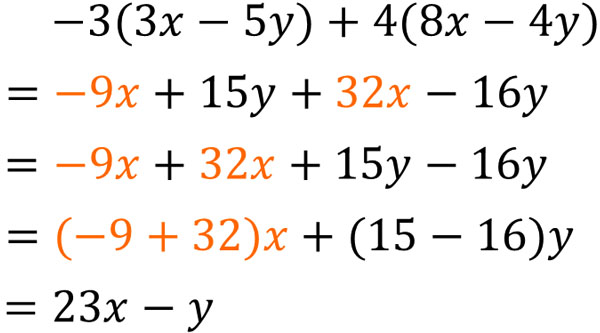
文字式(代数式)を計算することで\(23x-y\)を出します。足し算・引き算・掛け算・割り算によって文字式を簡単にした後であれば、代入するときの計算が容易です。\(x=-3、y=2\)のとき、以下のようになります。
\(23x-y\)
\(=23×(-3)-2\)
\(=-69-2=-71\)
代入をするとき、先に文字式の計算をします。その後、アルファベットに数字を代入して答えを出しましょう。
練習問題:多項式の計算と代入
Q1. 次の計算をしましょう
- \(3(4x+3)-4(2x-1)\)
- \(\displaystyle\frac{2x+3}{2}-\displaystyle\frac{x+4}{3}\)
A1. 解答
多項式の掛け算では、かっこを外すときに注意しなければいけません。かっこの前にマイナスがある場合、かっこを外すときにすべての符合が変わります。
同じことは分数にもいえます。分数の前にマイナスがある場合、分配法則によって符合が変わります。そのため、以下のような計算になります。
(a)
\(3(4x+3)-4(2x-1)\)
\(=12x+9-8x+4\)
\(=4x+13\)
(b)

Q2. \(x=3、y=-2\)のとき、次の計算をしましょう
- \(-3(2x+2y)+2(4x-5y)\)
- \((2x^2+4xy)÷\displaystyle\frac{2}{3}x\)
A2. 解答
代入の計算問題では、文字式を先に計算しましょう。そうすれば、数字を代入するときの計算が容易です。
(a)
\(-3(2x+2y)+2(4x-5y)\)
\(=-6x-6y+8x-10y\)
\(=2x-16y\)
- \(x=3、y=-2\)を代入する
\(2x-16y\)
\(=2×3-16×(-2)\)
\(=6+32=38\)
(b)
\((2x^2+4xy)÷\displaystyle\frac{2}{3}x\) : \(x\)を分子に移動
\(=(2x^2+4xy)÷\displaystyle\frac{2x}{3}\) : 掛け算に直す
\(=(2x^2+4xy)×\displaystyle\frac{3}{2x}\) : 分配法則
\(=2x^2×\displaystyle\frac{3}{2x}+4xy×\displaystyle\frac{3}{2x}\) : 約分する
\(=3x+6y\)
- \(x=3、y=-2\)を代入する
\(3x+6y\)
\(=3×3+6×(-2)\)
\(=9-12=-3\)
分配法則と多項式計算のやり方を学ぶ
数学はほぼ文字式(代数式)での計算になります。そのため、どのように多項式を計算するのか理解しなければいけません。足し算や引き算を学んだあと、次に重要なのが多項式の掛け算と割り算です。
多項式の掛け算(または割り算)をするためには、分配法則を学ばなければいけません。なぜ、分配法則が成立するのかについて、やり方を分かりやすく解説したため、分配法則の原理を理解しましょう。
また、分配法則を利用して文字式の計算をするとき、多くの人が計算ミスをするポイントがあります。以下の部分になります。
- かっこの前にマイナスが存在する
- 分数の前にマイナスが存在する
- 逆数を利用し、割り算を分数の掛け算に直す
かっこや分数の前にマイナスがある場合、分配法則によって式を展開するとき、符合がプラスなのかマイナスなのか注意しましょう。また逆数を利用するとき、文字が分子にあるのか分母にあるのか確認しましょう。これらに注意して計算すれば、ミスを防げるようになります。






