乗法公式による式の展開と因数分解：中学数学の多項式計算

中学数学ではアルファベットを用いた文字式を学びます。記号同士の足し算や引き算、掛け算、割り算をすることで計算します。

このとき数学の計算では、かっこを用いた計算をすることが頻繁にあります。掛け算の中でも、かっこ同士の掛け算では乗法公式と呼ばれる公式を利用します。

また乗法公式を学べば、因数分解を行えるようになります。多項式を「かっこを利用した掛け算の式」に直すのが因数分解です。多項式の計算では、乗法公式を使う式の展開に比べて、因数分解のほうが難しいため、どう計算するのか理解しなければいけません。

乗法公式と因数分解を一緒に学ぶと、数学を理解しやすくなります。どのように乗法公式を利用し、因数分解の問題を解けばいいのか解説していきます。

分配法則で多項式同士の掛け算を証明する

多項式の計算では、式の展開をさせる問題が非常にたくさん出されます。かっこを外し、単項式の足し算と引き算の式にすることを「展開する」といいます。このとき、かっこ同士の計算ではより式の展開が複雑になります。

具体的には、以下の計算をすることがあります。

• \((a+b)(c+d)\)

つまり、\((a+b)\)と\((c+d)\)の掛け算をします。このような多項式の計算では、どのようにすればいいのでしょうか。

多項式同士の掛け算では、以下のように式の展開をします。

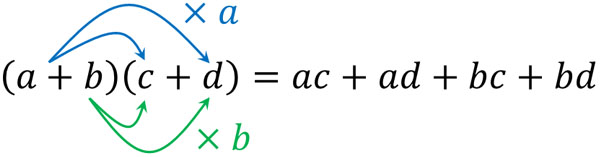
なぜ、このように式の展開をすることができるのでしょうか。数学では、理由を理解しなければいけません。そこで、この公式が成立する証明をしてみましょう。

文字式（代数式）を習っていることから分かる通り、数字は文字に置きかえることができます。そこで、\((c+d)\)を\(N\)に置きかえてみましょう。そうすると、\((a+b)(c+d)\)は\((a+b)N\)となります。そのため、分配法則を利用することで以下のように計算できます。

• \((a+b)N=aN+bN\)

\(N\)は\((c+d)\)です。そこで、\(N=(c+d)\)を代入します。その結果、以下のような計算になります。

\(aN+bN\)

\(=a(c+d)+b(c+d)\)

\(=ac+ad+bc+bd\)

ここから、\((a+b)(c+d)=ac+ad+bc+bd\)が成り立つと証明できます。多項式同士の計算では、この式を利用して式の展開が可能です。

ただ、数学の計算をするときに上記の公式の証明を毎回することはありません。そこで、この公式が成立することを理解して、計算方法を覚えましょう。どのように式の展開をすればいいのか、やり方を覚えるのです。

4つの乗法公式を使った式の展開

なお、先ほど説明した公式を利用することで、乗法公式が成立することを理解できます。乗法公式とは、式の展開や因数分解をするときに利用する公式を指します。

乗法公式は主に4つあります。それぞれ、以下のようになります。

• \((x+a)(x+b)=x^2+(a+b)x+ab\)
• \((x+a)^2=x^2+2ax+a^2\)
• \((x-a)^2=x^2-2ax+a^2\)
• \((x+a)(x-a)=x^2-a^2\)

この4つの乗法公式はすべて覚えるようにしましょう。そうしなければ、効率的に多項式の計算をすることができません。

なぜ、この公式が成立するのか証明するのは簡単です。前に説明した公式を利用することで、乗法公式になります。それぞれを確認していきます。

・乗法公式：その1

\((x+a)(x+b)\)は以下のように計算できます。

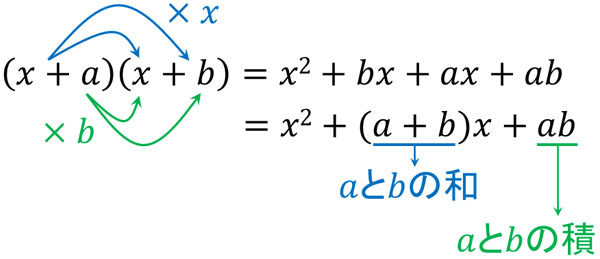
式を展開することで、\((x+a)(x+b)=x^2+(a+b)x+ab\)となることが分かります。数学で最も頻繁に利用する乗法公式であり、必ず覚えるようにしましょう。

例えば、\((x+1)(x+3)\)の問題を解く場合、乗法公式を利用すると以下のように式を展開できます。

\((x+1)(x+3)\)

\(=x^2+(1+3)x+1×3\)

\(=x^2+4x+3\)

・乗法公式：その2

同じように、多項式の展開をすることで乗法公式を出すことができます。\((x+a)^2\)は以下のようになります。

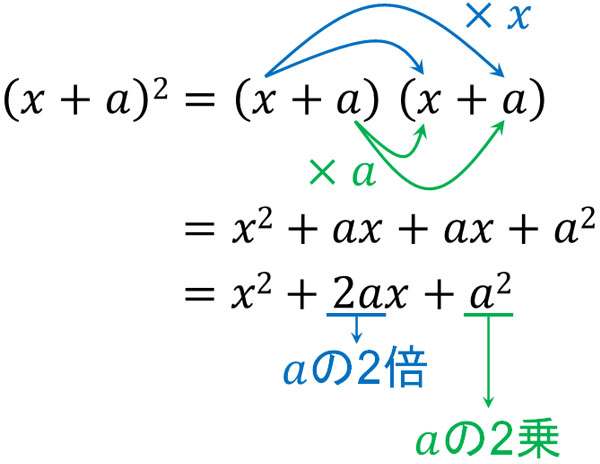
前の乗法公式では、\(a\)と\(b\)の数字が違っていました。一方でこの乗法公式では、\((x+a)\)の二乗を計算しています。そのため、答えは\((a+b)x\)ではなく\(2ax\)となります。また\(ab\)ではなく、\(a^2\)となります。

・乗法公式：その3

それに対して、\((x-a)^2\)は以下のようになります。

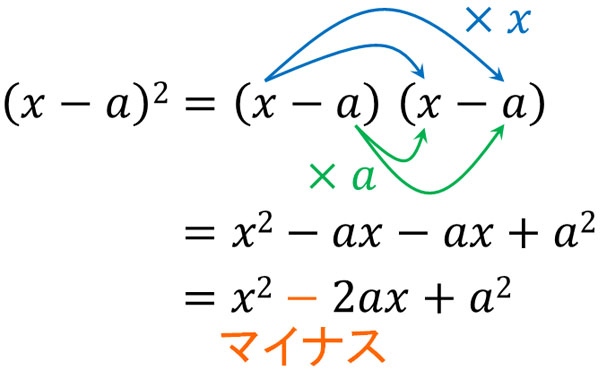
\((x+a)^2\)に対して、\((x-a)^2\)では符合がマイナスになっています。そのため、\(2ax\)ではなく\(-2ax\)となります。プラスがマイナスになっただけですが、乗法公式では重要です。なお、\(a^2\)となるのは\((x+a)^2\)と同じです。

・乗法公式：その4

\((x+a)(x-a)\)の乗法公式は以下のように計算できます。

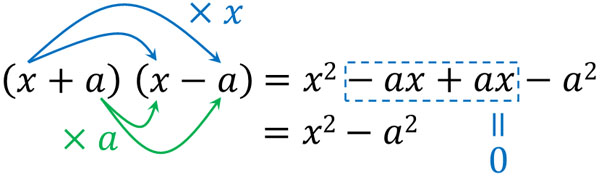
\(-ax+ax=0\)です。そのため、\((x+a)(x-a)\)を計算すると\(x^2-a^2\)となります。

他の乗法公式に比べると、\((x+a)(x-a)=x^2-a^2\)を利用するケースは少ないです。ただ、乗法公式として必ず覚えなければいけません。

乗法公式を忘れても計算は可能

なお場合によっては、4つの乗法公式を忘れてしまうこともあります。その場合であっても問題はありません。\((a+b)(c+d)=ac+ad+bc+bd\)の計算をすればいいからです。

例えば、\((x-3)^2\)の計算をするとします。先に述べた乗法公式を利用すれば、\(x^2-6x+9\)の答えをすぐに出すことができます。ただ乗法公式を忘れたとしても、それぞれの掛け算をすることで式を展開することができます。以下のようになります。

\((x-3)^2\)

\(=(x-3)(x-3)\)

\(=x^2-3x-3x+9\)

\(=x^2-6x+9\)

乗法公式を覚えていれば、こうした計算を省いて答えを出すことができます。ただ忘れてしまったとしても、計算することで答えを出すことができます。

因数分解：かっこの式を作る

数学で式の展開について学んだあと、次に勉強するのが因数分解です。かっこを外すのが式の展開です。一方で因数分解とは何なのでしょうか。因数分解とは、式の展開の逆だと理解しましょう。つまり、かっこのない式からかっこのある式を作ります。

積を作っている一つの式を因数といいます。足し算と引き算によって成り立っている式について、因数同士の掛け算となるように分解するのです。

因数分解では、共通する因数（共通因数）を見つけます。例えば、以下のようになります。

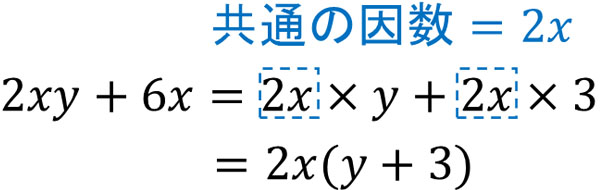
式の展開に比べると、因数分解のほうが難しいです。式の展開では、どの数字の掛け算をすればいいのか明確に分かっています。一方で因数分解では、共通因数を探す必要があります。共通因数が書かれているわけではないため、何が共通因数になるのか考えなければいけません。

因数分解は複数の選択肢がある

また因数分解の場合、多くは乗法公式を利用した問題が出されます。つまり乗法公式を覚えていなければ、因数分解することができません。式の展開では、乗法公式を忘れてしまったとしても答えを出すことができます。一方、因数分解では乗法公式を覚えておくのが必須です。

なお乗法公式を利用する因数分解では、複数の選択肢が存在します。その中から、最適な答えを出さなければいけません。

例えば、以下の式の因数分解はどのようにすればいいのでしょうか。

• \(x^2+4x+3\)

先ほど説明した通り、乗法公式は4つあります。つまり、4つの選択肢の中から最適な乗法公式を選ばなければいけません。なお乗法公式の中では、因数分解で最も頻繁に利用されるのが以下の公式です。

• \((x+a)(x+b)=x^2+(a+b)x+ab\)

\(x^2+4x+3\)と\(x^2+(a+b)x+ab\)を比べると、以下のようにならなければいけません。

• \(a+b=4\)
• \(ab=3\)

この2つの条件を満たす因数を見つけなければいけません。このとき因数分解のやり方が存在します。それは、掛け算に着目することがあります。

・足し算と引き算は無限に答えが存在する

\(a+b=4\)となるように\(a\)と\(b\)を当てはめる場合、無限に答えが存在します。例えば、以下のようになります。

• \(2+2=4\)
• \(10-6=4\)
• \(-100+104=4\)

そのため、因数分解をするとき\(a+b\)に最初に着目することはありません。そうではなく、掛け算である\(ab\)に着目します。\(ab=3\)となる整数は以下の2つだけです。

• \(1×3=3\)
• \(-1×(-3)=3\)

つまり、因数分解するとき答えの候補が2つあります。このうち、どちらが正解なのでしょうか。そこで次に、\(a+b=4\)に当てはまる数字を探します。以下のようになります。

• \(a=1,b=3\)ならば、\(1+3=4\)
• \(a=-1,b=-3\)ならば、\(-1+(-3)=-4\)

\(a=1,b=3\)であれば、\(a+b=4\)かつ\(ab=3\)の両方を満たします。そのため、以下のように因数分解できます。

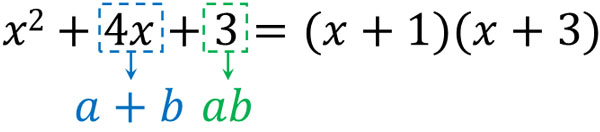
このように、因数分解では複数の候補から正しい答えを導き出さなければいけません。今回は簡単な式の因数分解を例として使いました。ただ、式が複雑になる場合はより因数分解が難しくなります。

4パターンの公式を使って因数分解する

前述の通り、乗法公式には4つの公式があります。そのため、中学数学の因数分解では、4つある乗法公式の中でどれを利用するのか選択しなければいけません。因数分解は他に公式があるものの、それらは高校などより難易度の高い数学を学ぶときに覚えましょう。

因数分解で利用する乗法公式の見分け方としては、累乗が含まれているかどうか確認しましょう。4つある乗法公式のうち、以下の3つの公式には累乗が含まれています。

• \((x+a)^2=x^2+2ax+\color{red}{a^2}\)
• \((x-a)^2=x^2-2ax+\color{red}{a^2}\)
• \((x+a)(x-a)=x^2-\color{red}{a^2}\)

累乗が含まれている場合、これらの乗法公式を利用して因数分解できる可能性があります。例えば、以下の多項式はどのように因数分解できるのでしょうか。

• \(x^2+6x+9\)
• \(x^2-6x+9\)

\(3^2=9\)です。そのため、これらの多項式には累乗が含まれていると分かります。また、3を2倍すると6になります。そのため、以下のように因数分解できます。

累乗することができ、さらに数を2倍することで\(2ax\)（または\(-2ax\))となる場合、乗法公式を利用した因数分解が可能です。

一方で以下の場合はどのように因数分解できるでしょうか。

• \(x^2-25\)

\(5^2=25\)であり、この式には累乗が含まれています。またマイナスの符合があり、\(2ax\)または\((a+b)x\)の部分が存在しません。この条件に当てはまる場合、以下の因数分解が可能です。

このようにして、乗法公式を利用して因数分解をします。

・累乗できない場合の因数分解

それに対して、式の中に累乗を含まないなど、先ほど説明した3つの乗法公式を利用できないケースがよくあります。その場合、以下の乗法公式を利用して因数分解をします。

• \((x+a)(x+b)=x^2+(a+b)x+ab\)

この乗法公式を利用して因数分解する方法は既に説明しました。因数分解ではこの乗法公式を最も頻繁に利用します。いずれにしても、因数分解では複数の選択肢の中から答えを出せるようにしましょう。

練習問題：乗法公式と因数分解の計算

Q1. 次の式を展開しましょう

1. \((x-3)(x+5)\)
2. \((x+4)^2-(2x+3)(x-6)\)

A1. 解答

乗法公式を利用することで、式の展開をすることができます。

(a)

\((x-3)(x+5)=x^2+2x-15\)

(b)

\((x+4)^2-(2x+3)(x-6)\)

\(=x^2+8x+16-(2x^2-12x+3x-18)\)

\(=x^2+8x+16-2x^2+12x-3x+18\)

\(=-x^2+17x+34\)

Q2. 次の式の因数分解をしましょう

1. \(x^2-6x-16\)
2. \(x^2y-49y\)
3. \((2x+3)(2x-3)-5x(x-2)\)

A2. 解答

乗法公式を利用すれば因数分解できます。また、式の展開をしたあとに因数分解することもあります。

(a)

因数分解では、最初に掛け算に着目します。そこで、\(x^2-6x\color{red}{-16}\)の-16を確認しましょう。掛け算で-16になる数字としては、以下の候補があります。

• \(1×(-16)=-16\)
• \(-1×16=-16\)
• \(2×(-8)=-16\)
• \(-2×8=-16\)
• \(4×(-4)=-16\)

これらの候補の中で、\(a+b=-6\)になる数字はどれでしょうか。\(a=2,b=-8\)のとき、\(a+b=-6\)になります。そのため、以下のように因数分解できます。

• \(x^2-6x-16=(x+2)(x-8)\)

(b)

因数分解では、必ずしも最初に乗法公式を利用するとは限りません。共通因数をまとめたあと、乗法公式を利用するケースもあります。

\(x^2\color{red}{y}-49\color{red}{y}\)では、\(y\)が共通因数です。そのため最初の因数分解は以下のようになります。

• \(x^2y-49y=y(x^2-49)\)

重要なのは、\((x^2-49)\)がさらに因数分解できることです。そのため、以下のように因数分解できます。

• \(y(x^2-49)=y(x+7)(x-7)\)

(c)

式の展開をした後、因数分解することがあります。そこで、先に以下の計算をします。

\(\color{red}{(2x+3)(2x-3)}-5x(x-2)\)

\(=\color{red}{4x^2-9}-5x^2+10x\)

\(=-x^2+10x-9\)

このように式の展開をした後、因数分解をします。この式の因数分解は以下のようになります。

\(-x^2+10x-9\)

\(=-(x^2-10x+9)\)

\(=-(x-1)(x-9)\)

Q3. 次の式の因数分解をしましょう

• \((x+2)(x-2)+y(2x+y)\)

A3. 解答

最初に式の展開をしなければいけません。そのため、以下のようになります。

\((x+2)(x-2)+y(2x+y)\)

\(=x^2-4+2xy+y^2\)

\(=x^2+2xy+y^2-4\)

この後、どのように因数分解をすればいいのでしょうか。この式では、以下のように2つに分けて考えます。

• \(\color{red}{x^2+2xy+y^2}-4\)

このとき\(x^2+2xy+y^2\)に着目すると、以下のように因数分解できます。

\(\color{red}{x^2+2xy+y^2}-4\)

\(=(x+y)^2-4\)

しかし、まだ掛け算だけの式になっていません。つまり、さらに因数分解しなければいけません。そこで式を確認すると、\(4=2^2\)と気づくことができます。

また\((x+y)\)では分かりにくいため、\((x+y)=N\)に置きかえてみましょう。そうすると、以下のようになります。

• \(\color{red}{(x+y)}^2-4=\color{red}{N}^2-2^2\)

このように式を置き換えることで、乗法公式を使用して因数分解できることに気が付きます。以下のように因数分解できます。

• \(N^2–2^2=(N+2)(N-2)\)

ただ、\(N=x+y\)です。そこで\(N=x+y\)を代入することで、以下のように因数分解が完了します。

• \((N+2)(N-2)=(x+y+2)(x+y-2)\)

乗法公式と因数分解を利用し、多項式の問題を解く

数学で乗法公式と因数分解は、セットで理解するべき内容です。そこで乗法公式を利用した式の展開は当然として、因数分解を行えるようにしましょう。

乗法公式は必ず覚えなければいけません。そこで4つの乗法公式を利用できるようにしましょう。式の展開では、乗法公式を覚えなくても答えを出すことができます。一方で因数分解では、乗法公式を覚えていなければ答えを出せません。

乗法公式を利用した式の展開に比べて、因数分解は数字の候補が多く、答えを出すのが難しくなります。ただ乗法公式を利用するという意味では、式の展開も因数分解も同じです。

中学数学で重要な内容の一つが、乗法公式を使う式の展開と因数分解です。乗法公式を利用し、どのように式の展開や因数分解をすればいいのか理解するようにしましょう。