数学を学ぶとき、負の数を理解しなければいけません。正の整数だけを学んでいたときとは異なり、0の概念や足し算・引き算を学ぶことで複雑な計算ができるようになります。
0よりも小さい数が存在するというと、奇妙に思うかもしれません。ただ、私たちは日常生活の多くの場面で負の数を利用しています。そのため、正の整数だけでなく負の整数を利用して計算することは非常に重要です。
それでは、0やマイナスの概念とは何なのでしょうか。どのようにして、正の数と負の数を考えて計算すればいいのでしょうか。
中学一年生で数学を学ぶとき、全員が正の数と負の数を理解しなければいけません。ここでは正と負の整数の計算方法について、問題を交えながら解説していきます。
もくじ
0(ゼロ)は基準を示すときに用いられる
一般的には、0(ゼロ)は何もないことを示します。例えば100円を持っていたとしても、使ってしまえば持っているお金は0円です。
存在しないことがゼロなのであれば、マイナスという概念は意味が分かりません。負の整数を学ぶとき、多くの人が混乱するのは、「存在しないものよりも下に数字が存在する」と考えてしまうことがあります。
ただ、0は存在しないことを示すだけではありません。他にも意味があります。それは基準です。ゼロを一つの基準にすることで、0よりも数字が大きいのか、それとも小さいのかによって正の数と負の数を使います。
例えば私たちの日常生活では温度を利用します。温度には0℃という基準があります。0℃よりも気温が低ければ、数字はマイナスになります。雪が降る街であれば、多くの人がマイナスの気温を経験することになります。

このように考えると、プラスの数だけでなく、マイナスの数を利用するのは変なことではないと分かります。0には基準を示す意味も含まれているため、多くの人が日常生活で負の数を利用しています。
正の整数(自然数)、負の整数は基準からの増減を表す
0に基準という概念があることを学べば、プラスやマイナスの整数が何を意味しているのか理解できるようになります。正の整数(自然数)や負の整数というのは、基準となる点(ゼロ)からどれだけズレているのかを表します。
以下の図では、0を基準にして、右にある数字は正の整数(自然数)です。
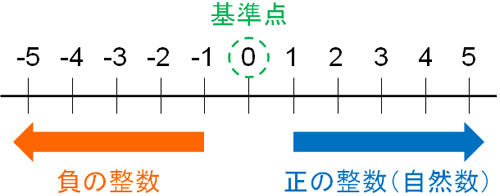
一方で、0よりも左にある数字は負の整数です。プラスとマイナスを利用することで、基準からの増減を表すことができます。
例えば、ダイエットすることで体重を減らすことを考えます。その場合、いま現在の体重を基準(ゼロ)にする人が大多数です。いまよりも体重が3kg減ったのであれば、-3kgのダイエットに成功したといえます。
・プラスとマイナスは言いかえることができる
そのため、プラスとマイナスの数は言いかえることができます。例えば、以下は同じ意味です。
- 体重が3kg減った
- 体重が-3kg増えた
また、以下も意味は同じです。
- 温度が5℃下がる
- 温度が-5℃上がる
これらの言いかえが可能であることを理解することが、正の数と負の数を学ぶときに重要です。
大小の見分け方と絶対値
それでは、正の数と負の数で数字の大小はどのように見分ければいいのでしょか。これを理解するためには、絶対値の概念について理解する必要があります。
ゼロを基準にして、プラスとマイナスの数を確認すればいいことは理解しました。数字の大小を見分けるとき、ゼロからどれだけ離れているのか確認しましょう。プラスやマイナスに関わらず、0からどれだけ数字がずれているのかを示すのが絶対値です。
例えば、4の絶対値は4です。一方で-3の絶対値は3です。0から左に3つ進めば、-3になります。0からの距離は3のため、-3の絶対値は3になるのです。
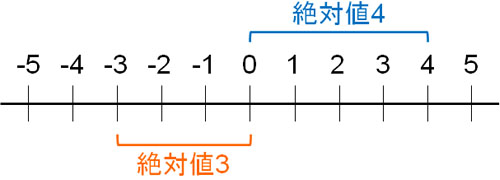
この考え方を学べば、数の大小を見分けられるようになります。例えば5と3では、5のほうが数字は大きいと分かります。そのため、5>3と表せます。それに対して-3と-5では、どちらのほうが数字は大きいのでしょうか。
-3の絶対値は3です。また、-5の絶対値は5です。重要なのは、負の数は数字(絶対値)が大きいほど数が小さくなる事実です。-3よりも、-5のほうが絶対値は大きいです。そのため-3のほうが大きい数字であり、\(-3>-5\)と表すことができます。
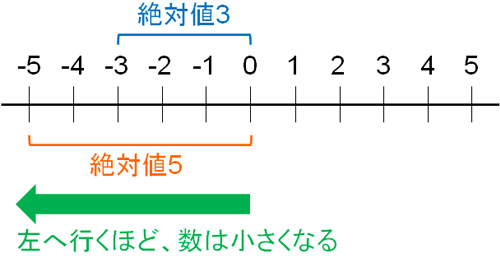
数が大きいにも関わらず、マイナスが付くことで小さい数字になるのは奇妙に思うかもしれません。ただ、これについても私たちは日常生活の中で利用しています。
例えば-3℃と-20℃では、-20℃のほうが寒いです。これは、-20℃のほうが大きい負の数だからです。数字(絶対値)は大きかったとしても、負の数では小さい数になることを理解しましょう。
正の数の足し算・引き算:加法と減法
0やマイナスの概念を理解することで、正の数と負の数について、足し算(加法)と引き算(減法)を理解できるようになります。
正の数と負の数については、正の数の足し算と引き算から学ぶと理解しやすいです。プラスの数を取り扱うとき、以下の2種類があります。
- 正の数の足し算
- 正の数の引き算
それぞれ、どのようになっているのでしょうか。
正の数の足し算でかっこを用いる
正の数の足し算(加法)については、小学校などの算数で既に習っています。そのため、正の数と正の数の足し算については、特に苦労することなく理解できるはずです。例えば、以下の計算は容易です。
- \(3+1=4\)
このとき、\(3+1\)は以下のように表すこともできます。
- \(3+(+1)\)
- \((+3)+(+1)\)
どれも意味は同じです。足し算では、+を2つ並べることができます。ただ、++と表記するのではなく、かっこを用いて表記します。
・負の数に対して正の数を加える
それでは、マイナスの数字に対してプラスの数字を加える場合はどのようにすればいいのでしょうか。例えば、以下の計算がこれに該当します。
- \(-5+3\)
「\(-5+(+3)\)」「\((-5)+(+3)\)」と表すこともできます。いずれにしても、この計算では-5に3を加えます。つまり、-5よりも3大きい数字を解答しなければいけません。
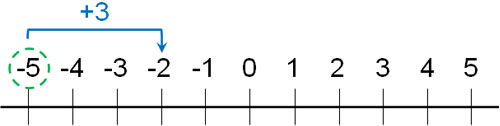
-5の絶対値は5です。-5に+3をすることで、右に3つ進むと、-2になります。そのため、答えは-2です。
正の数の引き算をするルール
それに対して、正の数の引き算はどのように考えればいいのでしょうか。例えば、以下の計算があるとします。
- \(3-2=1\)
この計算についても、小学校で既に学んでいます。重要なのは、以下の計算式に置きかえられることです。
- \(3-(+2)=1\)
- \((+3)-(+2)=1\)
すべての数字は+が隠れています。例えば私たちが2や3の数字を使うとき、+2や+3と表すことができます。正の整数(自然数)について、+は省略することができます。ただ詳細に記載すると、「\(3-2\)」は「\(3-(+2)\)」と表せるのです。
・負の数に正の数の引き算をする
もちろん、マイナスの数字に対して正の数(自然数)の引き算をすることはよくあります。例えば、以下の計算の答えは何でしょうか。
- \(-1-3\)
この式は「\(-1-(+3)\)」「\((-1)-(+3)\)」と置きかえることもできます。-1から+3を引くため、-1よりも3小さい数を解答しなければいけません。
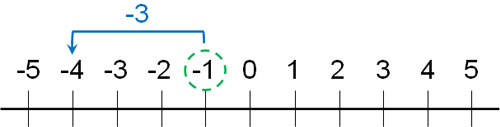
そのため、答えは-4になります。
- \(-1-3=-4\)
- \(-1-(+3)=-4\)
- \((-1)-(+3)=-4\)
このように計算します。
負の数の足し算・引き算
プラスの数字について解説してきましたが、正の数の足し算と引き算について理解するのは難しくありません。問題なのは、負の数に対する足し算と引き算です。
- マイナスを加える
- マイナスを差し引く
これらはどういう意味なのでしょうか。例えば、「\(1-(-3)\)」を計算するとき、以下のようになります。
- \(1-(-3)=1+3=4\)
多くの人は理由を理解せずに、計算方法を覚えようとします。ただ、本来は理由を理解しなければいけまさえん。そこで、なぜこのようになるのかを含めて解説していきます。
言いかえにより、負の数の足し算を学ぶ
マイナスの数を加える計算は頻繁に出されます。例えば、以下の計算はどのように考えればいいのでしょうか。
- \(2+(-4)\)
前述の通り、数字は言いかえをすることができます。例えば体重が2kg減れば、「体重が-2kg増えた」と言いかえることができます。「体重が増える」という表現ではあっても、-2kgのプラスであるため、体重は減っています。
このように、プラスとマイナスは置きかえることができます。つまり、以下のように言いかえできます。
- \(2-4\):4減った
- \(2+(-4)\):-4増えた
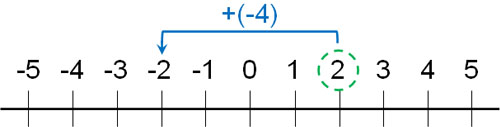
2から4を引くと、-2になります。2から4小さい数は-2です。負の数の加えるとは、要は正の数の引き算と同じだと理解しましょう。
マイナスの引き算がプラスになる理由
負の数を理解するとき、多くの人で混乱するのはマイナスの引き算です。これまで説明してきたのは以下の内容です。
- プラスの数(正の整数)の足し算
- プラスの数(正の整数)の引き算
- マイナスの数(負の整数)の足し算
正の数の足し算や引き算は既に小学校で学んでいます。またマイナスの数の足し算については、言いかえすることで、正の数(自然数)の引き算だと考えることができます。一方で、例えば以下の計算はどのようにすればいいのでしょうか。
- \(2-(-3)\)
この計算についても、言いかえすることができます。マイナスの記号は、反対の意味があります。前述の通り2kg減ったという表現は、-2kg増えたと言いかえることが可能です。
それでは、-3kg減ったという表現を言いかえれば、どのようになるのでしょうか。マイナスは反対の性質になるため、-3kg減ったというのは、3kg増えたことを意味します。マイナスのマイナスはプラスなのです。
これが、マイナスの数の引き算をするとき、プラスに置きかえできる理由です。
- \(2-(-3)=2+3=5\)
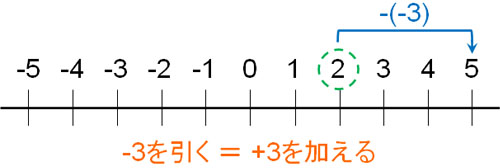
重要なのは、「マイナスは反対の意味を有する」ことです。なぜ、マイナスを引くとプラスになるのか、中学数学で理解できない人はたくさんいます。そこでマイナスに反対の意味があり、言いかえできることを理解すれば、この理由が分かるようになります。
練習問題:正の数と負の数の足し算・引き算
Q1. 次の数の大小について、不等号を使って表しましょう
- \(-2、4、-3\)
- \(-0.3、-3、0\)
A1. 解答
マイナスの数については、数字(絶対値)が大きいほど数が小さいです。正の数とは逆の考えになるため、不等号の順番は以下のようになります。
- \(4>-2>-3\)
- \(0>-0.3>-3\)
例えば(b)であれば、0と0.3と3を比べたとき、数字の大きい順に「\(3>0.3>0\)」になります。マイナスでは反対に数字(絶対値)が大きいほど数は小さくなるため、「\(0>-0.3>-3\)」となります。
Q2. 次の計算をしましょう
- \(7-(+3)\)
- \(-0.5+(-0.2)\)
- \(-3-(-6)\)
- \(\displaystyle\frac{1}{2}-\left(-\displaystyle\frac{1}{3}\right)\)
- \(-3+(-2)-(-6)-5\)
A2. 解答
正の数と負の数の計算では、かっこを用いた計算を言いかえるようにしましょう。中学数学でも高校数学でも、全員が符合の置きかえをした後に計算します。置きかえのポイントは以下のようになります。
- \(+\)と\(+\):\(+\)
- \(+\)と\(-\):\(-\)
- \(-\)と\(+\):\(-\)
- \(-\)と\(-\):\(+\)
小数でも分数でも、足し算と引き算ではすべてこのように言いかえできます。そのため、以下のように計算できます。
(a)
\(7-(+3)=7-3=4\)
(b)
\(-0.5+(-0.2)=-0.5-0.2=-0.7\)
(c)
\(-3-(-6)=-3+6=3\)
(d)
\(\displaystyle\frac{1}{2}-\left(-\displaystyle\frac{1}{3}\right)\)
\(=\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}\)
\(=\displaystyle\frac{3}{6}+\displaystyle\frac{2}{6}=\displaystyle\frac{5}{6}\)
(e)
\(-3+(-2)-(-6)-5\)
\(=-3-2+6-5=-4\)
プラスとマイナスについて、言いかえしなければ問題を解くことはできません。足し算になるのか、それとも引き算になるのか、必ず確認しましょう。符合の置きかえさえ行えば、あとは小学校の算数の内容になるため、足し算または引き算をするだけです。
分数については、符合の言いかえをした後、分母を合わせる必要があるので少し複雑です。ただ、分数の計算は小学校で習っているはずなので難しくないはずです。
Q3. 次の計算をしましょう
下の表は、A~Dの4人が160cmから何cm高いかを示しています。
| A | B | C | D | |
| 160cmからの違い (cm) | 12 | -4 | 7 | -9 |
- 最も身長の高い人は、最も身長が低い人よりも何cm高いでしょうか
- 4人の身長の平均を求めましょう
A3. 解答
a. 最も身長の高い人は、最も身長が低い人よりも何cm高いでしょうか
最も身長の高い人はAです。また、最も身長の低い人はDです。Aは身長が+12cm高く、Dは9cm低いです。
数の違いを計算するとき、引き算をしなければいけません。例えば上図によると、Aの身長は+12cmであり、Cの身長は+7cmです。AとCの身長の違いは「12cm-(+7cm)=12cm-7cm=5cm」です。これと同じように、数の比較では引き算をします。
AとDの身長差は以下の計算をします。
- \(12-(-9)=12+9=21\)
そのため最も身長の高い人は、身長が最も低い人と比べて21cm高いです。
b. 4人の身長の平均を求めましょう
身長の平均値を計算するとき、一つの方法としてAからDのそれぞれの身長を計算する方法があります。上の表を参考に計算すると、それぞれの身長は以下のようになります。
| A | B | C | D | |
| 身長の高さ (cm) | 172cm | 156cm | 167cm | 151cm |
A~Dの身長を足した後、4人で割れば身長の平均値を出せます。ただ、もっと簡単な方法で平均値を求めることはできないのでしょうか。
この点について、平均していくらずれているのか計算するようにしましょう。以下のように、4人の身長は違いがあります。
- \(A:+12\)cm
- \(B:-4\)cm
- \(C:7\)cm
- \(D:-9\)cm
4人の身長差の平均はいくらでしょうか。4人の身長差を合計すると、以下のようになります。
\(12+(-4)+7+(-9)\)
\(=12-4+7-9=6\)
4人の身長差の合計は6cmです。合計値を人数分で割れば、平均値を算出できます。つまり、一人あたり160cmから何cm高いのか(または低いのか)について、平均値を出すことができます。
6cm(合計値)を4人で割ると、「\(6÷4=1.5\)」です。つまり4人の身長は平均して、160cmよりも+1.5cm高いことが分かります。そのため、4人の身長の平均値は161.5cmです。
\(160+1.5=161.5\)
プラスとマイナスの数字を使い、足し算と引き算をする
負の数を習うとき、多くの人が混乱します。0(ゼロ)よりも低い値がなぜ存在するのか、理解できません。またマイナスの引き算がなぜプラスになるのか、大人でさえ理由を説明できない人が大多数です。
ただここで説明した通り、日常生活であってもマイナスの数字を利用する場面は非常に多いことに気が付きます。0には基準値という意味があり、絶対値によって数の大小を比較します。
また、実際にプラスとマイナスの数字を使って足し算(加法)と引き算(減法)をする場合、かっこを利用する場面がほとんどです。かっこを用いる計算では、必ず置きかえが可能です。高校や大学で難解な問題を解くときであっても、すべての人が置きかえをしているため、必ず置きかえをした後に計算するようにしましょう。
これらのルールを学べば、正の整数(自然数)と負の整数を用いた足し算・引き算の問題を解けるようになります。小数や分数でもやり方は同じです。特にマイナスの引き算で問題を解くのに苦労する人が多いため、なぜそうなるのか理由を含めて理解するようにしましょう。