私たちにとって身近であり、日常生活でひんぱんに利用する単位がV(ボルト)です。電位の単位がボルトです。
高い場所にある物体は位置エネルギーをもちます。電気についても、高い場所にある電荷であるほど位置エネルギーも高いです。電位というのは、位置エネルギーの計算に必要な高さ(電気的な高さ)を表しているのです。
なお位置エネルギーは仕事と意味が同じです。そのためボルトと移動距離を利用して仕事量(内部エネルギー)の計算が可能です。また電場と距離を利用すれば、電位を得ることができます。他には、電位と電場では力学的エネルギー保存則も成り立ちます。
力学で学んだことを電磁気学でも利用しましょう。そこで、電位と電場の関係や公式の作り方、位置エネルギーの計算方法を解説していきます。
もくじ
電位の定義と公式、位置エネルギーの関係
まず、電位とは何かを学びましょう。電気的な高さを電位と呼びます。また、単位はV(ボルト)です。力学では、高さ\(h\)にある物体は位置エネルギーをもちます。電気についても、高さとして電位\(V\)が存在します。
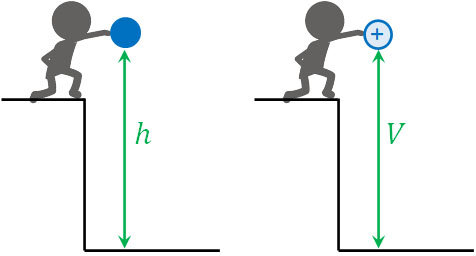
電位\(V\)が電気の高さに該当すると理解すれば、電位に関する公式を覚えやすくなります。それでは、電位の定義は何なのでしょうか。以下が電位の定義になります。
- +1Cの点電荷がもつ位置エネルギー
電位を理解するため、力学での位置エネルギーと比較しましょう。力学で学ぶ位置エネルギーは\(mgh\)で表すことができます。\(m\)が重さ(質量)、\(g\)が重力加速度、\(h\)が高さです。
電気では、質量\(m\)に該当するのが電気量\(q\)です。また、重力加速度\(g\)と高さ\(h\)の積に該当するのが\(V\)です。そのため、電気での位置エネルギー\(U\)は以下のように表すことができます。
- \(U=qV\)
電位の定義より、\(q=1\)の場合、\(U=V\)です。いずれにしても、力学で内部エネルギーを電気バージョンに変換することで、電位を用いた内部エネルギーの公式を得ることができます。
外力による仕事と静電気力の内部エネルギー
なお力学では、仕事と内部エネルギーは同じ意味をもつと習います。質量\(m\)の物体に加わる力(重力)は\(mg\)です。この物体を高さ\(h\)へもっていくために必要な仕事\(W\)は\(W=mgh\)です。外から力を加えることによって仕事\(W\)をすると、その分だけ内部エネルギー\(U\)が上昇します。
電気でも同じであり、外力による仕事\(W\)と静電気力の内部エネルギー\(U\)は式が同じです。
・外力による仕事\(W\)
電気量\(q\)の点電荷を電位\(V\)まで移動させるために必要な外力による仕事\(W\)は以下の式によって表すことができます。
- \(W=qV\)
・静電気力の内部エネルギー\(U\)
電気量\(q\)の点電荷が電位\(V\)の場所にあるとき、点電荷が保有している静電気力の内部エネルギーは以下の式によって表すことができます。
- \(U=qV\)
力学では、物体を持ち上げることで仕事をすると、その分だけ内部エネルギーが上昇します。電気についても同じ現象が起こると考えましょう。
一様な電場での電位と移動距離の関係
次に、電位と電場の関係を確認しましょう。先ほど、「力学では内部エネルギーを\(mgh\)と表すものの、電気では\(qV\)と表す」と解説しました。前述の通り、力学での\(gh\)は電位\(V\)に相当します。これが何を意味しているのか理解しましょう。
以下のように一様な電場\(E\)が存在し、電気量\(q\)の点電荷の移動距離を\(d\)としましょう。力学での内部エネルギーと比較すると、以下のようになります。
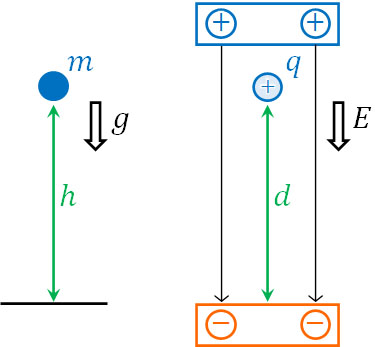
物体の重さ\(m\)に対応するのが電気量\(q\)です。また地球には場が存在し、重力加速度\(g\)が場に該当します。電気で場に該当するのは電場\(E\)です。つまり、重力加速度\(g\)は電場\(E\)に相当します。
また力学での高さ\(h\)について、電気では点電荷の移動距離\(d\)に相当します。そのため、以下の関係が成り立ちます。
- 物体の重さ\(m\) ⇔ 電気量\(q\)
- 重力加速度\(g\) ⇔ 電場\(E\)
- 高さ\(h\) ⇔ 移動距離\(d\)
そこで力学での内部エネルギー\(U=mgh\)を静電気力の内部エネルギー\(U=qEd\)に変えましょう。つまり、力学の内部エネルギーと静電気力の内部エネルギーは式が同じです。
電位\(V\)と電場\(E\)、距離\(d\)には\(V=Ed\)の関係がある
これまでの説明より、内部エネルギー\(U\)を\(U=qEd\)と記すことができますし、\(U=qV\)と記すこともできます。そのため式を見てわかる通り、以下の関係が成り立ちます。
- \(V=Ed\)
1kgの物体がもつ位置エネルギーは\(gh\)です。同様に、1Cの点電荷がもつ位置エネルギー(=電位\(V\))は\(Ed\)です。そのため、\(V=Ed\)となるのです。そこで\(V=Ed\)を変形し、以下の式にしましょう。
- \(E=\displaystyle\frac{V}{d}\)
イメージとしては、点電荷\(q\)が横幅\(d\)、高さ\(V\)の坂を転がっている場面を想像しましょう。
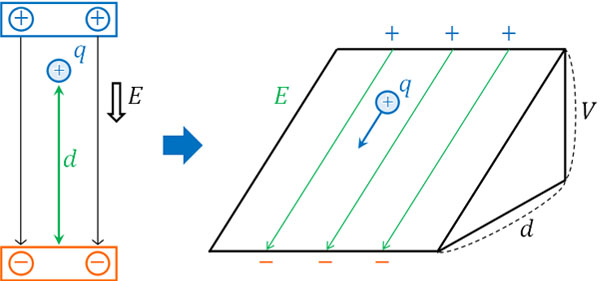
一様な電場では、電場\(E\)は一定です。そのため、上図のような坂を作ることができます。また高さ\(V\)が大きいほど、横幅\(d\)が小さいほど、斜面の傾き\(E\)は急になります。
また\(E\)の値は一定であるため、\(V=Ed\)は下図のように一次方程式になります。
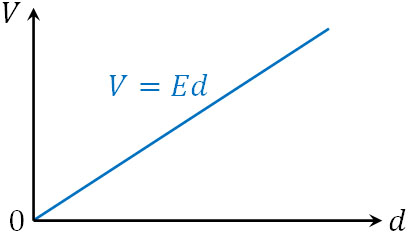
つまり電場\(E\)は電位\(V\)による傾きを表しています。\(E=\displaystyle\frac{V}{d}\)というのは、傾きを計算しているのと意味が同じなのです。
電場\(E\)の単位はN/Cです。これに加えて、電場\(E\)はV/mによって表すことができます。電場にはN/CとV/mの2つの単位があるのです。両方とも電場を表すことができ、どちらの単位を利用しても問題ありません。
点電荷による電位と公式、電位の足し算
それでは一様な電場ではなく、点電荷による電位はどのように計算すればいいのでしょうか。点電荷による電位\(V\)の公式を得るとき、積分が必要になります。そのため点電荷による電位を得る公式の導出は行わず、結果を記すと以下のようになります。
- \(V=k\displaystyle\frac{Q}{r}\)
点電荷による電場は\(E=k\displaystyle\frac{Q}{r^2}\)で表すことができます。この式を積分すると\(V=k\displaystyle\frac{Q}{r}\)になり、電場と電位の公式は似ています。
なお点電荷によって電場が作られる場合の内部エネルギーを計算したい場合、\(V=k\displaystyle\frac{Q}{r}\)を\(U=qV\)へ代入しましょう。そうすると、以下の式を得られます。
- \(U=k\displaystyle\frac{qQ}{r}\)
こうして、点電荷によって電場が作られるときの内部エネルギーを得ることができます。
・複数の点電位が存在する場合の電位\(V\)
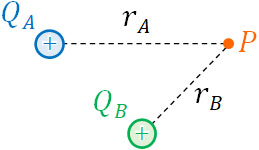
このとき、複数の点電位が存在する場合の電位\(V\)はいくらになるでしょうか。方法は簡単であり、それぞれの電位を足しましょう。例えば2つの点電荷\(Q_A\)と\(Q_B\)がある場合、点Pの電位\(V_P\)は以下のように表すことができます。
\(V_P=V_A+V_B\)
\(V_P=k\displaystyle\frac{Q_A}{r_A}+k\displaystyle\frac{Q_B}{r_B}\)
足し算によって電位を得ることができるため、公式を利用すれば計算は難しくありません。
点電荷による電位の公式の導出
参考までに、点電荷による電位の公式の導出を記します。積分をすることになるため公式を暗記し、この部分を読み飛ばしても問題ありません。なお、積分の初歩を学んでいる場合は計算できます。
位置エネルギーは自由に基準点を設定できます。そこで無限遠(∞)を基準にしましょう。無限に遠い場所では、位置エネルギーは0です。
また\(U=qV\)であり、電荷が1Cの場合は\(U=V\)です。前述の通り、「+1Cの点電荷がもつ位置エネルギー」が電荷の定義です。
なお電荷が1Cの場合、力\(F\)と電場\(E\)が等しくなることは既に学んでいると思います。\(F=qE\)であるため、電荷が1Cでは\(F=E\)となるのです。つまり電荷が1Cの場合、点電荷の力は以下のようになります。
- \(F=k\displaystyle\frac{Q}{r^2}\)
仕事\(W\)を計算するためには、力\(F\)と移動距離\(d\)のグラフについて面積を計算すればいいです。つまり、無限遠から距離\(r\)へ移動させるために必要な仕事量(面積)を計算するのです。ただ静電気力\(F=k\displaystyle\frac{Q}{r^2}\)は曲線であるため、積分をしましょう。
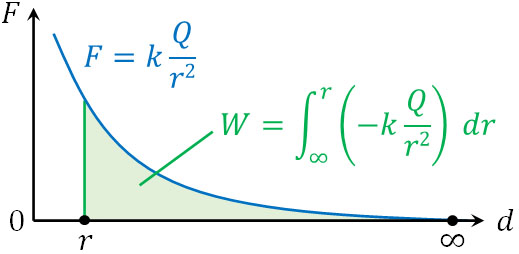
無限遠から距離\(r\)へ移動させるため、必要な力は\(F=-k\displaystyle\frac{Q}{r^2}\)です。このとき、以下の式によって面積を計算できます。
\(W=\displaystyle \int_{∞}^{r} \left(-k\displaystyle\frac{Q}{r^2}\right) dr\)
\(=-kQ\displaystyle \int_{∞}^{r} \left(\displaystyle\frac{1}{r^2}\right) dr\)
\(=-kQ\displaystyle \int_{∞}^{r} r^{-2} dr\)
\(=-kQ\left[-\displaystyle\frac{1}{r}\right]_{∞}^{r}\)
\(=-kQ\left(-\displaystyle\frac{1}{r}-0\right)\)
\(=\displaystyle\frac{kQ}{r}\)
なお仕事\(W\)と内部エネルギー\(U\)は同じなので、\(W=U\)です。また\(U=qV\)より、\(q=1\)の場合は\(U=V\)です。そのため仕事\(W\)を電位\(V\)に変えることにより、以下の公式が成り立ちます。
- \(V=\displaystyle\frac{kQ}{r}\)
積分の初歩を利用することにより、点電荷による電位の公式を導出することができました。高校数学で積分を学んでいる人であれば、全員が点電荷による電位の公式を得ることができます。ただ積分によって公式を得るのは大変なので、点電荷による電位を得るときは公式を覚えると計算が速くなります。
静電気による位置エネルギーの力学的エネルギー保存則
なお力学では、力学的エネルギー保存則を学びます。電気についても、力学的エネルギー保存則を利用することができます。つまり、運動エネルギーと内部エネルギーの合計は常に同じになるのです。
- 運動エネルギー + 位置エネルギー = 一定
力学で学んだことは電磁気でも利用できます。例えば点Aに質量\(m\)、電気量\(q\)の粒子を一様な電場\(E\)に置き、電場の影響を受けて粒子が移動する場合、距離\(d\)の場所にある粒子が負の金属板に到達するときの速さを以下のように計算できます。
\(qEd=\displaystyle\frac{1}{2}mv^2\)
\(v^2=\displaystyle\frac{2qEd}{m}\)
\(v=\sqrt{\displaystyle\frac{2qEd}{m}}\)
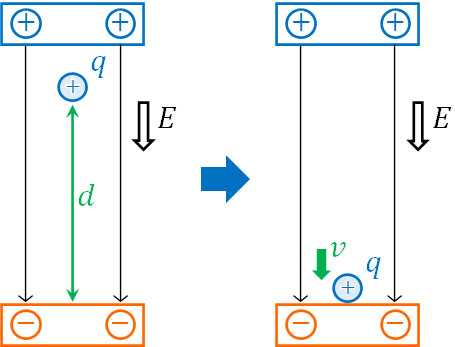
これまで説明した通り、\(U=qV=qEd\)です。内部エネルギーがすべて運動エネルギーに変換されるため、先ほど記した式を作ることができます。
電場による仕事に関する練習問題
それでは、電位と電場が関わる練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 2つの金属板A(正電荷)と金属板B(負電荷)が距離\(d\)で平行に存在しています。下図のように金属板に電池がつながっており、一様な電場\(E\)を生じています。
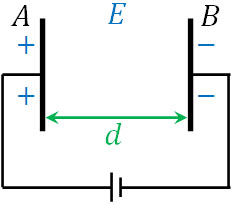
- +3Cの電荷をBからAへ移動させるために必要な仕事を求めましょう。
- 質量\(m\)、電気量\(q\)の正電荷を金属板Aから速さ\(v_0\)で発射させるとき、金属板Bに到着するときの速さはいくらですか。
1) +3Cの電荷をBからAへ移動させるために必要な仕事を求めましょう
正電荷から負電荷に向かって電場が発生するため、電場は右向きとなります。正電荷をBからAに移動させるためには、電場の向きに逆らって正の力を加える必要があるため、仕事の符号はプラスでなければいけません。
また一様な電場では、静電気力は\(F=qE\)によって計算できます。そこで力\(F\)と移動距離\(d\)をかけることによって仕事\(W\)を計算しましょう。
\(W=Fd\)
\(W=3Ed\)
こうして、必要な仕事量は\(W=3Ed\)とわかります。
2) 質量\(m\)、電気量\(q\)の正電荷を金属板Aから速さ\(v_0\)で発射させるとき、金属板Bに到着するときの速さはいくらですか
力学的エネルギー保存則を利用して式を作りましょう。内部エネルギーは\(U=qEd\)であるため、金属板Bに到着するときの速さを\(v\)とすると以下のようになります。
\(\displaystyle\frac{1}{2}mv_0^2+qEd=\displaystyle\frac{1}{2}mv^2\)
\(v^2=v_0^2+\displaystyle\frac{2qEd}{m}\)
\(v=\sqrt{v_0^2+\displaystyle\frac{2qEd}{m}}\)
こうして、速さは\(\sqrt{v_0^2+\displaystyle\frac{2qEd}{m}}\)と計算できました。
電位と電場の関係を学び、公式の意味を知る
物理を学ぶとき、公式を暗記しても問題を解くことはできないため、必ず公式がもつ意味を理解しましょう。電位\(V\)は1Cの点電荷がもつ位置エネルギーを表します。このとき内部エネルギーは\(U=qV\)であり、電位は\(V=Ed\)となります。
電位と電場の関係を理解するとき、力学の知識が役に立ちます。力学で内部エネルギーや仕事の計算をする方法や概念は電気の計算でも利用できます。そこで質量\(m\)を電気量\(q\)に、重力加速度\(g\)を電場\(E\)に、高さ\(h\)を距離\(d\)に変換しましょう。
また\(V=Ed\)より、\(E=\displaystyle\frac{V}{d}\)です。一様な電場では、\(E\)は電位\(V\)に対する傾きを表します。一方で点電荷による電位を計算するとき、\(V=k\displaystyle\frac{Q}{r}\)を利用しましょう。
なお静電気による位置エネルギーについても力学的エネルギー保存則を利用できます。そのため速さを計算したい場合、力学的エネルギー保存則を使いましょう。これらが電位と電場で重要な公式の意味です。






