物理で波動を学ぶとき、うなりを習います。振動数の異なる音波が重なることにより、音の強弱を生じる現象がうなりです。
物理では、うなりを生じる原理を学びます。うなりでは公式を利用することにより、振動数を計算します。ただ公式を覚えるのではなく、なぜ公式が成り立つのか理解しましょう。物理では、自然現象が発生する仕組みを学ぶのが重要になります。
それでは、うなりとは何なのでしょうか。また、どのような原理でうなりを生じるのでしょうか。ここでは、うなりの内容を解説していきます。
うなりとは何か:異なる波長による重なり
うなりを生じている場合、耳鳴りのような感覚となります。そのため、多くの人にとってうなりは不快な音です。
同じ振幅、波長、振動数、速さの波が重なると定常波を生じます。それでは同じ形の波ではなく、異なる形の波が重なる場合はどのようになるでしょうか。この場合、うなりを生じます。振動数が少し異なる音源を利用することにより、音が小さくなったり大きくなったりします。
例えば以下のように、振動数が少し異なる波を同時に発生させるとうなりを生じます。
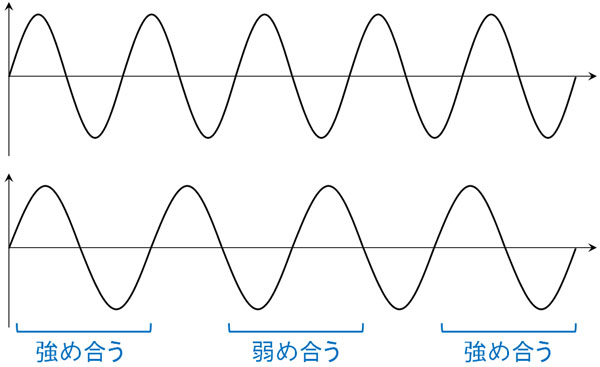
図を確認すると、2つの波が存在することにより、同位相によって強め合う部分があれば、逆位相によって弱め合う部分もあります。
異なる波長を重ねると、音の強弱が表れる
それでは、先ほどの波を重ね合わせてみましょう。波は足し算によって計算でき、重ねることによって合計での波の高さは変化します。以下のようになります。
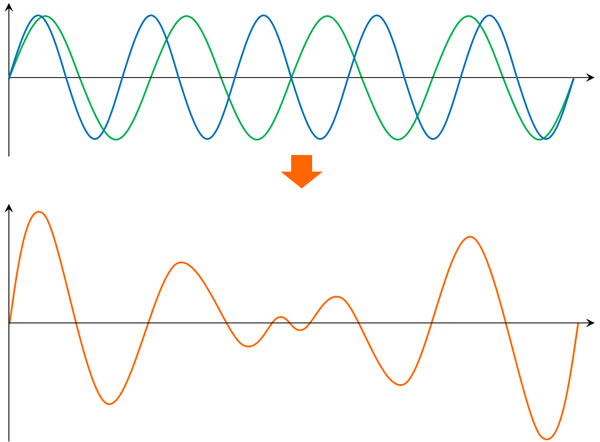
振動数の異なる波を重ね合わせることによって、図のように振幅が大きくなったり小さくなったりしていることがわかります。うなりで音の大小を生じるのはこうした理由があります。
うなりを習うとき、多くの人は公式を覚えます。ただ公式を見ても、うなりの原理を理解できません。そこで図を利用し、なぜうなりを生じるのか学びましょう。
うなりの公式と導出
それでは、うなりの公式を確認しましょう。1秒間に何回、うなりを生じるのかを表すのがうなりの振動数\(f\)です。うなりを発生させている2つの音源について、それぞれの振動数が\(f_1\)と\(f_1\)の場合、以下の公式が成り立ちます。
- \(f=|f_1-f_2|\)
うなりの公式は簡単であるため、内容を理解せずに公式を覚えて計算問題を解くことは可能です。ただ、それでは物理を学ぶ意味がないため、なぜこの公式によってうなりの振動数を計算できるのか学びましょう。
まず、うなりの周期を\(T\)とします。例えば下図の場合、波1と波2を比べると、波の数の差は1つです。
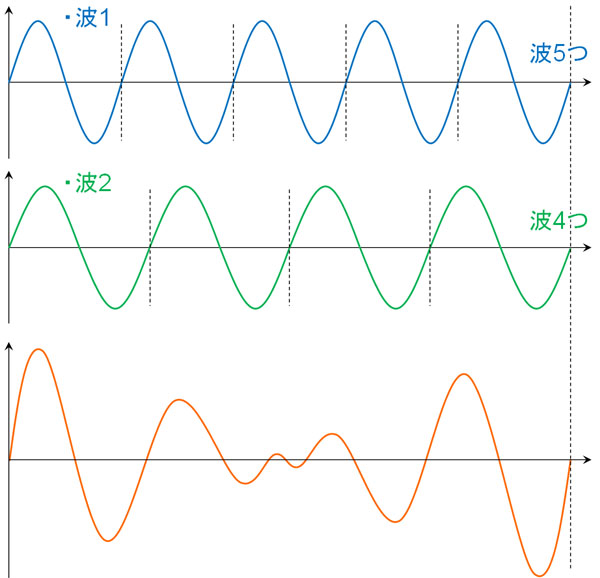
うなりで大きな音が聞こえるのは、波1と波2が同位相のときです。また、時間経過と共に位相がずれることで、図のように音が小さくなります。その後、位相が重なることで音は再び大きくなります。
波の形が異なる場合であっても、時間経過によって必ずいつかは同位相となります。このとき2つの波が再び同位相となり、重なるためには、1波長分のズレを考慮すればいいです。
イメージとしては、運動場でトラックを走る場面を考えましょう。波1と波2が同時にスタートしても、波1のほうが速い場合、波1と波2の位置は異なります。ただ、どこかの時点で波1は波2に追いつくことで重なります。
周回遅れになるというのは、一周分のトラック距離の差があることを意味します。
波であれば、再び同位相になって強め合うためには、波1が波2よりも速く振動し、波2の位相に追いつけばいいとわかります。言い換えると、波1が素早く振動した結果、波1の振動数は波2よりも一回多くなり、同位相となれば再び強め合います。
振動数の差が1であればいいため、以下のようになります。
- \(|\)波1の振動数\(-\)波2の振動数\(|=1\)
波1と波2について、どちらの振動数が多くても問題ないように、絶対値を加えましょう。
また波1の振動数\(f_1\)というのは、1秒間に波1が\(f_1\)回振動することを意味します。言い換えると、1秒間に波1が\(f_1\)個存在します。そのため\(T\)秒(うなりの周期)に存在する波1の数は\(f_1T\)です。
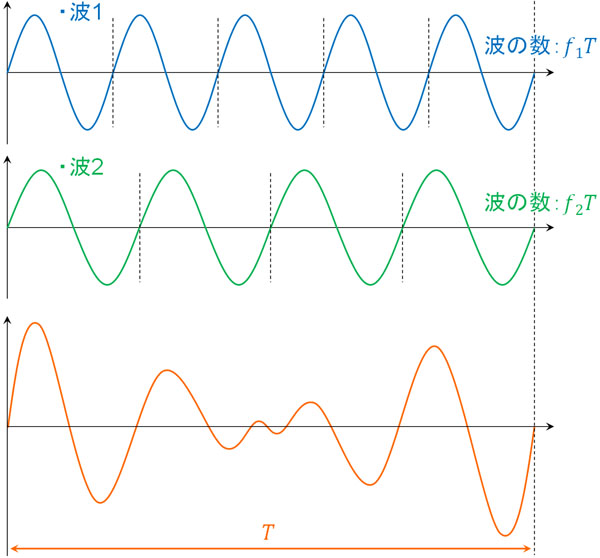
同様に考えると、\(T\)秒の間に存在する波2の数は\(f_2T\)です。つまり、以下の式が成り立ちます。
- \(|f_1T-f_2T|=1\)
この式を変形しましょう。
\(|f_1T-f_2T|=1\)
\(|f_1-f_2|=\displaystyle\frac{1}{T}\)
\(|f_1-f_2|=f\)
こうして、うなりの公式を得ることができました。公式を暗記するのではなく、なぜ公式が成り立つのか学びましょう。そうしなければ、物理を勉強する意味がありません。
うなりに関する練習問題
それでは、うなりに関する物理の問題を解いてみましょう。以下の答えは何でしょうか。
- 振動数が不明な音さAと振動数410zの音さBを同時に鳴らすと、3秒間に6回のうなりが聞こえました。次に、音さAと振動数415Hzの音さCを同時に鳴らすと、4秒間に12回のうなりが聞こえました。音さAの振動数はいくらでしょうか。
うなりで振動数を得るため、\(|f_1-f_2|=f\)を利用しましょう。また、音さAの振動数を\(f\)とします。3秒間に6回のうなりが聞こえる場合、うなりの振動数は2Hzです。1秒間に何回の振動をするのかを表すのが振動数だからです。そのため、以下の式を作りましょう。
\(|f-410|=2\)
そのため、\(f\)は412または408です。
なお4秒間に12回のうなりが聞こえる場合、うなりの振動数は3Hzです。振動数415Hzの音さCを使用しているため、以下の式を作れます。
\(|f-415|=3\)
そのため、fは418または412です。
前述の通り3秒間に6回のうなりが聞こえる場合、\(f\)は412または408であり、両方の式を満たすのは412です。そのため、音さAの振動数は412Hzであるとわかります。
うなりを生じる原理と公式を得る方法を理解する
異なる2つの波が重なる場合、定常波ではなくうなりを生じます。波の位相が異なることにより、音が強め合ったり弱め合ったりします。その結果、時間経過によって強い音が聞こえたり、音が弱くなったりします。
物理でうなりを学ぶとき、公式を覚えることになります。ただ、多くの教科書は公式を記載しているものの、なぜ公式を得られるのか説明していません。
しかし、物理は世の中の自然現象を学ぶ学問であり、公式を暗記する学問ではありません。公式を覚えて問題を解けるようになっても意味がないのです。
うなりの公式は単純です。ただ公式を覚えるだけでなく、うなりを生じる理由や公式を導出する過程を含めて理解しましょう。これにより、うなりの原理がわかります。