物体には摩擦力が働きます。重い物を動かすとき、大きな力が必要になるのは摩擦力が働くからです。物理では摩擦力を学び、摩擦力には垂直抗力が関与しています。
なお、摩擦力の計算では静止している状態と動いている状態で分けて考えなければいけません。静止しているときの摩擦力が静止摩擦力であり、物体が動いているときの摩擦力が動摩擦力です。静止摩擦力と動摩擦力は性質が異なるのです。
摩擦力は垂直抗力と係数を利用して計算します。また物理では摩擦力を含めた複合問題が出されるため、どのように摩擦力を利用して計算すればいいのか学ぶ必要があります。
それでは、摩擦力の性質には何があるのでしょうか。摩擦力の種類や計算方法に加え、練習問題を含めて解説していきます。
もくじ
垂直抗力に対して摩擦力が働く
静止している物体に対して、弱い力で押しても物体は動きません。これは、摩擦力が働いているからです。物体を動かすとき、摩擦力が存在することは理解できると思います。
物体が静止している場合、必ず力がつりあっています。物体を押しても動かないのは、あなたが押している向きに対して、反対方向に同じ力(摩擦力)が働いているからです。
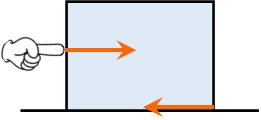
こうして力がつりあい、物体は静止します。
このとき、摩擦力の大きさに関与する力が垂直抗力です。床が物体を上に押し上げる力が垂直抗力です。同じ箱であっても、軽い箱だと摩擦力が小さいものの、箱の中に多くの物を入れることで箱全体が重くなれば摩擦力が大きくなります。この理由は箱が重くなり、その結果として垂
直抗力が大きくなるからです。
物体の重さを\(m\)とすると、重力加速度は\(g\)なので、物体の重力は\(mg\)です。そのため作用・反作用の法則により、垂直抗力\(N\)は\(mg\)です。
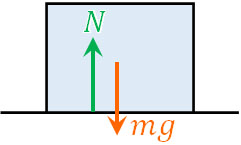
摩擦力というのは、垂直抗力\(N=mg\)に依存することを理解しましょう。
なお物体の上に別の物体を乗せると、当然ながらその分だけ垂直抗力\(N\)は上がります。乗せた物体の重さを\(m’\)とすると、この場合の垂直抗力は以下のようになります。
- \(N=mg+m’g\)
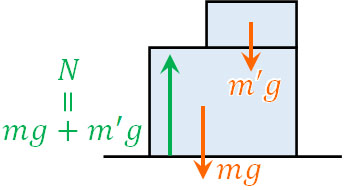
垂直抗力というのは、物体の重さによって変化します。
静止摩擦力・最大摩擦力と静止摩擦係数\(μ\)
なお垂直抗力がわかれば、静止時の最大摩擦力を計算できるわけではありません。摩擦力の計算では、垂直抗力に加えて静止摩擦係数\(μ\)を利用します。同じ物体を床に置く場合、平らな床とデコボコした床では、当然ながらデコボコしている床のほうが静止時の最大摩擦力は大きくなります。
つまり同じ物体であっても、どのような場所に置くのかによって最大摩擦力が変化します。そのため、垂直抗力に加えて静止摩擦係数\(μ\)を利用するのです。静止している物体で利用できる値が静止摩擦係数\(μ\)です。
なお、静止摩擦力はあなたがどれくらいの力で物体を押すのかによって変化します。静止している物体では、必ず力がつりあっています。そのため弱い力で押せば、弱い静止摩擦力が発生します。一方で強い力で押せば強い静止摩擦力が発生します。
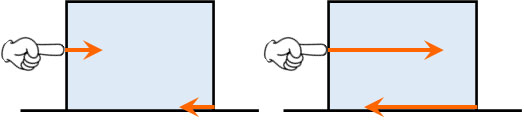
ただより強い力で押すと、どこかの時点で物体は動きます。静止摩擦力は徐々に大きくなるものの、静止摩擦力の限界よりも大きな力で押すことで、物体は静止状態から解放されます。
物体が動き出す瞬間では、静止摩擦力は最大となります。このときの静止摩擦力を最大摩擦力(最大静止摩擦力)といいます。最大摩擦力\(f\)は先ほど解説した静止摩擦係数\(μ\)を利用し、以下の式によって表されます。
- \(f=μN\)
物体を置く床の状態や環境によって静止摩擦係数\(μ\)は変化します。ただいずれにしても、静止摩擦係数\(μ\)を利用することで最大摩擦力\(f\)の計算が可能です。
物体が動いているときは動摩擦力\(f’\)が働く:動摩擦係数\(μ’\)
それでは静止している状態ではなく、物体が動いているときの摩擦力はどのように考えればいいのでしょうか。物体を動かしているときであっても、摩擦力は存在します。
物体が動いているときの摩擦力を動摩擦力といいます。なぜ最大摩擦力(最大静止摩擦力)と動摩擦力を分ける必要があるかというと、最大静止摩擦力に比べて、動摩擦力のほうが摩擦力は小さいからです。
つまり摩擦力というのは、動き出す直前が最も大きいです。一方で実際に動き始めると、動摩擦力は最大摩擦力に対して小さくなることが経験的にわかっています。動摩擦力は一定であり、動摩擦係数\(μ’\)を利用することで動摩擦力を得ることができます。
- \(f’=μ’N\)
物体が動いている場合、加える力を大きくすると加速度は大きくなります。これは、動摩擦力が一定だからです。
前述の通り、静止摩擦力はあなたが加える力によって変化します。ただ、あなたが加える力はある時点で最大摩擦力と同じになります。その後、物体が動き始めると摩擦力は最大摩擦力から動摩擦力へ変化します。そのため、あなたが加える力(外力)と摩擦力の関係は以下のようになります。
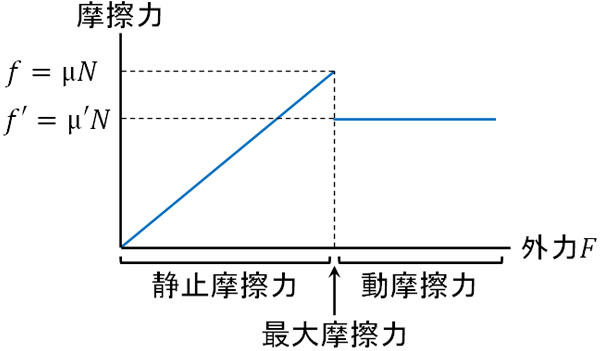
垂直抗力は同じであるものの、最大静止摩擦力よりも動摩擦力のほうが小さいです。言い換えると、静止摩擦係数よりも動摩擦係数のほうが小さいです。
なお、なぜ「最大摩擦力=動摩擦力」にならず、動摩擦力のほうが小さくなるのかについて、明確な理由を述べている教科書はありません。物理現象では、なぜその現象が起こるのか理由が不明であるケースは多いです。そこで、実験でわかっている事実をひとまず納得しましょう。
荒い斜面を動くときの物体の運動
それでは、摩擦力が発生する場面の計算問題を解いてみましょう。摩擦力で重要なのはベクトルの向きです。物体をどちらの方向へ動かすのかによって、摩擦力の向きが変化するのです。実際に物体を動かすとき、どちらの向きに摩擦力が発生するのか想像しましょう。
それでは、以下の問題の答えは何でしょうか。
- 地面との角度がθの斜面に質量\(m\)の物体を置きます。なお静止摩擦係数を\(μ\)、重力加速度を\(g\)とします。
- 物体が静止しているとき、静止摩擦力\(f\)はいくらですか。
- 物体の左側(斜面の下側)に糸をつけ、引っ張ると物体は動き始めました。加えた力\(F\)はいくらですか。
- 物体の右側(斜面の上側)に糸をつけ、引っ張ると物体は動き始めました。加えた力\(F\)はいくらですか。
1) 物体が静止しているとき、静止摩擦力\(f\)はいくらですか
力のつり合いを確認することによって静止摩擦力\(f\)を得ることができます。そこで、以下のように図を作りましょう。
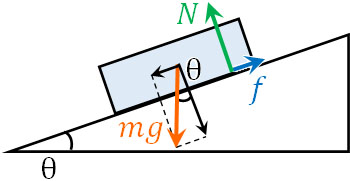
物体には重力が加わっており、斜面の下に滑りたいと考えています。ただ、それとは反対向きに静止摩擦力\(f\)が加わっています。こうした力のつり合いにより、物体は静止しています。そのため、以下の式を作ることができます。
\(f=mgsinθ\)
こうして、静止摩擦力\(f\)は\(mgsinθ\)とわかりました。
2) 物体の左側(斜面の下側)に糸をつけ、引っ張ると物体は動き始めました。加えた力\(F\)はいくらですか
力のつり合いにより、以下の式を作ることができます。
\(F+mgsinθ=f\)
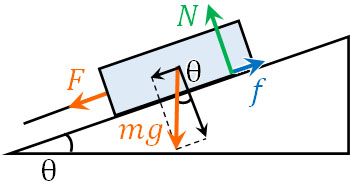
また物体が動く瞬間では、最大摩擦力が働いていることになります。垂直抗力\(N\)は\(mgcosθ\)であるため、最大摩擦力\(f\)は\(μmgcosθ\)です。
\(f=μmgcosθ\)
そこで、\(f=μmgcosθ\)を\(F+mgsinθ=f\)に代入しましょう。
\(F+mgsinθ=f\)
\(F=μmgcosθ-mgsinθ\)
\(F=mg(μcosθ-sinθ)\)
つまり\(F=mg(μcosθ-sinθ)\)の力を加えることによって、物体は斜面を下方向にすべり始めます。
3) 物体の右側(斜面の上側)に糸をつけ、引っ張ると物体は動き始めました。加えた力\(F\)はいくらですか
先ほどとは異なり、糸を物体の右側につけて引っ張ります。物体を右に引っ張るため、作用・反作用の法則により、摩擦力のベクトルは左向きになります。つまり、先ほどとは摩擦力が働く向きが逆になります。
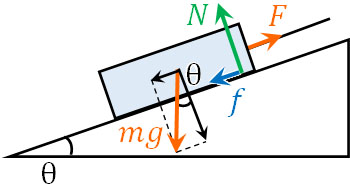
静止している状態では、物体に力を加えると反対方向に摩擦力が発生するのはこれまで説明した通り容易に理解できると思います。いずれにしても、摩擦力がどちらの向きに発生するのか理解しましょう。
この場合、力のつり合いは以下のようになります。
\(F=f+mgsinθ\)
なお最大摩擦力\(f\)は\(μmgcosθ\)なので、\(f=μmgcosθ\)を代入しましょう。
\(F=f+mgsinθ\)
\(F=μmgcosθ+mgsinθ\)
\(F=mg(μcosθ+sinθ)\)
こうして、\(F=mg(μcosθ+sinθ)\)の力で引っ張ることによって物体が動き始めるとわかります。
2物体の摩擦力を計算する
なお摩擦力を利用する物理の計算問題では、摩擦力のみを利用する単純な問題が出されるケースは稀です。多くの場合、複合問題を解かなければいけません。また、問題は難しいです。
ここまで、力を加える向きとは逆方向に摩擦力が働くケースを考えてきました。ただ場合によっては、力を加える向きと摩擦力が反対方向ではないケースもあります。この例として、2物体の摩擦力の計算があります。
力学でひんぱんに出題される問題が2物体の摩擦力です。上の物体、または下の物体を動かすとき、移動距離やスピードを計算するのです。例えば、以下の問題の答えは何でしょうか。
- なめらかな床の上に質量\(M\)の板Aを置きます。その上に質量\(m\)の板Bをおき、板Bに初速度\(v_0\)を加えて動かすと、板Bは板Aの上を滑った後に静止しました。なお板Aと板Bに働く動摩擦係数を\(μ’\)、重力加速度を\(g\)とします。
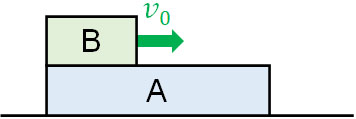
- 板Bが静止するまでの時間\(t\)はいくらですか。
- 板Bが静止した後、両物体の速さ\(v\)はいくらですか。
1) 板Bが静止するまでの時間\(t\)はいくらですか
この問題を解くため、板Aと板Bに働く力をそれぞれ記入しましょう。
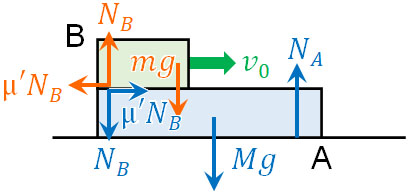
板Bに加わる力はこれまで説明した通りです。加えた力とは反対方向に摩擦力が働きます。そのため板Bは徐々にスピードが落ち、最終的に板Aの上で静止します。
一方、板Aに対しては、板Bで発生する摩擦力とは反対方向に同じ力が発生します。この力によって、板Aは加速するのです。なお、なめらかな床の上に板Aを置いているため、板Aの下面で働く摩擦力はありません。
なお、板Bとの摩擦力によって板Aは左向きの力のみを受けます。これにより、徐々にスピードが減少します。言い換えると、マイナスの加速度となっています。また、力の大きさは重さと加速度をかけることで得られます。そこで板Bの加速度を\(a_B\)とすると、以下の運動方程式が成り立ちます。
\(ma_B=-μ’N_B\)
なお\(N_B=mg\)なので、以下のように変形できます。
\(ma_B=-μ’mg\)
\(a_B=-μ’g\)
次に初速度\(v_0\)と等加速度直線運動の公式を利用することで静止後の板Bの速度\(v_B\)を計算しましょう。
\(v_B=v_0+a_Bt\)
\(v_B=v_0-μ’gt\)
こうして、板Bの速度を得ることができました。
次に板Aに着目しましょう。板Aに加わる力は、板Bからの摩擦力のみです。これにより、板Aの速度は徐々に上昇していきます。そこで板Aの加速度を\(a_A\)とすると、以下の運動方程式を作ることができます。
\(Ma_A=μ’N_B\)
\(N_B=mg\)なので、以下のように変形できます。
\(Ma_A=μ’mg\)
\(a_A=\displaystyle\frac{μ’mg}{M}\)
板Aは初速度0なので、等加速度直線運動の公式を利用することで以下のように板Aの速度\(v_A\)を表すことができます。
\(v_A=a_At\)
\(v_A=\displaystyle\frac{μ’mg}{M}t\)
なお板Bが静止した後では、\(v_A=v_B\)となります。そこで\(v_A=\displaystyle\frac{μ’mg}{M}t\)と\(v_B=v_0-μ’gt\)を利用し、経過時間\(t\)を計算しましょう。
\(v_A=v_B\)
\(\displaystyle\frac{μ’mg}{M}t=v_0-μ’gt\)
\(\displaystyle\frac{μ’mg}{M}t+μ’gt=v_0\)
\(μ’gt\left(\displaystyle\frac{m}{M}+1\right)=v_0\)
\(μ’gt\left(\displaystyle\frac{m+M}{M}\right)=v_0\)
\(t=\displaystyle\frac{Mv_0}{μ’g(m+M)}\)
こうして、\(\displaystyle\frac{Mv_0}{μ’g(m+M)}\)秒後に板Bが静止すると計算できました。
2) 板Bが静止した後、両物体の速さ\(v\)はいくらですか
\(t=\displaystyle\frac{Mv_0}{μ’g(m+M)}\)とわかっているため、\(v_A=\displaystyle\frac{μ’mg}{M}t\)に代入しましょう。\(\displaystyle\frac{Mv_0}{μ’g(m+M)}\)秒後では、\(v_A=v_B\)になるとわかっています。
\(v_A=\displaystyle\frac{μ’mg}{M}t\)
\(v_A=\displaystyle\frac{μ’mg}{M}×\displaystyle\frac{Mv_0}{μ’g(m+M)}\)
\(v_A=\displaystyle\frac{mv_0}{m+M}\)
板Bが静止した後、両物体の速度は\(=\displaystyle\frac{mv_0}{m+M}\)です。なお、\(v_B=v_0-μ’gt\)に\(t=\displaystyle\frac{Mv_0}{μ’g(m+M)}\)を代入することで答えを得ることもできます。
摩擦力の概念を理解し、計算できるようにする
重さのある物体を床に置く場合、通常は摩擦力が発生します。そこで、摩擦力を考慮して力のつり合いや運動方程式を考えるようにしましょう。
摩擦力には静止摩擦力と動摩擦力があります。また最大の静止摩擦力を最大摩擦力と呼び、静止摩擦係数と垂直抗力を利用して最大摩擦力を計算できます。一方で物体が動いているときの摩擦力が動摩擦力であり、動摩擦係数と垂直抗力を利用して動摩擦係数を計算できます。
作用・反作用の法則により、力の向きとは反対方向に摩擦力が働きます。そこで、摩擦力の向き(ベクトル)を判断できるようになりましょう。なお2物体の摩擦力は応用問題であり、計算の難易度が高くなります。そこで、それぞれの摩擦力や速度を計算できるようになりましょう。
力学で摩擦力を考慮する場合、計算が複雑になります。そこで摩擦力の向きや摩擦力の大きさを考え、正しく計算できるようになりましょう。






