私たちは電場を見ることができません。ただ物理では、実際には目に見えないものの、直線や曲線を利用することによって可視化することがひんぱんにあります。そこで、電場についても直線と曲線を利用して表しましょう。
電場を線によって表現する方法に電気力線があります。何本の線を記すのかによって、電場の強さ(大きさ)を表すことができます。
また、電気力線の数を計算する方法にガウスの法則があります。ガウスの法則を利用すれば、球だけでなくあらゆる物体の電気力線を計算できます。
それでは、電気力線の特徴には何があるのでしょうか。また、どのようにガウスの法則を利用して電気力線の数を出せばいいのでしょうか。電気力線とガウスの法則について解説していきます。
もくじ
電気力線とは何か:密度は電場の強さを表す
まず、電気力線とは何なのでしょうか。電場を可視化するために直線または曲線を利用し、引いた線を電気力線といいます。例えばプラスとマイナスの点電荷を置く場合、以下のように電気力線を記すことができます。
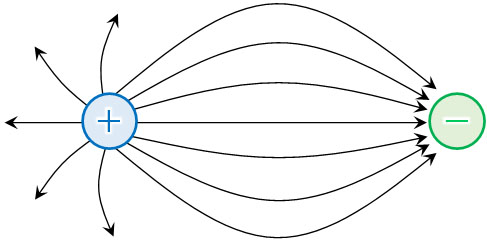
電場は目に見えませんが、物理現象を理解するとき、可視化することでわかりやすくなります。
電気力線の数は電場の強さを表しています。つまり強い電場がある場合、電気力線の本数(密度)が多くなります。一方で電場が弱い場合、電気力線の本数は少なくなります。
電気力線の書き方・ルール
それでは、電気力線を利用するときの書き方やルールには何があるのでしょうか。電場の強さと電気力線の本数が比例することは先ほど述べました。
他にも、電気力線には以下のルールがあります。
- 電気力線は正電荷から出て、負電荷に入る(または無限遠へ伸びる)
- 電気力線は折れ曲がりや枝分かれ、交わりがない
- 電場の方向は電気力線の接線方向
電気力線が発生するためには、必ず正電荷が必要です。理由なしに電気力線が生じることはありません。また正電荷から発生した電気力線は負電荷に入ることで消滅します。なお負電荷が周囲にない場合、電気力線は無限遠(無限に遠い場所)へ伸びていきます。
また、電気力線は途中で折れ曲がりや枝分かれ、交わりがありません。すべての電気力線は直線または曲線です。

電場の方向については、電気力線の接線を利用しましょう。電場では大きさと向き(ベクトル)が重要になります。そこでベクトルを得るとき、電気力線に対して接線を引くのです。
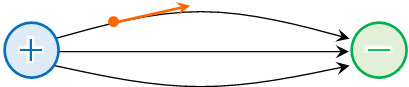
こうして、電気力線を利用することによって電場の向きがわかります。
ガウスの法則と電気力線の本数
それでは、電気力線は何本記せばいいのでしょうか。電気力線の本数によって電場の大きさを表すことができるため、自由に電気力線を記してはいけません。
電荷をもつ物体について、電気力線を何本書けばいいのか計算するときに用いるのがガウスの法則です。そこで、電気力線を記すときのルールを学びましょう。電気力線を記すとき、以下のルールがあります。
- 電場の大きさが\(E\)の場合、1m2に\(E\)[本]の電気力線を書くことができる
例えば電場の大きさが5N/Cであり、面積が3m2の場合は何本の電気力線を引くことができるでしょうか。電場の大きさが5N/Cの場合、1m2に5本の電気力線を引くことができます。そのため、3m2では15本の電気力線を引くことができます。
球の表面積と電場をかけると公式を得られる
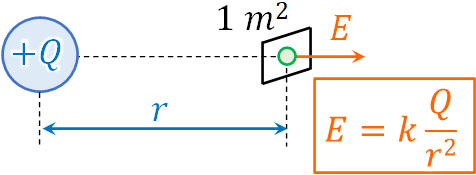
それでは、点電荷から発せられている電気力線の本数は何本でしょうか。点電荷の場合、点電荷からの距離によって電場の大きさが異なります。
点電荷の電気量が\(Q\)[C]、点電荷からの距離が\(r\)[m]の場合、電場の大きさが\(E=k\displaystyle\frac{Q}{r^2}\)[N/C]になることは既に知っていると思います。つまり点電荷からの距離が\(r\)[m]の場合、1m2当たり\(k\displaystyle\frac{Q}{r^2}\)[本]の電気力線を書くことができます。
次に、点電荷を中心にして、半径\(r\)[m]の球を作りましょう。球の表面積を計算する公式は数学で既に学んでいると思います。球の表面積は\(4πr^2\)[m2]です。
1m2に\(k\displaystyle\frac{Q}{r^2}\)[本]の電気力線が存在します。そのため\(4πr^2\)[m2]に存在する電気力線を知るためには、かけ算をすればいいとわかります。
\(k\displaystyle\frac{Q}{r^2}×4πr^2=4πkQ\)
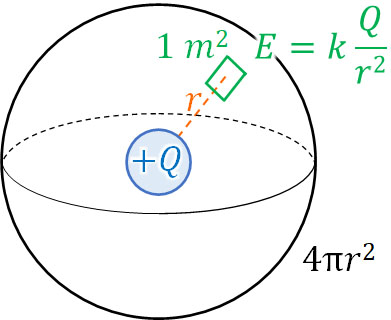
こうして、電気量\(Q\)[C]の点電荷から発せられる電気力線の本数は\(4πkQ\)とわかります。公式を覚える必要はなく、円の表面積を得る公式と電場の大きさを得る公式をかけることで公式を作れるようにしましょう。
ガウスの法則を利用し、平面電場を求める
ガウスの法則で重要なのは、球だけでなく、棒や平面などでも適用できることです。つまり、電気量\(Q\)[C]の物体から出る電気力線の合計本数\(N\)は形状に関係なく\(N=4πkQ\)となります。この知識はコンデンサーを学ぶときに役立ちます。
すべての形状でガウスの法則を利用できる事実を知ることは重要です。それでは金属板を用いて、平面電荷の電場の大きさを計算してみましょう。以下の問題の答えは何でしょうか。
- 面積\(S\)[m2]の金属板が電気量\(Q\)[C]にて一様に帯電しているとき、金属板の電場の大きさを求めましょう(\(Q>0\))。なお電気力線は金属表面から垂直に出ており、クーロン定数は\(k\)です。
球の場合、全方向に対して電気力線が出ます。一方で金属板の場合、平面なので上下の2方向に対して垂直に電気力線が発せられます。
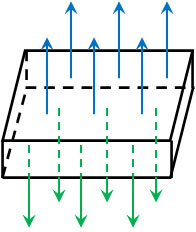
ガウスの法則より、この金属板から発せられる電気力線の総数は\(4πkQ\)です。
先ほど、ガウスの法則の公式を得るとき、電場\(E\)と面積をかけることによって電気力線の総数を計算しました。今回は電気力線の総数がわかっているため、電気力線の総数に対して面積\(S\)で割りましょう。これにより、電場\(E\)を得ることができます。
金属板の面積は\(S\)[m2]であるため、上下両方の面積を合わせると\(2S\)[m2]です。そのため、以下の式によって電場\(E\)を得ることができます。
\(E=\displaystyle\frac{4πkQ}{2S}=\displaystyle\frac{2πkQ}{S}\)
こうして、金属板の電荷は\(E=\displaystyle\frac{2πkQ}{S}\)とわかりました。
電気力線の定義を利用することにより、電場\(E\)を計算できます。具体的には、物体がもつ電気力線の総本数は\(4πkQ\)であるため、物体の表面積\(S\)がわかれば、電場\(E\)がわかるのです。
ガウスの法則を利用し、電気力線の本数を得る
電気力線を学ぶことにより、電場を可視化できます。電気力線の書き方にはルールがあるため、どのように電気力線を描けばいいのか理解しましょう。
電場\(E\)では、1m2当たり\(E\)[本]の電気力線を書くことができます。そのため点電荷では、球の表面積が\(4πr^2\)であるため、電気力線の合計本数は\(4πkQ\)となります。ガウスの法則を暗記するのではなく、公式の導き出し方を学びましょう。
またガウスの法則は球だけでなく、あらゆる物体で利用できます。棒や板であってもガウスの法則を利用できるため、面積がわかれば電場\(E\)の計算が可能です。
ガウスの法則は点電荷と平面電荷を学ぶ基礎となります。そこで電気力線とガウスの法則を理解しましょう。






