レンズの公式：凸レンズ、凹レンズの性質

私たちは多くの場面でレンズを利用します。カメラや眼鏡など、日常生活でレンズが利用される場面は非常に多いです。

それでは、なぜレンズは物体を拡大させることができるのでしょうか。また、レンズを利用することによってなぜ近視を改善させることができるのでしょうか。

レンズには凸レンズと凹レンズがあります。凸レンズと凹レンズは性質が大きく異なるため、役割も違います。なおレンズの公式は基本的に同じであるものの、凸レンズと凹レンズでは公式を利用するときに符号が変化します。

そこで、レンズを利用することで物体を拡大または縮小させるとき、どのような原理になっているのかを学びましょう。ここではレンズの性質や公式の意味を解説していきます。

1 レンズの性質：光軸と焦点
- 1.1 凸レンズの3つの性質：実像と虚像の違い
  - 1.1.1 物体が焦点の外側にある場合の像：実像
  - 1.1.2 物体が焦点の内側に存在する場合の像：虚像
- 1.2 凹レンズの性質と虚像
  - 1.2.1 凹レンズでは、レンズの手前に虚像ができる
2 レンズの公式：凸レンズで実像または虚像を得るときの公式
3 凸レンズと凹レンズの性質を学び、レンズの公式を利用する

レンズの性質：光軸と焦点

まず、レンズとは何でしょうか。通常、光は直進します。しかしレンズを通ると、光は曲がります。光の屈折を利用することにより、光の進行方向を変える性質をもつ道具がレンズです。

なお、ガラスであっても光を屈折させます。光を屈折させる道具の中でも、特定の点から発せられた光が屈折し、ある一点に集まるように設計された道具がレンズです。例えば以下のように、点Aから発せられた光がレンズを通ると、屈折することによって点A’に集まります。

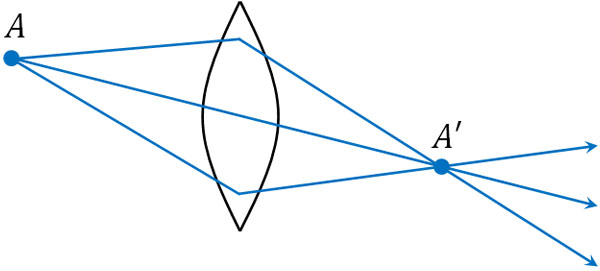
屈折によって点A’に光が集まることにより、点A’にも光源があるように見えてしまいます。本来は点Aに存在する物体であっても、点A’に存在するように見えるのです。

なおレンズの中心を通り、レンズに垂直な直線を光軸といいます。下図のように、光がレンズの光軸に対して平行に入射すると、必ず光軸上の一点に集まります。この点を焦点といいます。焦点はレンズの左右に一つずつ存在します。

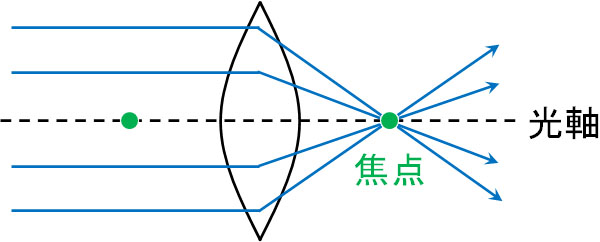
レンズを学ぶためには、これらの用語と性質を理解しなければいけません。なおレンズから焦点までの距離については、レンズの形状（厚み、曲がり具合）や材質によって異なります。

凸レンズの3つの性質：実像と虚像の違い

それでは、レンズの性質を確認しましょう。レンズには凸レンズと凹レンズがあります。中央が膨らんでいるレンズが凸レンズです。虫眼鏡や眼球の水晶体が凸レンズに該当します。

凸レンズには光を集める性質があります。このとき、凸レンズには以下の3つの性質があることを覚えましょう。

・光がレンズの中心を通る場合、直進する

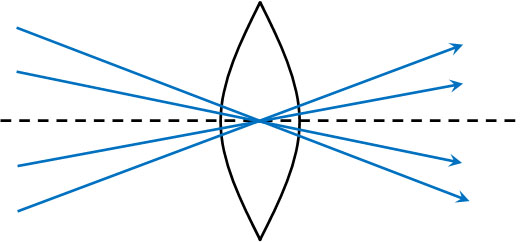
通常、レンズを通ると光は屈折します。ただ光がレンズの中心を通る場合、例外的に光は屈折せずに直進します。

・光軸と平行に入射した光はレンズを通過後、焦点を通る

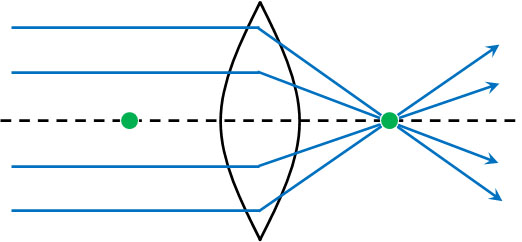
レンズの光軸に対して平行に入射する光は必ず焦点に集まります。

凸レンズを利用すると、太陽の光が焦点に集まります。これによって高熱となり、物体を焦がすことができます。虫眼鏡を利用して太陽を見てはいけないのは、目が焦げてしまうからです。

・焦点を通る光はレンズを通過後、光軸に対して平行に進む

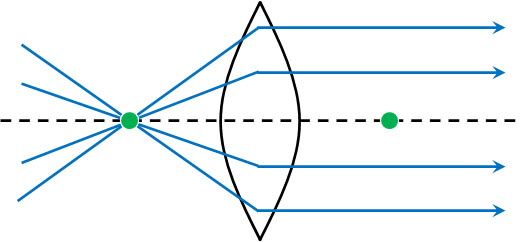
光軸に対して平行に入射した光が焦点に集まるというのは、「焦点を通過した光がレンズを通過すると、光軸に対して平行に進む」ことを意味しています。

これら凸レンズの性質を利用することによって、凸レンズのどの位置に物体の像を生じるのかわかるようになります。

物体が焦点の外側にある場合の像：実像

それでは物体が焦点の外側にある場合、どのような像ができるのか確認しましょう。焦点の外側に物体を置き、以下の光線を図示します。

レンズの中心を通る光
レンズに対して平行な光
レンズの焦点を通る光

そうすると、以下の図となります。

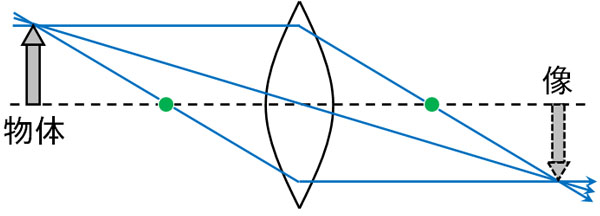
こうして、上下逆さまの像（倒立像）を得られます。このとき得られる像は光が集まることによって生じているため、実像と呼ばれます。

虫眼鏡を利用して遠くの物体を見ると、上下逆さまになります。この理由として、遠くにある物体がレンズを通ってあなたの目に届くとき、光が上下逆さまになるからです。

なお実際には、光が反射することで物体からは無数の光が発せられています。このとき、代表的な光を利用すれば実像の場所がわかります。そこで、先ほど解説した3つの光（または先ほど解説した光のうち2つ）を利用して記すのが一般的な方法です。

物体が焦点の内側に存在する場合の像：虚像

一方で物体が焦点の内側に存在する場合はどのような像になるのでしょうか。虫眼鏡（凸レンズ）を利用する理由としては、多くの場合で小さい物体を拡大したいからです。上下逆さまに物体を見たいという理由から虫眼鏡を利用するわけではありません。

そこで、物体を焦点の内側に置きましょう。虫眼鏡を物体に近づけると、物体が拡大される現象は多くの人が知っています。

それでは、なぜ通常の大きさよりも拡大されるのでしょうか。物体を凸レンズの焦点よりも内側に置く場面を考えてみましょう。

この場合、先ほどと同じように3本の光を利用すると、レンズの後方で像を作ることはできません。そこで、下図のように3本の光をレンズの前方（左側）に伸ばしましょう。

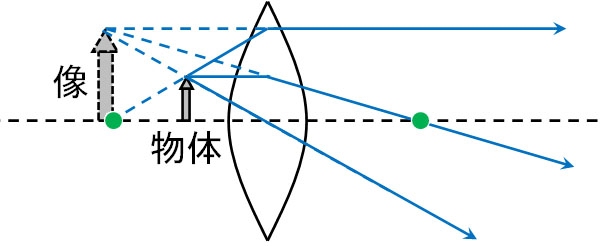
このように図を作ると、物体の左側に像を作れます。本来、像の位置に物体は存在しないものの、レンズの右側からあなたが物体を見ると、像の場所に物体が存在しているように見えるのです。また、像は物体よりも大きくなります（正立虚像）。

これが、虫眼鏡を物体に近づけると拡大される理由です。今回の例の場合、レンズの右側から物体を見ると、像が作られる場所に光が集まっているように見えるのです。

なお焦点の内側に物体を置くとき、実際に光が集まって像が作られているわけではありません。このような像を虚像といいます。

実像では光が集まっているため、スクリーンを置くと上下逆さまの像が写ります。一方で虚像では光が集まっているわけではないため、実像とは異なり、スクリーンを用意しても映りません。虚像はレンズを通して見ることによってのみ確認できるのです。

凹レンズの性質と虚像

凸レンズとは異なり、光を発散する性質をもつ道具が凹レンズです。近視用の眼鏡は凹レンズが利用されています。

先ほど、レンズでは「光軸に対して平行に入射する光が集まる点（焦点）が存在する」と解説しました。凸レンズでは、光がレンズを通過後に焦点を通ります。一方で凹レンズでは、光がレンズを通過後、光は手前の焦点を通過した場合と同じ向きになります。

それでは、図を利用して凹レンズに存在する3つの性質を確認しましょう。

・レンズの中心を通る光は直進する

凸レンズと同様に、レンズの中心を通る光は直進します。

・光軸と平行に入射した光は、レンズ手前の焦点を通過したように進む

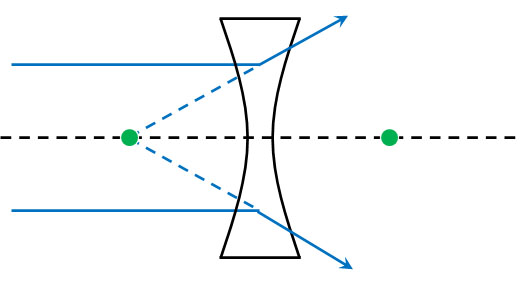
凸レンズとは反対の性質をもつのが凹レンズです。凸レンズでは、光軸に対して平行に入射した光は焦点を通ります。一方で凹レンズでは、平行に入射した光は「レンズ手前の焦点を通ったように進む」ことになります。

・焦点に向かって進む光は、レンズを通過後に光軸に対して平行に進む

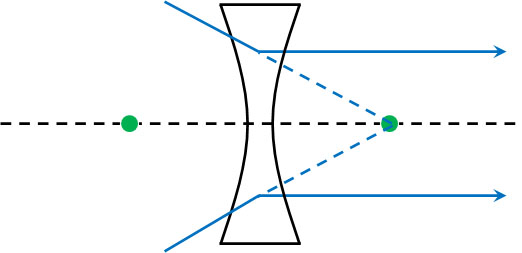
先ほどとは反対の現象が起こります。焦点に向かって進む光が凹レンズを通過すると、光は平行に進みます。

凹レンズでは、レンズの手前に虚像ができる

これらの性質があるため、凹レンズを利用すると、レンズの手前に虚像を作ることができます。

凸レンズでは、焦点の手前に物体を置くことにより、拡大された虚像を作ることができました。凹レンズを利用する場合、これと反対の現象が起こります。つまり拡大された正立虚像ではなく、凹レンズでは縮小された正立虚像が作られます。

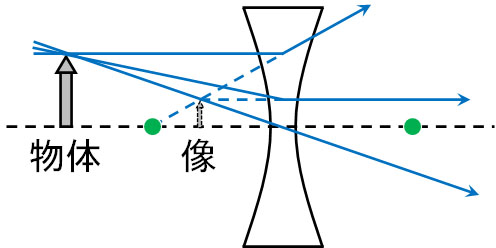
注意点として、焦点の位置に関係なく縮小された正立虚像が作られます。凸レンズでは、物体が焦点の外側にあるのか、それとも内側にあるのかが重要です。物体の位置によって正立虚像を作ることができたり、倒立実像を作ることができたりします。

一方で凹レンズについては、焦点の外側に物体があっても、焦点の内側に物体があっても、作られる像は正立虚像です。

レンズの公式：凸レンズで実像または虚像を得るときの公式

ここまでの内容を理解したら、レンズの公式を学びましょう。レンズを利用することによって作られる像の距離や大きさ（倍率）を計算できるようにするのです。そこで、レンズの公式を学びましょう。

三角形の相似を利用することにより、レンズの公式を導出できます。以下がレンズの公式です（物体とレンズとの距離を\(a\)、レンズと像との距離を\(b\)、焦点距離を\(f\)とします）。

\(\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b}=\displaystyle\frac{1}{f}\)

それでは、なぜこの公式が成り立つのか確認しましょう。

・凸レンズで倒立実像を得るときの公式

まず、凸レンズで得られる倒立実像の公式を導き出しましょう。方法は難しくなく、焦点の外側に物体を置いている以下の図を作ります。

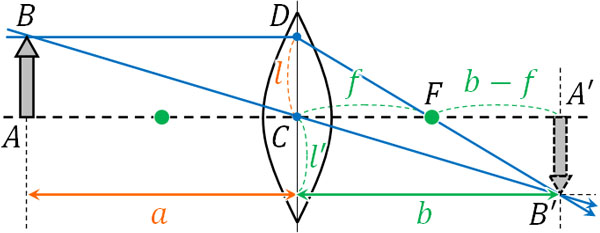
上図について、△ABCと△A’B’Cは相似です。そのため、\(l:l’=a:b\)です。また△CDFと△A’B’Fは相似です。そのため、\(l:l’=f:(b-f)\)です。

\(l:l’=a:b\)と\(l:l’=f:(b-f)\)より、\(a:b=f:(b-f)\)です。つまり、以下のように計算できます。

\(a:b=f:(b-f)\)

\(bf=a(b-f)\)

\(\displaystyle\frac{b}{a}=\displaystyle\frac{b-f}{f}\)

\(\displaystyle\frac{1}{a}=\displaystyle\frac{b-f}{bf}\)

\(\displaystyle\frac{1}{a}=\displaystyle\frac{1}{f}-\displaystyle\frac{1}{b}\)

\(\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b}=\displaystyle\frac{1}{f}\)

こうして、レンズの公式を得ることができました。

・凸レンズで正立虚像を得るときの公式

次に、凸レンズを利用して正立虚像を得るときの公式を導き出しましょう。方法は先ほどと同じであり、焦点の内側に物体を置いている以下の図を作ります。

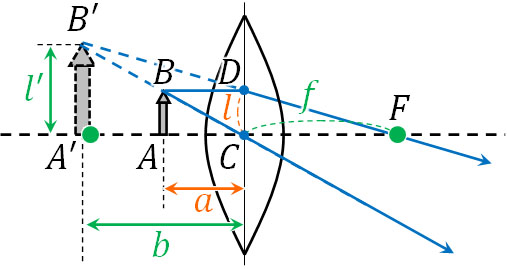
上図について、△ABCと△A’B’Cは相似です。そのため、\(l:l’=a:b\)です。また△CDFと△A’B’Fは相似です。そのため、\(l:l’=f:(b+f)\)です。

\(l:l’=a:b\)と\(l:l’=f:(b+f)\)より、\(a:b=f:(b+f)\)です。つまり、以下のように計算できます。

\(a:b=f:(b+f)\)

\(bf=a(b+f)\)

\(\displaystyle\frac{b}{a}=\displaystyle\frac{b+f}{f}\)

\(\displaystyle\frac{1}{a}=\displaystyle\frac{b+f}{bf}\)

\(\displaystyle\frac{1}{a}=\displaystyle\frac{1}{f}+\displaystyle\frac{1}{b}\)

\(\displaystyle\frac{1}{a}-\displaystyle\frac{1}{b}=\displaystyle\frac{1}{f}\)

凸レンズで焦点の外側に物体を置く場合とは異なり、内側に物体を置くと物体と同じ側に虚像ができます。そのため物体を焦点の内側に置く場合、レンズの公式では\(b\)が\(-b\)へ変化します。

凹レンズを利用するときのレンズの公式

それでは、凹レンズを利用するときのレンズの公式はどのようになるのでしょうか。以下の図を作り、三角形の相似を比べましょう。

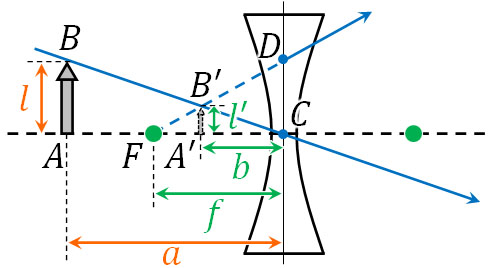
上図について、△ABCと△A’B’Cは相似です。そのため、\(l:l’=a:b\)です。また△CDFと△A’B’Fは相似です。そのため、\(l:l’=f:(f-b)\)です。

\(l:l’=a:b\)と\(l:l’=f:(f-b)\)より、\(a:b=f:(f-b)\)です。つまり、以下のように計算できます。

\(a:b=f:(f-b)\)

\(bf=a(f-b)\)

\(\displaystyle\frac{b}{a}=\displaystyle\frac{f-b}{f}\)

\(\displaystyle\frac{1}{a}=\displaystyle\frac{f-b}{bf}\)

\(\displaystyle\frac{1}{a}=\displaystyle\frac{1}{b}-\displaystyle\frac{1}{f}\)

\(\displaystyle\frac{1}{a}-\displaystyle\frac{1}{b}=-\displaystyle\frac{1}{f}\)

こうして、凹レンズでのレンズの公式を得ることができました。

レンズ公式と倍率の計算

レンズの公式を確認すると、すべてにおいて以下の公式であることがわかります。

\(\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b}=\displaystyle\frac{1}{f}\)

ただ凸レンズで正立虚像の場合、\(b<0\)となるため、\(b\)の符号はマイナスになります。また凸レンズの場合は\(f>0\)となり、凹レンズの場合は\(f<0\)となります。

・三角形の相似を利用し、倍率を計算する

このとき、三角形の相似を利用すれば倍率の計算が可能です。三角形の相似より、下図で\(l:l’=a:b\)です。

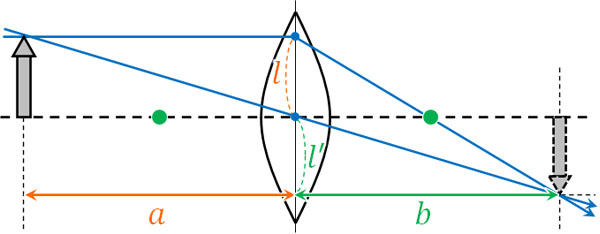
そのため、以下が成り立ちます。

\(\displaystyle\frac{l’}{l}=\left|\displaystyle\frac{b}{a}\right|\)

この式を利用することにより、作られる像の長さが物体の何倍になるのかを表すことができます。\(a\)と\(b\)の長さを利用することで倍率の計算が可能なのです。

凸レンズと凹レンズでの練習問題

それでは、レンズの公式を利用して問題を解いてみましょう。以下の問題の答えは何でしょうか。

焦点距離が10cmの凸レンズがあります。凸レンズから15cm離れた場所に長さ3cmの棒を立てました。

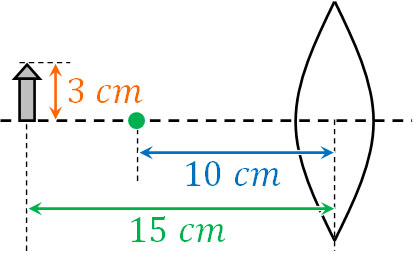
凸レンズによってできる像の長さを求めましょう。
レンズを焦点距離30cmの凹レンズに変える場合、できる像の位置を求めましょう。

1) 凸レンズによってできる像の長さを求めましょう

棒は焦点の外側に存在するため、凸レンズを利用することによって倒立実像ができます。そこで、レンズの公式を利用して\(b\)を計算しましょう。

\(\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b}=\displaystyle\frac{1}{f}\)

\(\displaystyle\frac{1}{15}+\displaystyle\frac{1}{b}=\displaystyle\frac{1}{10}\)

\(\displaystyle\frac{1}{b}=\displaystyle\frac{3}{30}-\displaystyle\frac{2}{30}\)

\(\displaystyle\frac{1}{b}=\displaystyle\frac{1}{30}\)

\(b=30\)

\(b=30\)なので、倍率は\(\left|\displaystyle\frac{30}{15}\right|=2\)倍です。そのため、像の長さは6cmです。

2) レンズを焦点距離30cmの凹レンズに変える場合、できる像の位置を求めましょう

凹レンズを利用するため、先ほどの公式について、\(f\)をマイナスにして値を代入しましょう。

\(\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b}=-\displaystyle\frac{1}{f}\)

\(\displaystyle\frac{1}{15}+\displaystyle\frac{1}{b}=-\displaystyle\frac{1}{30}\)

\(\displaystyle\frac{1}{b}=-\displaystyle\frac{1}{30}-\displaystyle\frac{1}{15}\)

\(\displaystyle\frac{1}{b}=-\displaystyle\frac{3}{30}\)

\(\displaystyle\frac{1}{b}=-\displaystyle\frac{1}{10}\)

\(b=-10\)

こうして、レンズの手前10cmの場所（棒から5cm、レンズに近い場所）に正立虚像ができると計算できました。

なお計算するとき、\(\displaystyle\frac{1}{a}-\displaystyle\frac{1}{b}=-\displaystyle\frac{1}{f}\)を利用することもできます。この場合は\(b=10\)を得ることができます。\(b=\)をマイナスにして計算しているため、\(\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b}=-\displaystyle\frac{1}{f}\)を利用した場合と同様に、レンズの手前10cmの場所に正立虚像ができると判断しましょう。