平方根の足し算と引き算：ルート計算のやり方や分数の求め方

中学数学で習う分野が平方根です。根号（ルート）を使うことで、2乗する前の数字を表せるようになります。

平方根の計算では、足し算と引き算があります。掛け算と割り算については、ルート内の数字をそのまま掛け算すればいいです。一方で足し算と引き算では、ルート内の数字が同じでなければ計算してはいけないというルールがあります。

また足し算と引き算では、素因数分解や分母の有理化を行う必要があります。平方根の計算では、掛け算よりも足し算と引き算の内容のほうが難しくなっています。

そこで、どのようにして平方根の足し算と引き算をすればいいのかについて、ルート計算のやり方を解説していきます。

根号（ルート）の足し算・引き算のやり方

平方根の掛け算と割り算では、ルート同士の掛け算をすればいいです。注意点はあるものの、ルート記号をもつ数字を掛けるだけです。

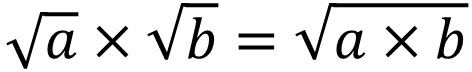
一方で足し算と引き算はどのように考えればいいのでしょうか。足し算と引き算については、数字が異なるルート同士の足し算や引き算をしてはいけません。例えば、以下は間違いです。

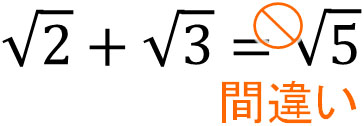
掛け算・割り算とは、計算方法が異なります。なぜ、異なる数字のルート同士で足し算をしてはいけないのでしょうか。2乗する前の数字なので、整数とは性質が異なるからです。

例えば、\(\sqrt{9}=\sqrt{3^2}=3\)です。また\(\sqrt{16}=\sqrt{4^2}=4\)です。つまり、以下のようになります。

• \(\sqrt{9}+\sqrt{16}=3+4=7\)

一方で整数にせずにルート同士の足し算をすればどうなるでしょうか。以下のようになります。

• \(\sqrt{9}+\sqrt{16}=\color{red}{\sqrt{9+16}}=\sqrt{25}\)

5²は25です。そのため、\(\sqrt{25}=\sqrt{5^2}=5\)になります。ただ、本当の答えは7にならなければいけません。つまり、\(\sqrt{9}+\sqrt{16}=\sqrt{25}=5\)は間違いです。

2乗の数字がルートなので、以下のようになります。

• \(\sqrt{36}=6\)
• \(\sqrt{100}=10\)
• \(\sqrt{2500}=50\)
• \(\sqrt{10000}=100\)

このように、整数に比べてルート内の数字は非常に大きい数字になります。整数（自然数）とルート内の数字はまったくの別物だと考えるようにしましょう。これが、根号の中の数字に対して、そのまま足し算や引き算をすると間違いになる理由です。

ルート内の数字が同じだと足し算・引き算できる

それでは、平方根ではどのように足し算と引き算をすればいいのでしょうか。やり方としては、ルート内の数字が同じ場合のみ、足し算と引き算できます。例えば、以下のようになります。

• \(4\sqrt{2}-\sqrt{2}=3\sqrt{2}\)

この場合、ルート内の数字は2と共通しています。そのため、ルート記号の前にある整数の足し算・引き算が可能です。

\(4\sqrt{2}\)とは、\(\sqrt{2}\)が4つある状態を指します。そこで\(\sqrt{2}\)を一つ引くと、\(\sqrt{2}\)は3つ残ります。

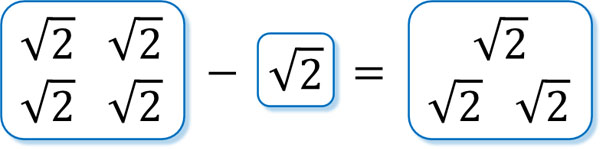
これが、根号の中の数字が同じ場合は足し算・引き算が可能な理由です。

一方でルート内の数字が違う場合はどうなるのでしょうか。既に説明した通り、ルート内の数字が同じ場合は足し算・引き算が可能です。しかし、ルート内の数字が違う場合は足し算・引き算をしてはいけません。例えば、以下のように計算します。

• \(2\sqrt{\color{red}{2}}-\sqrt{3}+3\sqrt{\color{red}{2}}=5\sqrt{2}-\sqrt{3}\)

性質が異なる数字の足し算・引き算はできません。そのため、この計算は\(5\sqrt{2}-\sqrt{3}\)が答えです。足し算・引き算が可能かどうかは、ルート内の数字が同じかどうかで判断しましょう。

・計算方法は文字式（代数式）と同じ

ルートの計算は文字式（代数式）とやり方が同じです。文字式では、異なる文字であっても掛け算・割り算が可能です。ただ、以下のように異なる文字の足し算・引き算はできません。

• \(2x+x-2y+4y=3x+2y\)

平方根については、ルート内の数字が違っていたとしても掛け算・割り算が可能です。しかしルート内の数字が異なる場合、以下のように足し算・引き算はできません。

• \(2\sqrt{\color{red}{2}}+\sqrt{\color{red}{2}}-2\sqrt{\color{blue}{3}}+4\sqrt{\color{blue}{3}}=3\sqrt{2}+2\sqrt{3}\)

性質が違っていたとしても、掛け算やわり算は可能です。しかし性質が違うと、足し算・引き算はできません。数学では、このルールを理解するようにしましょう。

素因数分解によってルート内の数字を合わせる

ここまで説明したルールを理解すれば、平方根の足し算・引き算ができるようになります。ただ足し算・引き算をする前、多くのケースで事前に素因数分解をしなければいけません。素因数分解をすることで、ルート内の数字が明確になります。

平方根の計算をするとき、素因数分解によって\(a\sqrt{b}\)の形に直さなければいけません。例えば、以下のようになります。

\(\sqrt{18}+\sqrt{50}-\sqrt{32}\)

\(=\sqrt{3^2×2}+\sqrt{5^2×2}-\sqrt{4^2×2}\)

\(=3\sqrt{2}+5\sqrt{2}-4\sqrt{2}\)

\(=4\sqrt{2}\)

平方根の計算で素因数分解が重要なのは、ルート内の数字を最小にできるからです。その結果、足し算・引き算が可能になります。

分母の有理化をした後、通分して計算する

ルート計算をするとき、他に重要な手順があります。それが分母の有理化です。分母に平方根（無理数）があると、計算できません。そこで分母の有理化をすることで、分母の数を整数に変えれば、通分することによって平方根同士の足し算・引き算が可能になります。

例えば、以下の計算はどのようにすればいいのでしょうか。

• \(\displaystyle\frac{1}{\sqrt{3}}+\sqrt{3}\)

中学数学では、分母にルートがある状態だと不正解です。なぜかというと、分母の有理化をすることで数字をより簡潔にできるからです。

分母の有理化をする場合、以下のように計算できます。

\(\displaystyle\frac{1}{\sqrt{3}}+\sqrt{3}\)

\(=\displaystyle\frac{1\color{red}{×\sqrt{3}}}{\sqrt{3}\color{red}{×\sqrt{3}}}+\sqrt{3}\)

\(=\displaystyle\frac{\sqrt{3}}{3}+\sqrt{3}\)

\(=\displaystyle\frac{\sqrt{3}}{3}+\color{red}{\displaystyle\frac{3\sqrt{3}}{3}}\) （通分する）

\(=\displaystyle\frac{4\sqrt{3}}{3}\)

このように分母の有理化をすれば、通分によって足し算・引き算が可能になります。

分配法則を使う平方根の掛け算・割り算

なお実際にルート計算をするとき、足し算や引き算をするだけではありません。掛け算や割り算を含めた計算式になることが多いです。そのため足し算・引き算・掛け算・割り算のすべてが混じった式の計算を行えるようにしましょう。

前述の通り、文字式（代数式）とルートは計算方法が同じです。代数式で重要なルールに分配法則があります。以下が分配法則です。

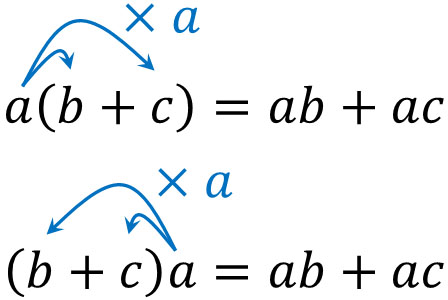
掛け算のかっこを外すための方法が分配法則です。ルート計算でも、分配法則を利用して計算するようにしましょう。

例えば、以下はどのように計算すればいいのでしょうか。

• \(2(1+\sqrt{2})\)

この問題を解くため、分配法則を利用しましょう。以下のようになります。

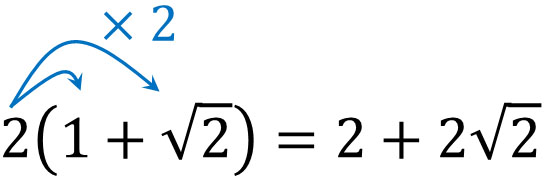
式の展開をした後、足し算や引き算をすることで計算を進めていくようにしましょう。

乗法公式を使って式の展開をする

ただ平方根の計算では、より複雑な式の計算をしなければいけません。乗法公式を利用することで、式の展開をするのです。

2つのかっこを用いた掛け算の式を展開するとき、以下の公式を利用します。

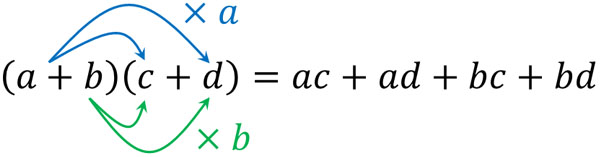
また、より効率的に計算するときは他の乗法公式も利用します。中学数学の計算では、以下の4つの公式を必ず覚えなければいけません。

• \((x+a)(x+b)=x^2+(a+b)x+ab\)
• \((x+a)^2=x^2+2ax+a^2\)
• \((x-a)^2=x^2-2ax+a^2\)
• \((x+a)(x-a)=x^2-a^2\)

この公式を利用することで、平方根の計算をします。例えば、以下の計算をどのようにすればいいのか考えてみましょう。

• \((3+\sqrt{5})^2\)

この計算をするためには、乗法公式を利用しなければいけません。求め方は以下のようになります。

\((3+\sqrt{5})^2\)

\(=3^2+2×3×\sqrt{5}+(\sqrt{5})^2\)

\(=9+6\sqrt{5}+5\)

\(=14+6\sqrt{5}\)

整数とルートは性質が異なります。そのため、14と\(6\sqrt{5}\)はそれ以上の計算ができません。そのため、計算はこれで完了です。平方根の性質を理解することで、どのように計算すればいいのか理解するようにしましょう。

練習問題：ルート計算の足し算と引き算

Q1. 次の計算をしましょう

1. \(\sqrt{75}+\sqrt{98}-\sqrt{108}\)
2. \(\sqrt{8}-\displaystyle\frac{1}{\sqrt{2}}\)
3. \(\sqrt{6}(\sqrt{2}-\sqrt{3})+3\sqrt{3}\)

A1. 解答

(a)

素因数分解をした後、ルート計算をしましょう。

\(\sqrt{75}+\sqrt{98}-\sqrt{108}\)

\(=5\sqrt{3}+7\sqrt{2}-6\sqrt{3}\)

\(=7\sqrt{2}-\sqrt{3}\)

(b)

分母の有理化をした後、ルート計算をしましょう。

\(\sqrt{8}-\displaystyle\frac{1}{\sqrt{2}}\)

\(=2\sqrt{2}-\displaystyle\frac{1\color{red}{×\sqrt{2}}}{\sqrt{2}\color{red}{×\sqrt{2}}}\)

\(=2\sqrt{2}-\displaystyle\frac{\sqrt{2}}{2}\)

\(=\displaystyle\frac{4\sqrt{2}}{2}-\displaystyle\frac{\sqrt{2}}{2}\)

\(=\displaystyle\frac{3\sqrt{2}}{2}\)

(c)

分配法則を利用して計算しましょう。

\(\sqrt{6}(\sqrt{2}-\sqrt{3})+3\sqrt{3}\)

\(=\sqrt{12}-\sqrt{18}+3\sqrt{3}\)

\(=2\sqrt{3}-3\sqrt{2}+3\sqrt{3}\)

\(=-3\sqrt{2}+5\sqrt{3}\)

Q2. 次の計算をしましょう

\(x=2+\sqrt{2}\)、\(y=4+2\sqrt{2}\)のとき、\(xy-2x^2\)の値を計算しましょう。

A2. 解答

\(x\)と\(y\)に対して、数字を代入して計算することができます。以下のようになります。

• \((2+\sqrt{2})(4+2\sqrt{2})-2(2+\sqrt{2})^2\)

ただ、計算が大変です。もっと簡単に計算する方法はないのでしょうか。そこで、因数分解を利用しましょう。\(xy-2x^2\)を因数分解すると、以下のようになります。

• \(xy-2x^2=x(y-2x)\)

その後、この式に代入します。以下のようになります。

\(x(y-2x)\)

\(=(2+\sqrt{2})[4+2\sqrt{2}-2(2+\sqrt{2})]\)

\(=(2+\sqrt{2})(4+2\sqrt{2}-4-2\sqrt{2})\)

\(=(2+\sqrt{2})×0\)

\(=0\)

中学数学で根号（ルート）の足し算・引き算を行う

平方根の基本を学ぶとき、掛け算と割り算を学んだあとは足し算と引き算を習います。ルート内の数字を足せばいいわけではなく、ルート計算にはルールがあります。

根号の足し算・引き算は文字式の計算と同じです。掛け算と割り算については、そのまま掛けることができます。一方で足し算と引き算の答えを求める場合、ルート内の数字が同じでなければいけません。性質が同じものでなければ、足し算・引き算をすることができないのです。

そこで素因数分解や分母の有理化をすることで、ルート内の数字を揃えるようにしましょう。またかっこを用いた掛け算の式では、乗法公式を利用するようにしましょう。

平方根を学ぶとき、最も難しい概念の一つが足し算と引き算です。「なぜ、根号の中の数字が同じでなければ足し算・引き算ができないのか」をよく理解したうえでルート計算するようにしましょう。