平方根とルート（根号）の概念：有理数と無理数の違い

中学数学で学ぶ重要な分野に平方根があります。数学では累乗の計算をします。2乗や3乗をすることで、数字の掛け算をします。平方根は累乗の親戚です。累乗の概念を学んでいる場合、平方根を理解できます。

また平方根では、ルートという記号を使います。ルートを使う数字では、\(\sqrt{2}\)などのように表します。平方根を勉強した後では、ルートを用いた数字が非常に多く出てきます。

それでは、平方根はどのような概念なのでしょうか。また、どのようにルートを使えばいいのでしょうか。平方根と累乗はどのような関係があるのでしょうか。

なお数字には有理数と無理数があります。ルートが付く数字は無理数に分類されます。多くの場合、ルートを習うときに無理数の概念を学びます。これらの定義を含めて、平方根の概念を説明していきます。

1 平方根とは何か：2乗の数の考え方
2 有理数と無理数：整数、有限小数、循環小数は有理数
- 2.1 円周率やルートは無理数
3 練習問題：平方根の計算
4 平方根の定義とルートの概念を理解する

平方根とは何か：2乗の数の考え方

まず、平方根とは何でしょうか。数学では累乗を学びます。例えば、4²は\(4×4=16\)です。また、4³は\(4×4×4=64\)です。累乗は掛け算と意味が同じです。

一方で数学では、累乗の逆があります。平方根とは、ザックリと「累乗の逆」と理解しましょう。2乗することで特定の数になる場合、平方根といいます。

4²の答えは前述の通り16です。では、16の平方根は何でしょうか。16は4²のため、16の平方根は4です。平方根とは、2乗の逆と理解しましょう。

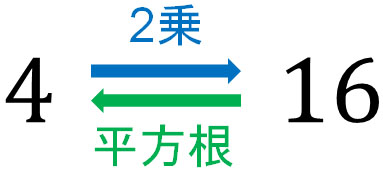
ただ、平方根では答えが2つあることに注意が必要です。2乗の計算では、答えは一つです。一方で平方根では、答えが1つではないのです。

2乗することで16になる数字として、何があるでしょうか。前述の通り、4を2乗すると16です。ただ、-4を2乗しても16になります。(-4)²の答えは16です。つまり、16の平方根は4と-4です。平方根では、2つ答えがあることを理解しましょう。

ルート（根号）の使い方

平方根はどのように表せばいいのでしょうか。平方根は根号（ルート）を使います。例えば、16の平方根をどのように表せばいいのでしょうか。16の平方根を表したい場合、数学では\(\sqrt{16}\)と記します。2乗することで16になる場合、\(\sqrt{16}\)となります。

ただ、16は4²のです。そのため、以下のように根号を外すことができます。

\(\sqrt{16}=\sqrt{4^2}=4\)

同じように考えると、\(\sqrt{25}\)の答えは5です。\(\sqrt{100}\)の答えは10です。根号（ルート）を外すことで、2乗する前の数字を表せます。

\(\sqrt{25}=\sqrt{5^2}=5\)
\(\sqrt{100}=\sqrt{10^2}=10\)

・2乗できない数字はどうするのか

ただ、2乗できない数字は非常に多いです。例えば36は6²なので、\(\sqrt{36}\)の答えは6になると分かります。一方で2や3の平方根は何でしょうか。

先ほど、2乗する前の数字について、根号を使って表記すると述べました。同じように、2や3の数についても、ルートを使うことで平方根を表すことができます。つまり、2の平方根は\(\sqrt{2}\)と\(-\sqrt{2}\)です。

平方根を表すとき、必ず根号を使うようにしましょう。例えば、11の平方根は\(\sqrt{11}\)と\(-\sqrt{11}\)です。また、15の平方根は\(\sqrt{15}\)と\(-\sqrt{15}\)です。ルートを使えば、平方根を表せるようになります。

・2乗すれば必ずルートが外れる

なお、2乗する前の数字がルートです。そのため根号を2乗すると、必ずルートが外れます。例えば、以下のようになります。

\((\sqrt{5})^2=5\)
\((\sqrt{11})^2=11\)

ルートを正の数と負の数で表す

ただ前述の通り、平方根には2つ答えが存在します。しかし数学では、正の数と負の数は性質が反対です。そのため、プラスなのかマイナスなのか明確に区別しなければいけません。

そこで平方根のうち、正の数を\(\sqrt{a}\)と表します。一方で負の数を\(-\sqrt{a}\)と表します。例えば、2の平方根は\(\sqrt{2}\)と\(-\sqrt{2}\)です。

なぜ、2の平方根を\(-\sqrt{2}\)と表せるのでしょうか。それはマイナスとマイナスの掛け算をすると、プラスになるからです。以下のようになります。

\((-\sqrt{2})^2=2\)

つまり平方根では、以下のように記すルールがあります。

プラスの平方根：\(\sqrt{a}\)
マイナスの平方根：\(-\sqrt{a}\)

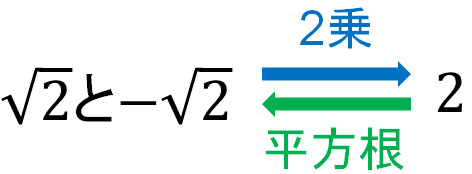
平方根には2つの答えがあります。そこでルートで答えを記すとき、プラスとマイナスの両方の数字を記載するようにしましょう。

・平方根なしで表す

なお、ルートなしで数字を表せる場合、必ず根号を外すようにしましょう。例えば、9の平方根は何でしょうか。

9の平方根を記すとき、\(\sqrt{9}\)と\(-\sqrt{9}\)は答えではありません。9は3²だからです。そのため、ルートを外さなければいけません。以下が正解です。

\(\sqrt{9}=\sqrt{3^2}=3\)
\(-\sqrt{9}=-\sqrt{3^2}=-3\)

ルートなしで表記できる場合、根号を外す必要があります。

\(\sqrt{2}\)や\(\sqrt{3}\)の値の近似値

2乗することによって、整数になる数字がルートです。しかしルートは明確な数字で表すことができません。\(\sqrt{9}\)や\(\sqrt{16}\)のように、2乗が含まれる場合は例外的に根号を外すことで、整数にすることができます。しかし、\(\sqrt{2}\)や\(\sqrt{3}\)の場合、明確な整数を記すことはできません。

ただ、近似値を記すことはできます。正確な数字ではないものの、非常に近い数字を近似値といいます。

例えば、円周率は3.1415…と無限に続きます。ただ、小学校の算数では近似値として「円周率は3.14で計算する」と習いました。これと同じように、ルートも近似値で記すことができます。例えば、以下のようになります。

\(\sqrt{2}=1.4142…\)
\(\sqrt{3}=1.7320…\)
\(\sqrt{5}=2.2360…\)

例えば、1.4の2乗は1.96です。1.5の2乗は2.25です。\(\sqrt{2}\)の近似値は1.4と1.5の間にあると分かります。これらを細かく計算していくと、\(\sqrt{2}=1.4142…\)となります。

ただ、近似値は無限に続いていきます。そのため、ルートの近似値を覚えるのは意味がありません。しかし、以下については数字を覚えておくといいです。

\(\sqrt{2}≒1.41\)
\(\sqrt{3}≒1.73\)

数学の計算では、\(\sqrt{2}\)と\(\sqrt{3}\)は頻繁に計算で出てきます。また、計算した数字が合っているのか見直しをするときに役立ちます。高校数学など、高度な数学を学ぶときであっても\(\sqrt{2}\)と\(\sqrt{3}\)の近似値は知識として非常に役立ちます。

\(\sqrt{5}\)や\(\sqrt{6}\)などの近似値を覚える意味はありません。一方で\(\sqrt{2}\)と\(\sqrt{3}\)は近似値を覚えておくと役立ちます。

有理数と無理数：整数、有限小数、循環小数は有理数

ルートを学ぶとき、同時に習う言葉に無理数があります。数学にはいくつかの分類があり、その一つが有理数と無理数です。

有理数とは、分数で表せる数のことを指します。有理数には、整数や小数があります。以下の通り、整数は分数の一つです。

\(3=\displaystyle\frac{3}{1}\)
\(5=\displaystyle\frac{5}{1}\)

小数についても、分数で表すことができます。以下のようになります。

\(0.2=\displaystyle\frac{2}{10}\)
\(1.23=\displaystyle\frac{123}{100}\)

なお無限に続いていない小数を有限小数といいます。0.2や1.23は有限小数です。小数が無限に続いているわけではなく、0.2や1.23と数字には終わりがあります。

一方で分数には、数字が無限に続いていくことがあります。例えば、以下になります。

\(\displaystyle\frac{10}{3}=3.33333…\)
\(\displaystyle\frac{13}{7}=1.85714…\)

これらの分数では、数字は無限に続いていくものの、同じ数字の繰り返しになります。例えば、\(\displaystyle\frac{13}{7}\)は1.85714285714285…のように、同じ数字が繰り返されます。このように、無限に続く規則性のある小数を循環小数といいます。

規則性のある小数は分数で表すことができます。そのため、循環小数は有理数です。つまり、以下が有理数になります。

整数
有限小数
循環小数

いずれにしても、分数で表せる数字が有理数だと理解すれば問題ありません。

円周率やルートは無理数

それに対して、数字が無限に続くものの規則性のない数字は分数で表すことができません。こうした数字を無理数といいます。無理数には円周率\((\pi)\)やルートがあります。これらの数字は以下のように規則性がありません。

\(\sqrt{2}=1.4142135…\)
\(\sqrt{3}=1.7320508…\)
\(\pi=3.14159265…\)

有理数ではない数字を無理数といいます。有理数は分数で表せるものの、それ以外の数字が無理数です。つまり、規則性がなく分数で表せない数字が無理数です。

なお、すべてのルートが無理数ではありません。例えば、\(\sqrt{4}\)は有理数です。以下のように、\(\sqrt{4}\)は2だからです。

\(\sqrt{4}=\sqrt{2^2}=2\)

中学数学では有理数と無理数の違いについて学びます。ルートは無理数の代表例であるため、平方根を学ぶときに無理数を習うのが一般的です。数学では、分数で表せない数字として無理数があることを理解しましょう。

練習問題：平方根の計算

Q1. 次の平方根を記しましょう

64
10
\(\displaystyle\frac{9}{100}\)

A1. 解答

平方根では、2乗する前の数字を指します。そこでルートを使い、答えを出しましょう。またルートを外せる場合、根号なしの数字を記すようにしましょう。答えが2つあることにも注意しましょう。

(a)

64は8²です。そのため、\(\sqrt{64}=\sqrt{8^2}=8\)です。また、\(-\sqrt{64}=-\sqrt{8^2}=-8\)です。つまり、答えは8と-8です。

(b)

答えは\(\sqrt{10}\)と\(-\sqrt{10}\)です。\(\sqrt{10}\)は無理数であり、\(\sqrt{64}\)のように整数に直すことはできません。

(c)

\(\displaystyle\frac{9}{100}\)は\(\left(\displaystyle\frac{3}{10}\right)^2\)または\(\displaystyle\frac{3^2}{10^2}\)と表すことができます。そのため、\(\displaystyle\frac{9}{100}\)の平方根は以下の2つです。