中学校の数学では確率を勉強します。確率は私たちの生活で非常に身近であり、あらゆる統計データは確率で成り立っています。
確率を学ぶからこそ、ニュースの内容が分かるようになります。また、科学での実験データは確率を用いて処理します。気象予報で雨が降るかどうかも確率です。確率の意味を理解できない場合、正しくデータを読み解くことができず、大人として日々の生活を過ごすときに支障がでます。
そのため、数学では確率を学びます。数学は日常生活で利用するために学ぶ必要があり、確率は数学の一種です。数学で確率の基礎を学ぶとき、最も頻繁に利用される例としてコインとサイコロの確率があります。
2つ以上のコインまたはサイコロを投げるとき、どのような確率になるのでしょうか。中学数学で学ぶ確率について、確率の基礎を解説していきます。
もくじ
確率とは何か?起こる確率の割合
まず、確率とは何でしょうか。確率とは、「その現象が起こる割合」を表します。例えば、サイコロを投げるとき、4の目が出る確率はいくらでしょうか。これについて、確率は\(\displaystyle\frac{1}{6}\)と誰でも答えることができます。
サイコロを投げる場合、6回サイコロを投げると、ある時点で4の目が出ると期待できます。もちろん、サイコロを投げて1回目に4の目が出るかもしれません。場合によっては、20回目でようやく4の目が出るかもしれません。ただいずれにしても、サイコロで4の目が出る確率は\(\displaystyle\frac{1}{6}\)です。
では、どのように確率を出せばいいのでしょうか。サイコロの場合、1~6まで数字があります。つまり、6通りの出方があります。6通りのうち、4の数字になるのは1つだけです。そのため、確率は\(\displaystyle\frac{1}{6}\)です。
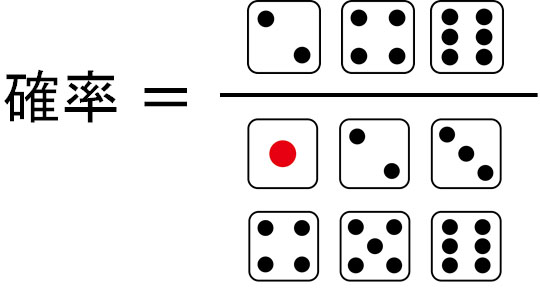
つまり確率では、以下の公式が成り立っています。

確率の計算では、その事象全体の回数を数えるようにしましょう。サイコロであれば、6通りの出方があります。それらのうち、特定の事業が起こる回数を分子に入れることで、確率を出すことができます。
例えば、サイコロで偶数が出る確率は何でしょうか。確率では偶数や奇数の問題は頻繁に出されるため、これらを理解しなければいけません。
前述の通り、サイコロは1~6通りの出方があります。この中で偶数になるのは2と4と6です。つまり、偶数になる数としては3通りがあります。そのため、サイコロで偶数が出る確率は\(\displaystyle\frac{3}{6}\)です。ただ、約分する必要があるので答えは\(\displaystyle\frac{1}{2}\)です。
奇数についても、同じやり方で確率を出せます。数学で確率の計算をするとき、「全体で何通りの方法があるのか」「その事象が起こる回数は何回か」を考えるようにしましょう。
起こる頻度が同一の「同様に確からしい」の意味
ただ確率の計算をするとき、前提条件があります。その前提条件を「同様に確からしい」といいます。同様に確からしいとは、どういう意味なのでしょうか。
サイコロを投げるとき、前述の通り4が出る確率は\(\displaystyle\frac{1}{6}\)です。それでは、以下のサイコロについても4が出る確率は\(\displaystyle\frac{1}{6}\)でしょうか。
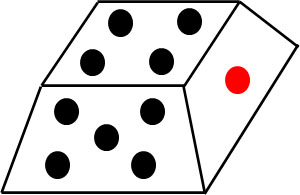
4が出る確率は\(\displaystyle\frac{1}{6}\)よりもかなり高いと予測できます。なぜ、サイコロにも関わらず、4の出る確率は\(\displaystyle\frac{1}{6}\)にならないのでしょうか。その理由としては、特定の数になりやすいようにサイコロの形状が偏っているからです。
確率の計算では、「すべての事象について発生する可能性が同じである」という前提条件が必要です。これを、同様に確からしいといいます。
例えば賭け事をするとき、多くのケースで挑戦者が負けます。この理由の一つとしては、イカサマが行われるからです。賭け事では、同様に確からしいといえるケースが少ないのです。「同様に確からしい」といえない場合、確率の計算はできません。
2枚のコインの表と裏の確率を計算する
それでは、実際に確率の計算をしてみましょう。確率の計算では、2枚のコインを投げる場面を考えます。中学数学で確率の基礎を学ぶとき、コインの例を用いて確率を学ぶことが多いです。
コインには表と裏の2種類があります。1枚のコインを投げて、表または裏が出る確率は\(\displaystyle\frac{1}{2}\)です。それでは、2枚のコインを投げる場合、どのような確率になるのでしょうか。
確率を計算するとき、直感で考えると高確率で不正解になります。そのため、確率の正しい出し方を理解しなければいけません。例えば、2枚のコインが両方とも表になる確率は何でしょうか。間違える人では、\(\displaystyle\frac{1}{3}\)と答えます。以下の種類があると考えるからです。
- 表、表
- 表、裏
- 裏、裏
そこで、より正確に考えてみましょう。例えば、以下の2つのコイン(5円、10円)があるとします。
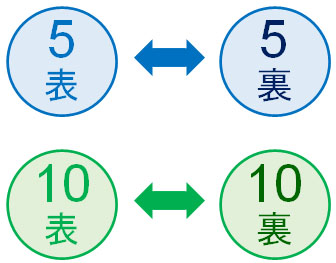
これらのコインを2つ投げると、以下の4通りが存在すると理解できます。

(表、裏)は1つだけではありません。(表、裏)と(裏、表)の2種類があります。そのため、事情が発生するトータルの数は4つです。そのため、2つのコインを投げて両方とも表になる確率は\(\displaystyle\frac{1}{4}\)です。
樹形図によって確率を求める
ただ、ヒントなしにすべての事象を書き出すのは難しいです。どのようにすれば、効率的にすべての事象を見つけることができるのでしょうか。この方法として、樹形図があります。樹形図を利用することで、すべての事象を書きだすことができます。
樹形図では、最初に1つの事象に着目します。一つのコインに着目すると、表または裏が出ます。そのため、以下のように樹形図を描くことができます。
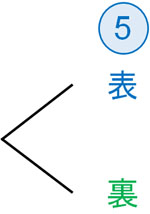
その次に、もう一方のコインを投げます。そうすると、以下のように4通りの出方があると分かります。
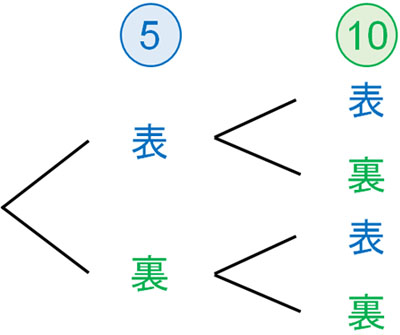
つまり、別々にコインを投げたときを仮定して、どの種類の出方があるのかすべて書き出す方法が樹形図です。同時にコインを投げても、別々にコインを投げても、コインの出方は変わりません。そこで樹形図を利用することで、すべての出方を確認するようにしましょう。
樹形図を書かないと不正解になりやすい
前述の通り、確率の計算を直感で行うと多くの人が計算ミスを犯します。つまり、樹形図を描かない場合だと、計算ミスが多発します。
なぜ、2枚のコインを投げるときに計算ミスが起こるかというと、同じ種類のコインを投げる場面を考える人が多いからです。以下のように、同じコインを2枚投げるとき、両方とも表になる確率はいくらでしょうか。

樹形図を描くとき、イベントは同時に発生するのではなく、別々に発生すると想定して描きましょう。そうすれば、すべての結果を書くことができます。
この場合、コインの種類が同じなので別の基準で樹形図を考える必要があります。そこで、「1回目のコイン」「2回目のコイン」で分けるようにしましょう。実際には2枚のコインを同時に投げるものの、樹形図を描くため、別々にコインを投げたと仮定するのです。そうすると、以下のようになります。
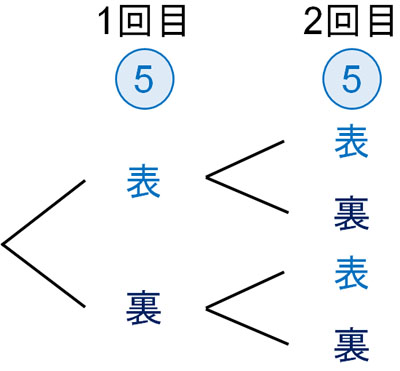
樹形図を描くとき、重要なのは「同時に起こるのではなく、別々に起こると仮定して事象を書きだす」ことです。その結果、すべての事象を書きだせるようになります。
その後、樹形図の中から「その事象が起こっている回数」を確認しましょう。例えば、2枚のコインを投げるときは以下のようになります。
- 両方とも表:1つ
- 一方が表、もう一方が裏:2つ
- 両方とも裏;1つ
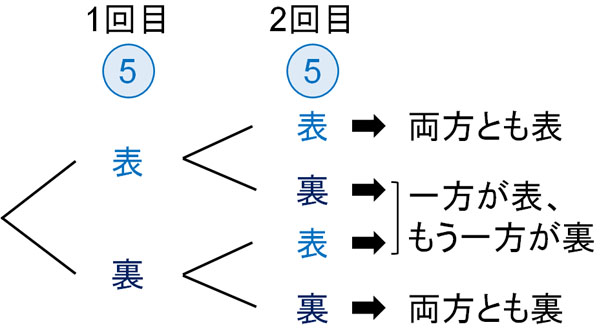
樹形図を描くことで、事情全体の回数が分かります。それと同時に、特定の事象が何回発生しているのか数えることができます。確率の基本を数学で学ぶとき、必ず樹形図を描くようにしましょう。
2つのサイコロを投げるときの確率
なおコインの確率について理解した後は、サイコロを2つ投げるときの確率について学びましょう。確率の基礎では、サイコロは頻繁に出される問題です。
2つのサイコロの大きさが同じであっても違っていたとしても、結果は同じです。コインの種類が同じであっても違っていても、確率の考え方は同じだと解説しました。樹形図を描けば、両方とも同じ答えになります。同じことはコインではなく、サイコロでもいえます。
それでは、サイコロを2つ投げる場合の樹形図はどのように考えればいいのでしょうか。まず、1回目にサイコロを投げる場合、6通りの出方があります。その後、2回目にサイコロを投げる場合、それぞれについて6通りの出方があります。
実際には同時にサイコロを投げます。ただ、これまで説明した通り、別々にサイコロを投げたと仮定して樹形図を作ります。その場合、以下のようになります。
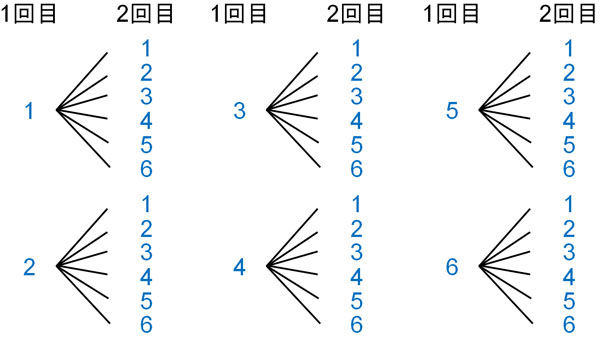
1回目のサイコロが6通りであり、2回目のサイコロは6通りです。そのため、\(6×6=36\)通りの事象が存在します。
ただ、サイコロの場合は樹形図だとこのように複雑になるため、見にくいです。また、樹形図を作るにも時間がかかります。そこでサイコロを2つ同時に投げる場合、数学では以下の表を作るのが一般的です。
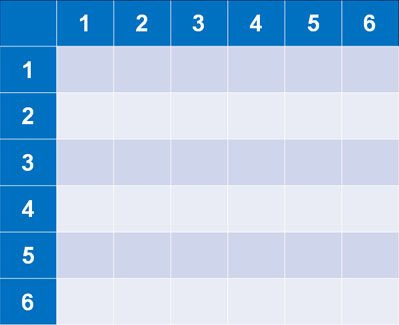
サイコロを3つ投げる場合だと利用できません。ただ、サイコロを2つ投げる場合ではこの表が有益です。
例えば、サイコロを2つ投げるとき、積が12になる確率はいくらでしょうか。この確率を出したい場合、掛け算することで12になる部分にチェックを入れましょう。以下のようになります。
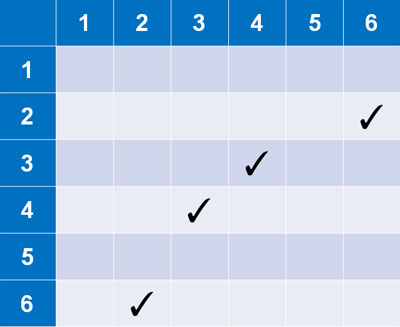
表の中では、このように積が12になるのは4通りです。全体の事象は36なので、2つのサイコロを投げて積が12になる確率は\(\displaystyle\frac{4}{36}\)です。また約分することで、答えは\(\displaystyle\frac{1}{9}\)になります。
起こらない確率を計算する
なお数学の確率では、起こらない確率を計算しなければいけないことがあります。起こる確率については、ここまで説明した方法によって計算すればいいです。一方で、起こらない確率はどのように計算すればいいのでしょうか。
起こらない確率を出すとき、考え方はこれまでの説明と同じです。まずは起こる確率を求めるようにしましょう。
例えば、20%の確率で当たるくじがあるとします。この場合、くじでハズレになる確率はいくらでしょうか。計算方法としては、以下のようになります。
- 100% – 20% = 80%
くじには、当たりとハズレの2種類しかありません。そのため、100%から当たりの確率を引くことで、ハズレになる確率(起こらない確率)が出ます。
もちろん、パーセントではなく分数でも考え方は同じです。20%は\(\displaystyle\frac{1}{5}\)と意味が同じです。つまり、当たりとなる確率は\(\displaystyle\frac{1}{5}\)です。この場合、ハズレになる確率は以下になります。
- \(1-\displaystyle\frac{1}{5}=\displaystyle\frac{4}{5}\)
「100% = 1」です。これらの事実を理解すれば、起こらない確率は以下の公式によって出せることが分かります。
- 起こらない確率\(=1-\)起こる確率
このようにして、起こらない確率を求めることができます。起こる確率だけでなく、起こらない確率の出し方も理解しましょう。
練習問題:確率の計算問題
Q1. 次の問題を解きましょう
2つのサイコロを投げます。出た数を2乗した後、2つの数を足すとき、30以下になる確率を出しましょう。
A1. 解答
サイコロの問題では、必ず表を作るようにしましょう。表を作った後、それぞれの数を2乗します。その後、足して30以下になる部分にチェックを入れましょう。以下のようになります。
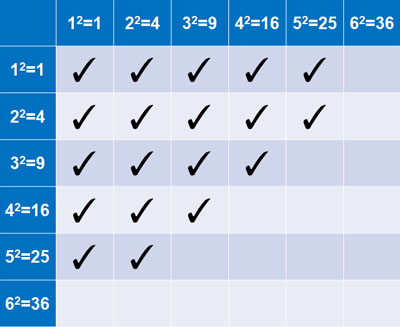
全体の事象は36です。またチェックの数は19です。そのため、以下の確率になります。
- \(\displaystyle\frac{19}{36}\)
Q2. 次の問題を解きましょう
1~3の番号が書かれた3枚の封筒があります。また、1~3の番号が書かれた3枚のカードがあります。
その後、カードをすべて封筒の中にそれぞれ入れます。封筒の番号とカードの番号がすべて違っている確率はいくらでしょうか。
A2. 解答
樹形図を描かなければ、問題を解くことはできません。そこで、樹形図を描きましょう。
もし、封筒1にカード1を入れるとどうでしょうか。この場合、封筒2にはカード2またはカード3を入れることができます。その後、封筒3には残ったカードを入れることになります。
同じように、「封筒1にカード2を入れる場合」「封筒1にカード3を入れる場合」を考えて樹形図を描いていきます。そうすると、以下のようになります。
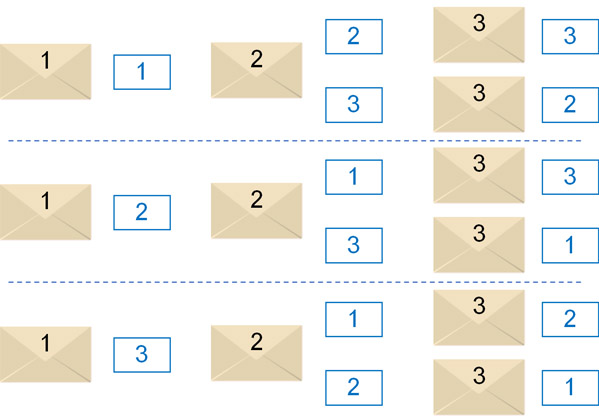
このように、全体で6通りの方法があると分かります。この中で、封筒とカードの番号がすべて違っているケースはどれでしょうか。一つずつ数えると、そうした事象は以下の2通りです。
- 封筒1(カード2)、封筒2(カード3)、封筒3(カード1)
- 封筒1(カード3)、封筒2(カード1)、封筒3(カード2)
そのため、確率は以下になります。
- \(\displaystyle\frac{2}{6}=\displaystyle\frac{1}{3}\)
確率の基礎を学び、計算を行う
数学で確率の基本を学ぶとき、最初から難解な公式を習うことはありません。樹形図を利用することで、どのようなパターンがあるのか一つずつ考えていきます。そのため、図を描かなければ答えを出すことはできません。
樹形図なしに問題を解く場合、ほぼ確実に不正解になります。コインの例で説明した通り、図を描かない場合はミスが頻発するからです。
全てのパターンを出す必要があるため、確率の問題は難易度が高いです。それだけでなく、対象の事象がどれだけ発生しているのか数えなければいけません。
これらを一つずつ行うことで、どのような確率で発生するのか分かるようになります。同時に、起こらない確率も計算できるようになります。確率を学ぶとき、これらの基本的な概念を理解しましょう。