中学数学(場合によっては小学生の算数)では、扇形(おうぎ形)の弧の長さや面積を計算しなければいけません。扇形の弧の長さと面積の求め方としては、どのように計算すればいいのでしょうか。
扇形の弧の長さや面積を計算する場合、必ず理解しなければいけないのが円の性質です。円周の長さや円の面積を計算できれば、扇形の弧の長さと面積を出すことができます。円の計算が必須なので、このときは円周率を必ず利用しなければいけません。
扇形の弧の長さや面積を出す計算問題というのは、円周や円の面積の応用問題と考えるようにしましょう。
円周や円の面積を出す公式を覚えている場合、扇形の弧の長さや面積を出すのは難しくありません。また、新たに公式を覚える必要もありません。どのようにして扇形の弧の長さと面積を出すのかについて解説していきます。
もくじ
円の直径と面積の公式では円周率を\(π\)とする
扇形の弧の長さと面積を出すためには、その前に円周と面積を必ず出さなければいけません。そのため、小学校の算数のおさらいをしましょう。
円周や面積については、以下の公式によって計算します。
- 円周 = 直径 × 3.14(円周率)
- 円の面積 = 半径 × 半径 × 3.14(円周率)
ただ中学数学では、円周率として3.14を使いません。3.14は正確な数値ではなく近似値に過ぎないからです。 その代わり、\(π\)という記号を使います。\(π\)は円周率を意味します。小学生の算数とは異なり、3.14の掛け算を省くことができるため、中学数学のほうが計算は楽です。
中学数学では、代数式として文字を使う計算をします。そこで3.14の掛け算をするのではなく、円周率を\(π\)という文字に置きかえるのです。そのため、以下の公式が成り立ちます。
- 円周 = 直径 × \(π\)
- 円の面積 = 半径 × 半径 × \(π\)
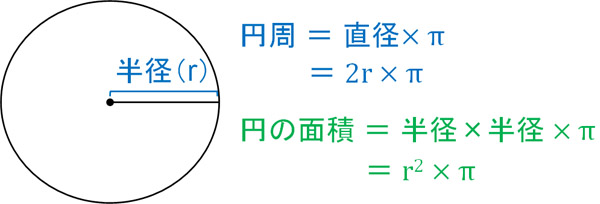
\(π\)は円周率なので、小学生の算数では\(π=3.14\)と考えて計算してもいいです。\(π\)を利用してもいいし、3.14を掛けてもいいです。どちらも正解ですが、中学数学で文字式(代数式)を習っている場合、円周率は\(π\)を使います。
円周率は定義の一つ
なお円周率について、なぜ直径に円周率を掛けると円周を出すことができるのでしょうか。それは、そのように決められているからです。
円の長さを測定した後、円の半径を測定したら、たまたま数字が約3.14だったわけです。そこで、この数字を円周率と定めました。円周率は定義の一つです。直径に円周率を掛けることで、円周になるように決められています。
そのため、「なぜ直径に円周率を掛けると円周になるのか?」と疑問に思うのは意味がありません。円周率は定義であり、たまたま約3.14という数字だったにすぎません。
同じことは、円の面積を出すときにもいえます。円周率は定義なので、円周や円の面積を出すときは公式を覚えるようにしましょう。
扇形の弧の長さと面積は中心角を使う公式がある
円の面積について、おさらいしました。なぜ、扇形の弧の長さと面積を出す前に円周や円の面積を復習することが重要になるのでしょうか。それは、円周と円の面積を理解していなければ、扇形の弧の長さと面積を出すのが不可能だからです。
扇形のうち、円周の部分を弧といいます。また、弧と2つの半径によって囲まれている角度を中心角といいます。
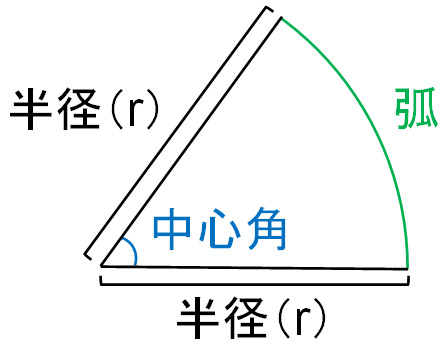
円の一部が扇形です。扇形の中で、どこが弧で中心角なのか答えられるようにしましょう。
これらの言葉を理解し、円周や円の面積の公式を学んでいる場合、扇形の弧の長さと面積を出す方法は簡単です。一応は公式があるものの、扇形の弧の長さと面積については公式を新たに覚える必要はありません。
角度(中心角)から弧の長さを計算できる
どのようにして、扇形(おうぎ形)の弧の長さを計算すればいいのでしょうか。弧の長さについては、以下の公式があります。

円周の長さを出す公式と比べると、\(\displaystyle\frac{中心角}{360°}\)が加わっています。これが、円周を出す公式です。
ただ、前述の通り覚える必要はありません。この公式については、特に覚えなかったとしても、いってしまえば当たり前の内容だからです。円の角度は全部で360°です。そのため、中心角の大きさに応じて弧の長さは変化します。
例えば、円形のケーキがあるとします。このケーキについて、2分の1に分けると中心角は180°です。また、3分の1に分けると中心角は120°です。
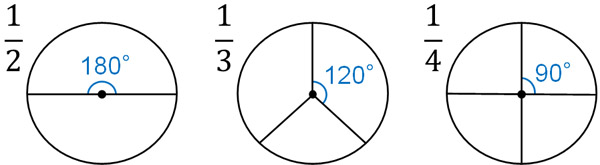
このとき、弧の長さはどうなっているでしょうか。2つに分ける場合、中心角は半分になると同時に、弧の長さも半分に減少します。3つに分ける場合、中心角は\(\displaystyle\frac{1}{3}\)になり、同時に弧の長さは\(\displaystyle\frac{1}{3}\)になります。
扇形の図形では、中心角が減少すると、同じ割合で弧の長さが減少するようになっています。そこで先に円周の長さを公式によって出し、その後に\(\displaystyle\frac{中心角}{360°}\)をかけます。そうすると、扇形の弧の長さを出すことができます。
角度から扇形の面積を求める
同じように考えると、扇形の面積を出すことができます。つまり、最初に円の面積を出します。その後、中心角の大きさに応じて扇形の面積を計算します。扇形の面積の出し方としては、以下の公式があります。

円の角度は360°です。そのため中心角が2分の1になり、180°になると、円の面積は2分の1になります。考え方は扇形の弧の長さと同じです。
同じように円の中心角が3分の1(120°)になると、面積は3分の1になります。中心角が4分の1(90°)になると、面積は4分の1になります。中心角が小さくなると、その割合に応じて扇形の面積は小さくなります。
そのため、円の面積に対して\(\displaystyle\frac{中心角}{360°}\)をかけると、扇形の面積になります。
扇形の弧の長さや面積を出す公式を覚える必要がないのは、こうした理由があるからです。円周の長さと円の面積を出す公式を覚えていれば、扇形の弧の長さと面積を出すことができます。円周や円の面積を計算した後、中心角の割合に応じて掛け算をすることで、扇形の弧の長さと面積を出しましょう。
扇形の弧の長さや面積から、中心角を計算する
これらの内容を理解すれば、扇形の中心角を計算することもできます。中心角が分からない状態であっても、扇形の弧の長さや面積が分かっている場合、中心角を出せるのです。例えば、以下の問題はどのようになるでしょうか。
- 扇形の弧の長さが\(4π\)cm、半径3cmのとき、中心角を求めましょう
扇形の弧の長さが既に分かっているケースです。この場合、中心角を\(x\)とすると以下の式を作れます。
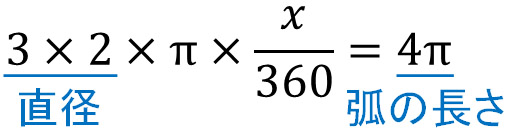
その後、この式を解きます。
\(3×2×π×\displaystyle\frac{x}{360}=4π\)
\(6π×\displaystyle\frac{x}{360}=4π\)
\(x=4π×360×\displaystyle\frac{1}{6π}\)
\(x=240\)
こうして、中心角が240°と計算できます。
練習問題:扇形(おうぎ形)の弧の長さと面積を出す
Q1. 次の問題を解きましょう
半径が6cm、弧の長さが\(2π\)の扇形について、中心角と面積を求めましょう。
A1. 解答
先に中心角を計算します。中心角を\(x\)とする場合、以下の式になります。
- \(6×2×π×\displaystyle\frac{x}{360}=2π\)
この計算をすると、以下のようになります。
\(6×2×π×\displaystyle\frac{x}{360}=2π\)
\(12π×\displaystyle\frac{x}{360}=2π\)
\(x=2π×360×\displaystyle\frac{1}{12π}\)
\(x=60\)
中心角は60°です。中心角が分かれば、円の面積を出すことができます。扇形の面積の公式に当てはめると以下のようになります。
- \(6×6×π×\displaystyle\frac{60}{360}=6π\)
そのため、扇形の面積は\(6π\)です。
Q2. 次の問題を解きましょう
以下のように、正方形の中に扇形が2つ存在します。影の面積を計算しましょう。
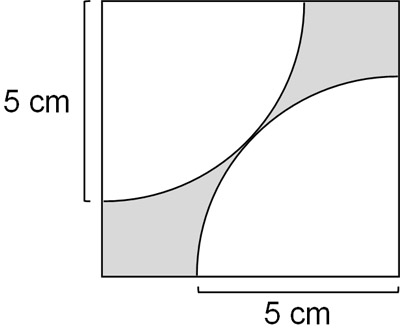
A2. 解答
扇形の応用問題では、他の図形と組み合わせて出されることがあります。この問題では、正方形と扇形との組み合わせです。影の部分の面積を出すためには、2つの図形を使う必要があります。具体的には、正方形から扇形を引けば、影の面積を出せると分かります。
- 影の面積 = 正方形の面積 – 扇形の面積
まず、扇形の面積を出しましょう。正方形の中に扇形があるため、扇形は中心角が90°です。そのため、1つの扇形は以下のように面積を計算できます。
- \(5×5×π×\displaystyle\frac{90}{360}=\displaystyle\frac{25}{4}π\)
扇形が2つ含まれているため、扇形の合計面積は以下になります。
- \(\displaystyle\frac{25}{4}π×2=\displaystyle\frac{25}{2}π\)
一方で正方形の面積はどのように出せばいいのでしょうか。以下のように考えると、斜めの線(対角線)は10cmと分かります。
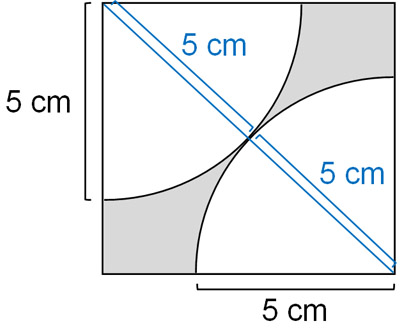
対角線が分かれば、正方形の面積を出すことができます。正方形とは、ひし形と意味が同じです。ひし形の面積は以下の公式によって出すことができます。
- 対角線 × 対角線 ÷ 2
正方形(ひし形)の場合、以下のような図形を考えることができます。
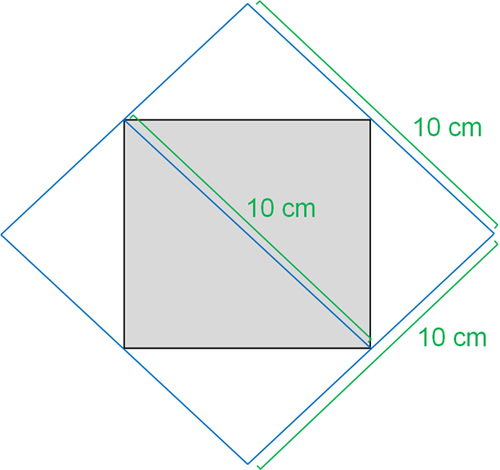
正方形の対角線が10cmなのであれば、それを囲う正方形のたてと横の長さはそれぞれ10cmになります。そのため対角線の長さを掛けることで、大きいほうの正方形の面積を出せます。ただ、出したいのはひし形(小さいほうの正方形)なので面積は半分です。
つまり、以下の計算になります。
- \(10×10×\displaystyle\frac{1}{2}=50\)
正方形の面積が50cm2であり、扇形の合計面積は\(\displaystyle\frac{25}{2}π\)cm2です。そのため、影の面積は\(50-\displaystyle\frac{25}{2}π\)cm2です。
小学生と中学生で重要な扇形の弧の長さと面積の求め方を学ぶ
数学では、小学生または中学生で扇形(おうぎ形)の図形を学びます。このとき、弧の長さと面積を計算できるようにしましょう。
円周と円の面積の公式を覚えている場合、扇形の弧の長さと面積を出す方法は簡単です。円周または円の面積を計算した後、中心角の割合に応じて数字を減らせばいいです。円の角度は360°であり、中心角が小さくなるほど、同じ割合で扇形の弧の長さや面積は小さくなります。
なお小学生の算数では、円周率を3.14で計算します。一方で中学数学では、円周率を\(π\)とします。概念は同じなので、どちらで計算してもいいです。もちろん、\(π\)の記号を使う計算のほうが3.14の掛け算を省けるため、計算ミスは少なくなります。
このようにして、扇形の弧の長さや面積を出しましょう。応用問題では他の図形と組み合わせて出題されるため、他の図形の特徴まで理解すると問題を解くことができます。