回路に存在する部品として抵抗、コイル、コンデンサーがひんぱんに利用されます。これらの部品が交流回路に存在する場合、電圧や電流、抵抗はどのように変化するのでしょうか。
交流回路に部品が一つだけ存在するときに比べて、複数の部品があると計算が大変になります。当然、式は複雑になります。交流回路に抵抗(R)、コイル(L)、コンデンサー(C)が存在する回路をRLC回路といいます。
そこでベクトル図を利用しましょう。ベクトルで考えることにより、RLC回路での抵抗(インピーダンス)を計算できるようになります。
交流回路は複雑であるものの、考え方は決まっています。そこで、どのようにRLC直列回路やRLC交流回路で回路全体の抵抗や位相のずれを計算すればいいのか解説していきます。
もくじ
インピーダンスとは何か?位相のずれの概念
抵抗(R)、コイル(L)、コンデンサー(C)が含まれている回路がRLC回路です。RLC回路で必ず出てくる単語にインピーダンスがあります。インピーダンスとは、何なのでしょうか。
インピーダンスとは、交流回路全体の抵抗を意味します。抵抗として一つの部品がある場合、抵抗の値は決まっています。またコイルやコンデンサーでは、リアクタンスとして抵抗が存在します。
ただ一つの部品ではなく、回路全体で抵抗がいくらになるのか知りたいケースは多いです。そこで、インピーダンスを利用するのです。抵抗の中でも、回路全体の抵抗を指すのがインピーダンスです。
交流回路では、時間経過と共に電圧が変化します。またそれぞれの部品は位相のずれがあるため、直流回路のように足し算によって回路全体の抵抗値を得ることができません。そこで、位相を考慮して回路全体の抵抗(インピーダンス)を計算するのです。
・RLC回路では、位相のずれを足してはいけない
つまりインピーダンスを計算するためには、位相のずれを考慮しなければいけません。例えば以下のように抵抗\(R\)、自己インダクタンス\(L\)のコイルが直列接続されている交流回路を考えてみましょう。
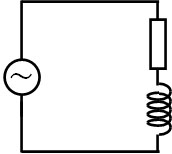
この交流回路について、位相のずれはいくらでしょうか。交流電源に対して、抵抗では位相のずれがありません。一方、コイルでは位相が\(\displaystyle\frac{π}{2}\)ずれています。そのため、多くの人は「回路全体では位相が\(\displaystyle\frac{π}{2}\)ずれている」と考えるかもしれません。
ただ、実際には違います。異なる部品が組み合わさるとき、位相のずれは\(\displaystyle\frac{π}{2}\)ではありません。そのため、どのように位相のずれを得ればいいのか理解する必要があります。
直流回路では電流を基準に位相のずれを得る
位相のずれを計算するため、基準を決めましょう。先ほどの回路は抵抗\(R\)とコイル\(L\)が直列接続しているRL回路です。そこで、この回路の位相のずれを計算しましょう。
直列回路で同じになる値に電流があります。抵抗とコイルを流れる電流\(I\)は常に同じであるため、電流を基準にすればいいとわかります。それでは、電流を基準にするときの位相のずれはどのようになるのでしょうか。
復習すると、交流回路に存在する抵抗・コンデンサー・コイルはそれぞれ以下のようになります。
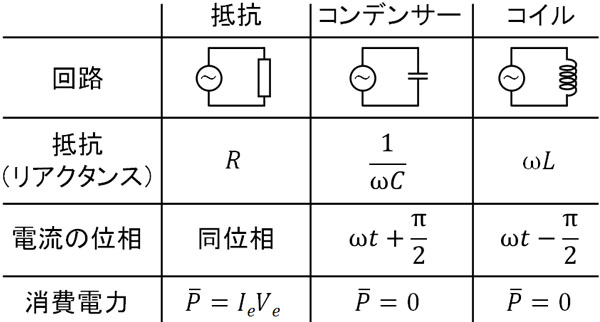
電源の電圧\(V\)を基準にするとき、コイルでの電流の位相は\(\displaystyle\frac{π}{2}\)遅れます。そのため交流電源の式が\(V=V_0sinωt\)の場合、抵抗とコイルを流れる電流の式は以下のようになります。
- 抵抗:\(I=I_0sinωt\)
- コイル:\(I=I_0sin\left(ωt-\displaystyle\frac{π}{2}\right)\)
ただ、この式は電圧を基準にするときの電流の式です。それでは、電流を基準にするときはどのように考えればいいのでしょうか。
電流を基準にするため、抵抗とコイルを流れる電流の式を\(I=I_0sinωt\)で統一しましょう。このとき、前述の通り交流電源と抵抗は同位相です。
一方、コイルの位相はずれます。このとき、電圧を基準にするときに電流の位相が\(\displaystyle\frac{π}{2}\)遅れるというのは、電流を基準にすると電圧の位相は\(\displaystyle\frac{π}{2}\)早いことを意味します。そのため、電圧の式は以下のようになります。
- 抵抗:\(V_R=RI_0sinωt\)
- コイル:\(V_L=ωLI_0sin\left(ωt+\displaystyle\frac{π}{2}\right)\)
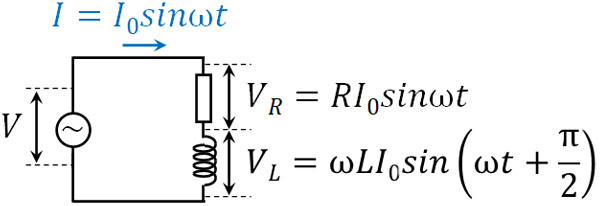
抵抗とコイルに加わる電圧は異なります。つまり、最高電圧が異なります。そこでオームの法則を利用して、抵抗の最高電圧\(V_{R0}\)を\(V_{R0}=RI_0\)としましょう。またオームの法則とリアクタンス(コイルの抵抗)を利用して、コイルの最高電圧\(V_{L0}\)を\(V_{L0}=ωLl_0\)としましょう。
それに加えて、位相のずれを考慮すると先ほどの式を作れます。電圧と電流について、どちらを基準にするのかによって位相が\(\displaystyle\frac{π}{2}\)早くなるのか、それとも遅れるのかが変わります。
各部品の電圧を足し、電源の電圧を計算する
そこで、各部品の電圧を足しましょう。後でベクトル図を解説するため、本来は以下の計算をする必要はありません。ただ、どのように足し算をするのか理解しましょう。
それぞれの電圧について、以下のように足します。
\(V=V_R+V_L\)
\(V=RI_0sinωt+ωLI_0sin\left(ωt+\displaystyle\frac{π}{2}\right)\)
加法定理を利用して、\(ωLI_0sin\left(ωt+\displaystyle\frac{π}{2}\right)\)を変形しましょう。
\(V=RI_0sinωt+ωLI_0sinωt·cos\displaystyle\frac{π}{2}\)\(+ωLI_0cosωt·sin\displaystyle\frac{π}{2}\)
\(V=RI_0sinωt+ωLI_0cosωt\)
次に、三角関数の合成を利用して計算します。
\(V=\sqrt{(RI_0)^2+(ωLI_0)^2}sin(ωt+Φ)\)
\(V=\sqrt{R^2+(ωL)^2}I_0sin(ωt+Φ)\)
三角関数の合成を利用して計算するとき、\(tanΦ=\displaystyle\frac{ωL}{R}\)を満たす角度であるとわかります。つまりこの計算結果より、角度は\(ωt+Φ\)となっているため、電圧\(V\)の位相は電流に対して\(Φ\)だけ早いとわかります。
電圧の最大値を利用し、回路のインピーダンス(抵抗)を求める
それでは、先ほどの式を利用してインピーダンスを計算しましょう。計算では、電圧の最大値を利用します。
交流電源で電圧が最大となる場合、\(sin(ωt+Φ)=1\)となります。角度がいくらになるのか不明ではあるものの、sinを利用する場合、最大値では必ず\(sinθ=1\)となります。そこで、\(sin(ωt+Φ)=1\)を代入すると以下のようになります。
- \(V_0=\sqrt{R^2+(ωL)^2}I_0\)
オームの法則\(V=RI\)を利用すると、\(\sqrt{R^2+(ωL)^2}\)は抵抗(比例定数)に該当します。比例定数の値は変わらないものの、電圧が変化することで電流が変わるのです。このとき、回路全体の抵抗(比例定数)に該当する部分をインピーダンスといいます。
インピーダンスは抵抗であるため、単位はΩです。また、記号\(Z\)を利用してインピーダンスを表すこともあります。この回路であれば、インピーダンス\(Z\)は以下のようになります。
- \(Z=\sqrt{R^2+(ωL)^2}\)
なお\(V_0=\sqrt{R^2+(ωL)^2}I_0\)に対して両辺を\(\sqrt{2}\)で割れば、実効値へ変換できます。
- \(V_e=\sqrt{R^2+(ωL)^2}I_e\)
交流回路ではインピーダンスと位相のずれが重要です。基準を設定し、位相のずれを考え、それぞれの電圧を足すことによってインピーダンスを計算しましょう。
RLC回路で利用されるベクトル図
なお実際には、前述の通り先ほどの計算をする必要はありません。数学で学ぶ三角関数の内容を利用して計算することはできるものの、RLC回路ではベクトル図を利用してインピーダンスを計算しましょう。
それでは、なぜベクトルを利用して計算することができるのでしょうか。先ほど、抵抗に加わる電圧\(V_R\)とコイルに加わる電圧\(V_L\)を足すことによって計算したため、この例を利用して確認しましょう。先ほど確認した通り、それぞれの電圧は以下のようになります。
- 抵抗:\(V_R=RI_0sinωt\)
- コイル:\(V_L=ωLI_0sin\left(ωt+\displaystyle\frac{π}{2}\right)\)
これらは円運動をしており、時間経過によって向きが異なります。ただ位相はずれているものの、円運動のスピード\(ωt\)は同じです。そのためどの時間(角度)であっても、抵抗の電圧\(V_R\)とコイルの電圧\(V_L\)は必ず90°になります。また、円運動なので最大値(長さ)に変化はありません。
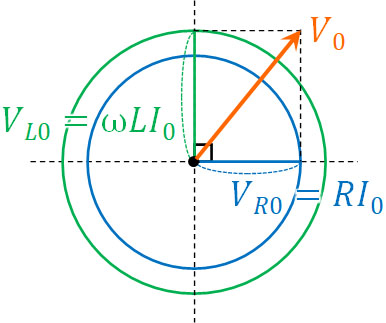
そこでわかりやすくするため、角度が0°(\(ωt=0\))の場面を考えてみましょう。図は以下のようになります。
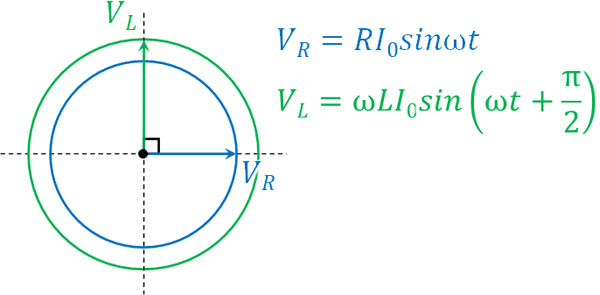
円運動について、向き(ベクトル)をもつ要素(電圧)をこの図にて示しています。そこで、ベクトルの足し算をしましょう。それぞれの電圧を足すというのは、ベクトルの足し算を意味します。このとき角度は常に90°であるため、三平方の定理を利用して計算できます。
また、それぞれの線の長さ(電圧の最高値)は抵抗が\(V_{R0}=RI_0\)、コイルが\(V_{L0}=ωLI_0\)であるため、以下のように計算できます。
\(V_0=V_{R0}+V_{L0}\)
\(V_0=\sqrt{(RI_0)^2+(ωLI_0)^2}\)
\(V_0=\sqrt{R^2+(ωL)^2}I_0\)
こうして、先ほどと同じ式を得ることができました。交流は円運動であり、ベクトルで考えることが可能であることを理解すれば、なぜベクトル図を利用して計算できるのかわかります。
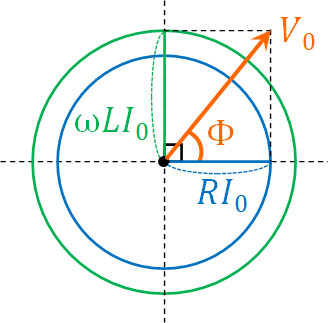
また位相のずれについては、図より以下のように計算できます。
\(tanΦ=\displaystyle\frac{V_{L0}}{V_{R0}}\)
\(tanΦ=\displaystyle\frac{ωLI_0}{RI_0}\)
\(tanΦ=\displaystyle\frac{ωL}{R}\)
交流回路の計算では、ベクトル図を使いましょう。そうすれば、三角関数の公式を利用したり、難しい計算をしたりしなくても答えを得ることができます。
RLC直列回路でそれぞれの位相のずれを得る
それでは抵抗(R)、コイル(L)、コンデンサー(C)の3つが含まれている場合はどのように計算すればいいのでしょうか。抵抗(R)、コイル(L)、コンデンサー(C)が直列接続されている交流回路をRLC直列回路といいます。
RLC直列回路について、インピーダンスを計算しましょう。直列回路であるため、それぞれの部品を流れる電流の大きさは同じです。そのため先ほどと同じように、電流を基準にしましょう。そうすると、それぞれの部品について電圧の位相のずれは以下のようになります。
- 抵抗:\(V_R=RI_0sinωt\)
- コイル:\(V_L=ωLI_0sin\left(ωt+\displaystyle\frac{π}{2}\right)\)
- コンデンサー:\(V_C=\displaystyle\frac{1}{ωC}I_0sin\left(ωt-\displaystyle\frac{π}{2}\right)\)

コンデンサーについて、電圧を基準にすると電流は\(\displaystyle\frac{π}{2}\)早くなります。そのため電流を基準にすると、電圧は\(\displaystyle\frac{π}{2}\)遅くなります。またコンデンサーのリアクタンス(抵抗)は\(\displaystyle\frac{1}{ωC}\)であるため、上記の式になります。
ベクトル図を利用してインピーダンスと位相のずれを計算する
それでは、ベクトル図を作りましょう。RLC回路では、三つのベクトルを足す必要があります。先ほどと同様に、わかりやすくするため\(sinωt=0\)の場面を考えましょう。前述の通り円運動のスピード\(ωt\)は同じなので、どの角度を基準にしても結果は同じです。
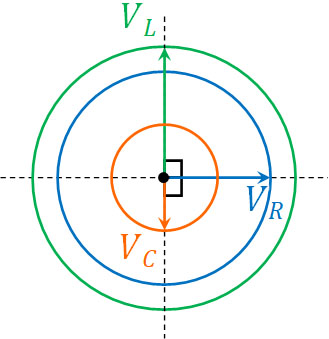
3つのベクトルを足す場合、どのように考えればいいのでしょうか。コイルの電圧\(V_L\)とコンデンサーの電圧\(V_C\)の向きは、上図のように必ず180°となります。ベクトルの向きが逆であるため、引くことができます。
また、それぞれの線の長さ(最高電圧)は以下のようになります。
- 抵抗:\(V_{R0}=RI_0\)
- コイル:\(V_{L0}=ωLI_0\)
- コンデンサー:\(V_{C0}=\displaystyle\frac{1}{ωC}I_0\)
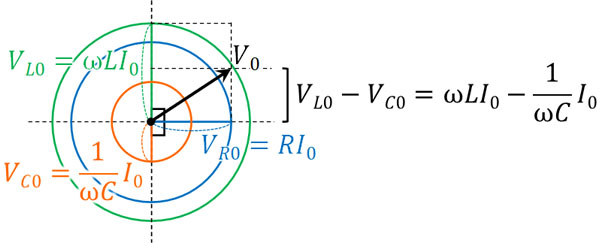
そこで三平方の定理を利用して、以下のように計算しましょう。
\(V=V_R+V_L+V_C\)
\(V_0^2=V_{R0}^2+(V_{L0}-V_{C0})^2\)
\(V_0=\sqrt{V_{R0}^2+(V_{L0}-V_{C0})^2}\)
\(V_0=\sqrt{(RI_0)^2+\left(ωLI_0-\displaystyle\frac{1}{ωC}I_0\right)^2}\)
\(V_0=\sqrt{R^2+\left(ωL-\displaystyle\frac{1}{ωC}\right)^2}I_0\)
こうして、オームの法則と同じ形を作ることができました。計算結果より、インピーダンス(抵抗)\(Z\)は以下が該当します。
- \(Z=\sqrt{R^2+\left(ωL-\displaystyle\frac{1}{ωC}\right)^2}\)
この公式を覚えても意味がないため、必ずベクトル図を利用して導き出せるようになりましょう。なお、位相のずれは図より以下のように計算できます。
\(tanΦ=\displaystyle\frac{V_{L0}-V_{C0}}{V_{R0}}\)
\(tanΦ=\displaystyle\frac{ωLI_0-\displaystyle\frac{1}{ωC}I_0}{RI_0}\)
\(tanΦ=\displaystyle\frac{ωLI_0-\displaystyle\frac{1}{ωC}}{R}\)
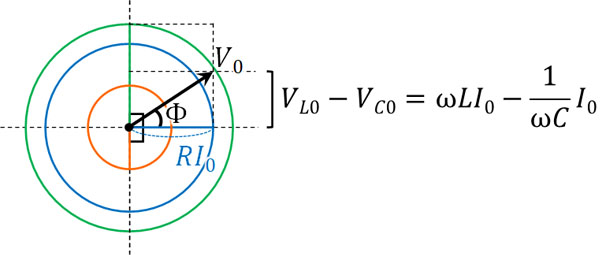
こうして、位相のずれ\(Φ\)は\(tanΦ=\displaystyle\frac{ωLI_0-\displaystyle\frac{1}{ωC}}{R}\)であるとわかりました。ベクトル図を利用することにより、RLC直列回路での位相のずれについても計算できます。
RLC並列回路では電圧を基準に位相を考える
RLC直列回路を学んだあとはRLC並列回路を理解しましょう。以下のように、交流電源に対して並列に抵抗(R)、コイル(L)、コンデンサー(C)がつながっている回路がRLC並列回路です。
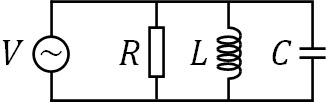
並列接続の場合、どのように考えればいいのでしょうか。途中で枝分かれしているため、それぞれの部品を流れる電流は異なります。一方、並列接続では電気的な高さが同じであるため、すべての部品で電圧が同じです。そこで、電圧を基準にしましょう。
電源の電圧が\(V=V_0sinωt\)で変化するとき、それぞれの部品を流れる電流の最高値を\(I_{R0}\)、\(I_{L0}\)、\(I_{C0}\)とすると、以下のようになります。
- 抵抗:\(I_R=I_{R0}·sinωt\)
- コイル:\(I_L=I_{L0}·sin\left(ωt-\displaystyle\frac{π}{2}\right)\)
- コンデンサー:\(I_C=I_{C0}·sin\left(ωt+\displaystyle\frac{π}{2}\right)\)
電圧を基準にするとき、電流の位相のずれは既に学んでいるため、問題なく理解できると思います。次に、オームの法則とリアクタンスを用いて先ほどの式を以下のように変形しましょう。
- 抵抗:\(I_R=\displaystyle\frac{V_0}{R}sinωt\)
- コイル:\(I_L=\displaystyle\frac{V_0}{ωL}sin\left(ωt-\displaystyle\frac{π}{2}\right)\)
- コンデンサー:\(I_C=ωCV_0sin\left(ωt+\displaystyle\frac{π}{2}\right)\)
こうして、それぞれの部品を流れる電流の式がわかります。
ベクトル図を利用し、インピーダンスと位相差を得る
それでは、先ほど計算した式を利用して電流の合計を計算しましょう。つまり、以下の足し算をします。
- \(I=I_R+I_L+I_C\)
そこで、ベクトル図を作りましょう。それぞれ円運動をしており、位相はずれているものの、角度が変化するときのスピード\(ωt\)は同じです。これらの性質を利用して、以下の図を描くのです。
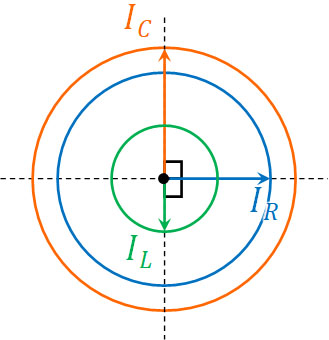
わかりやすくするため、先ほどと同じように、\(sinωt=0\)のときを利用して以下のようにベクトル図を作りましょう。
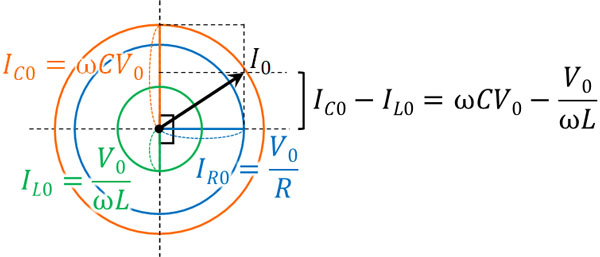
このように長さを計算し、ベクトルの足し算をすると、以下のように計算できます。
\(I=I_R+I_L+I_C\)
\(I_0^2=I_{R0}^2+(I_{C0}-I_{L0})^2\)
\(I_0=\sqrt{I_{R0}^2+(I_{C0}-I_{L0})^2}\)
\(I_0=\sqrt{\left(\displaystyle\frac{V_0}{R}\right)^2+\left(ωCV_0-\displaystyle\frac{V_0}{ωL}\right)^2}\)
\(I_0=\sqrt{\displaystyle\frac{1}{R^2}+\left(ωC-\displaystyle\frac{1}{ωL}\right)^2}V_0\)
\(V_0=\displaystyle\frac{1}{\sqrt{\displaystyle\frac{1}{R^2}+\left(ωC-\displaystyle\frac{1}{ωL}\right)^2}}I_0\)
こうして、オームの法則\(V=RI\)と同じ形にすることができました。つまり、回路全体のインピーダンス(抵抗)\(Z\)は以下になります。
- \(Z=\displaystyle\frac{1}{\sqrt{\displaystyle\frac{1}{R^2}+\left(ωC-\displaystyle\frac{1}{ωL}\right)^2}}\)
また、ベクトル図を利用することでRLC並列回路の位相差を計算しましょう。
\(tanΦ=\displaystyle\frac{I_{C0}-I_{L0}}{I_{R0}}\)
\(tanΦ=\displaystyle\frac{ωCV_0-\displaystyle\frac{V_0}{ωL}}{\displaystyle\frac{V_0}{R}}\)
\(tanΦ=R\left(ωC-\displaystyle\frac{1}{ωL}\right)\)
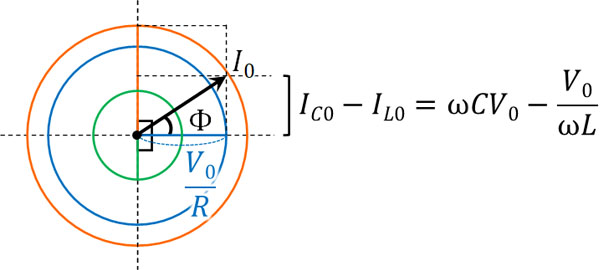
こうして、ベクトル図を利用することで位相のずれを計算することができました。
RLC回路で位相のずれを確認し、インピーダンスを計算する
交流回路に抵抗、コイル、コンデンサーが存在するケースがあります。そこで複数の部品が回路内に存在するとき、各部品で起こる位相のずれを計算できるようになりましょう。
このとき重要になるのがベクトル図です。交流電源では、円運動を利用して計算します。そこでベクトルの足し算を利用することで、電圧または電流の式を得ることができます。
また計算した式を利用して、電圧または電流の最高値を得る式を作りましょう。これにより、オームの法則と比較することで、インピーダンスを得ることができます。回路全体の抵抗がインピーダンスです。またベクトル図を利用して位相のずれも計算できます。
RLC直流回路でもRLC並列回路でも、ベクトル図を利用することによってインピーダンスと位相のずれを計算できます。そこでベクトル図の概念を学び、どのように計算すればいいのか方法を理解しましょう。






