熱を加えることによって温度が高くなります。また、物質によって温まりやすかったり、温まりにくかったりと違いがあります。物理では、この違いを数式によって表します。
熱力学で利用される温度は絶対温度です。セルシウス温度(℃)ではなく、絶対温度(K)を利用して計算しましょう。
物質の温度変化は熱容量や比熱を利用して計算できます。また、私たちは熱が移動することを知っています。熱の移動では熱量保存の法則を適用することができ、どれだけ熱が移動したのか計算できます。これにより、物質を状態変化させるために必要な熱量の計算も可能です。
私たちにとって熱は身近です。そこで、物理で学ぶ熱の概念や熱容量・比熱の計算方法を解説していきます。
もくじ
熱運動の激しさを表すのが温度
まず、温度とは何でしょうか。私たちが熱い、または冷たいなどの感覚を得るとき、熱が関与しています。
分子は目に見えません。そこで、仮に分子が目に見えるとしましょう。この場合、温度が高いと水分子や酸素分子、窒素分子などは積極的に空気中を動きます。一方で温度が低い場合、分子の動きは弱くなります。
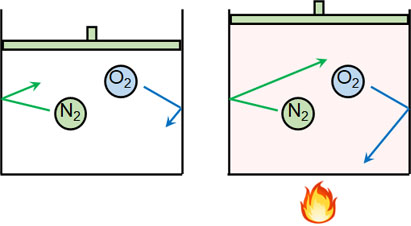
つまり温度というのは、熱運動の激しさを表すのです。水分子であれば、温度が高いと空気中を激しく動き回ります。一方で温度が低いと水となり、熱運動の激しさは弱くなります。より温度が低いと氷となって固まり、その場で弱く振動することになります。
熱を加えると温度が上昇します。このとき温度が上がるというのは、「分子がどれだけ激しく動くのか」を表していると理解しましょう。
セルシウス温度(℃)と絶対温度(K)
このとき利用する温度に絶対温度(K)があります。ほとんどの国では、セルシウス温度(℃)を利用することによって温度を表します(アメリカでは華氏を利用する)。
ただ物理や化学で温度を利用するとき、セルシウス温度を利用しません。セルシウス温度は氷が溶ける温度(0℃)を基準にしています。ただ世の中に存在する物質は水だけではなく、非常に多くの物質が存在します。そこで、絶対温度(K)を利用しましょう。
これ以上、下げることのできない温度を絶対零度といいます。つまり、絶対零度よりも低い温度は存在しません。絶対零度はセルシウス温度で-273℃です。
そこで物理や化学で熱量を計算するとき、セルシウス温度に対して273を足しましょう。これにより、絶対温度を得ることができます。例えば27℃は300Kです。絶対零度を基準にして計算することにより、すべての物質に対して法則や公式を適用できるようになります。
熱容量と温度変化の関係
絶対温度の概念を学ぶことにより、ようやく熱容量を理解できるようになります。熱容量は以下のように定義されています。
- 物体の温度を1K上げるために必要な熱量
1K上げるというのは、要は温度を1℃上げるために必要な熱量を意味します。空気や水、鉄などに熱を加えると、温度が上昇します。ただどのような物体に熱を加えるのかによって、温度を1K(1℃)上昇させるために必要な熱量が異なります。そこで、熱容量を利用します。
なお、熱量の単位はJ(ジュール)です。そのため熱容量\(C\)の単位はJ/Kになります。例えば熱容量10J/Kの物体Aでは、温度を5K上げるために50Jの熱量が必要です。一方で熱容量20J/Kの物体Bでは、温度を5K上げるために100Jの熱量が必要です。
物体Aと物体Bを比較すると、温度を5K上昇させるために必要な熱量は物体Bのほうが大きいです。つまり、物体Bのほうが温まりにくいことを意味します。
物体の種類によって比熱が異なる
それでは物体の温まりやすさではなく、物体の種類による温まりやすさはどのように表せばいいのでしょうか。
当然ながら、質量が重い物体であるほど温まりにくいです。温まりやすい材質であっても、質量が大きいと全体では温まりにくくなるのです。言い換えると、質量が大きいと熱容量が大きくなります。
例えば、水に比べて鉄などの金属は熱伝導性が優れており、温まりやすいことで知られています。ただ鉄の塊100kgと水1gでは、当然ながら水1gのほうが温まりやすいです。そのため物体の種類に着目して温まりやすさを比較したい場合、質量を同じにして比べなければいけません。
そこで、比熱を利用しましょう。比熱の定義は以下になります。
- 1gの物体の温度を1K上げるために必要な熱量
比熱\(c\)の単位はJ/(g·K)です。1gを基準にして、必要な熱量を計算するときは比熱を利用しましょう。
なお比熱\(c\)の単位を確認してわかる通り、物体の質量\(m\)と温度変化\(ΔT\)をかけることにより、必要な熱量\(Q\)を得ることができます。そのため、以下のように表すことができます。
- \(Q=mcΔT\)
この公式を覚える必要はありません。比熱の定義を理解し、単位を確認すれば、比熱に質量と温度変化をかけることで熱量\(Q\)を得られるとわかります。
例えば水の比熱は4.2J/(g·K)と知られています。それでは、20gの水を5K上昇させるために必要な熱量はいくらでしょうか。以下のように計算しましょう。
- \(4.2×20×5=420\)
こうして、答えは420Jであるとわかります。
質量と比熱をかけると熱容量になる
なお前述の通り、質量を考慮しない場合は熱容量\(C\)となります。比熱の単位はJ/(g·K)である一方、熱容量の単位はJ/Kです。そのため比熱\(c\)に対して、物体の質量\(m\)をかけると熱容量\(C\)となります。
- \(C=mc\)
そこで熱容量\(C\)と温度変化\(ΔT\)を利用することにより、熱量\(Q\)を以下のように表すことができます。
- \(Q=CΔT\)
比熱と同様に、この公式を覚える必要はありません。熱容量の定義と単位を学べば、熱容量に温度変化をかけることで熱量を得られるのは明確だからです。ひとまず、比熱と熱容量の関係を理解しましょう。
熱平衡による熱の移動:熱量保存の法則
熱を加えることにより、物質の温度が上昇することは既に理解していると思います。つまり、熱は移動します。熱い物体と冷たい物体をくっつけると、熱が移動し、最終的に同じ温度になることは容易に想像できます。熱湯に氷を入れると、熱湯の温度は低くなり、氷は溶けて水になるのです。
熱い物体と冷たい物体をくっつけると、等しい温度になる現象を熱平衡といいます。
熱平衡となるとき、高温の物体Aと低温の物体Bについて、物体Aが失った熱量\(Q_A\)と物体Bが得た熱量\(Q_B\)は同じになります。これを熱量保存の法則といいます。
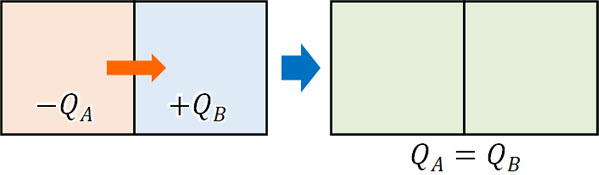
熱平衡による熱量保存の法則を利用すれば、熱量や熱容量、比熱、温度変化の計算が可能になります。例えば、以下の答えは何でしょうか。
- 質量100gの金属製の容器に水50gを加え、温度を測ると20℃でした。この容器に40℃のお湯を30g加えると、全体の温度は25℃になりました。水の比熱は4.2J/(g·K)であり、熱の出入りはありません。金属の比熱はいくらですか。
熱量保存の法則を利用するため、熱量に着目しましょう。お湯に着目すると、40℃から25℃に減っているため、15Kの温度が下がっています。そのため、30gのお湯が失った熱量\(Q\)は以下になります。
\(Q=4.2×30×15=1890\)
つまり、お湯は1890Jの熱量を失っているとわかります。そのため熱量保存の法則より、もう一方は1890Jの熱を得ているとわかります。
金属容器と水は20℃から25℃に温度が上昇しています。つまり、温度は5K上がっています。そのため金属容器の比熱を\(c\)とすると、以下の式を作れます。
\(1890=100c×5+4.2×50×5\)
\(500c=1890-1050\)
\(500c=840\)
\(c=1.68\)
こうして、金属の比熱は1.68J/(g·K)とわかります。なお有効数字2ケタであれば、金属の比熱は1.7J/(g·K)です。
水の状態変化と時間の関係
なお同じ物質であっても、状態によって温度変化が異なります。例えば水の比熱は4.2J/(g·K)であるものの、氷の比熱は2.1J/(g·K)です。固体と液体では比熱が違うため、分けて考えなければいけません。
また物体が状態変化するとき、分子の結合を切る必要があるなど、エネルギーが必要になります。そのため、例えば水であれば、熱を加えても温度が上がらない状態があります。以下のように、固体から液体、または液体から気体へ変化するときは熱を加えても温度が一定です。
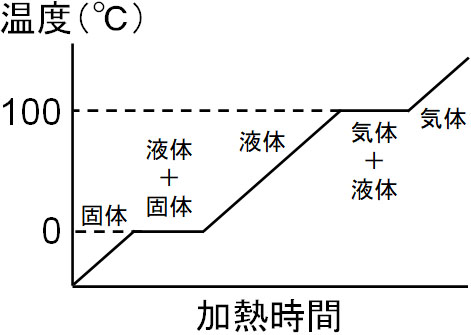
水と氷が混ざっている状態では、温度は0℃です。液体(水)と気体(水蒸気)が混ざっている場合、温度は100℃です。このとき物質の融解に必要な熱を融解熱、蒸発に必要な熱を蒸発熱といいます。
物質の状態によって比熱が違いますし、状態変化するときに必要な熱量も異なります。そのため状態変化を伴う場合、これらを考慮して計算しましょう。例えば、以下の問題の答えは何でしょうか。
- -10℃の氷100gを30℃にするために必要な熱量はいくらでしょうか。なお氷の比熱は2.1J/(g·K)、水の比熱は4.2J/(g·K)であり、氷の融解熱は340J/gです。
氷から水になるため10℃上昇し、そのあとに30℃上昇しています。また氷が水になるために必要な融解熱を加えましょう。そのため、式は以下のようになります。
\(2.1×100×10+340×100\)\(+4.2×100×30\)
\(=48700\)
こうして、答えは48700Jとわかります。
熱容量、比熱、熱量保存の法則を利用して計算する
物理で熱力学を学ぶとき、最も基本的な内容が熱と温度です。温度とは何かを学び、熱と温度の関係性を理解しましょう。
物理で温度を計算するとき、セルシウス温度だけでなく、絶対温度を知っておく必要があります。絶対零度を基準とするため、絶対温度に変えるためにはセルシウス温度に273を足しましょう。
温度の概念を理解したら、熱容量や比熱を学ぶことになります。温度を上昇させるために必要な熱量を計算するとき、熱容量と比熱を利用します。また熱平衡では熱量保存の法則が成り立つため、熱が移動するときの変化を計算できるようになりましょう。
熱力学では、熱量を計算できるようになるのは必須です。熱量の計算は難しくないため、熱容量と比熱の定義を学び、熱量保存の法則を利用できるようになりましょう。






