多くの分子が壁に衝突することによって圧力が生まれます。そのため一つの分子に着目することによって、圧力を計算することができます。
それでは、一つの分子を利用して圧力を計算するためには、どのようにすればいいのでしょうか。気体の分子運動を計算する過程は複雑です。そのため解き方を知っていれば問題を解けるものの、解き方を知らなければ問題を解けません。
物理を学ぶとき、公式を暗記しても意味がありません。そこで、公式の導出方法を理解しましょう。そうすれば、気体の分子運動と圧力の関係がわかります。
気体が移動するときのルールを学び、一つの分子の運動から圧力を計算しましょう。そこで、どのように気体の分子運動を計算すればいいのか解説していきます。
もくじ
気体分子が移動するときのルール
まず、気体分子が移動するときのルールを知りましょう。ルールがわかっていない場合、気体の分子運動を計算することはできません。
物理では前提条件が重要です。例えば、実際には理想気体は存在しません。ただ気体を理想気体であると仮定することにより、気体の状態方程式を利用できるのです。同じように、気体分子が移動するときも前提条件を設定します。以下のルールを作りましょう。
- 分子は一定の速さにて、直線で進む(等速直線運動)
- 分子が壁と衝突しても速さは変わらない
- 理想気体であり、重力を無視できる
分子は理想気体であるため、分子に大きさが存在せず、分子同士が衝突することはありません。またほかの分子による影響を受けないため、慣性の法則によって常に同じスピードで動いています。
このルールがなければ、気体の分子運動と圧力の関係を得ることができません。なお計算をするとき、一つの分子に着目して気体の運動を計算し、最終的に圧力を得ることになります。
一つの分子を利用し、圧力を計算する
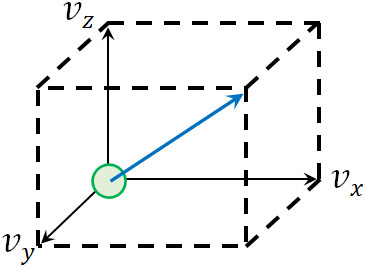
立方体の中に存在する分子について、気体の分子運動を計算しましょう。立体であるため\(x\)軸、\(y\)軸、\(z\)軸が存在します。また、一つの辺の長さを\(L\)とします。
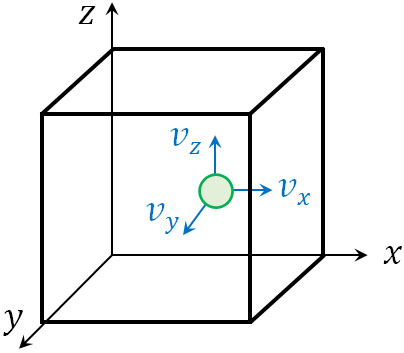
分子は空間を移動しているものの、物理では特定の方向のみ考えて計算すればいいです。例えば\(x\)軸に着目する場合、\(x\)軸方向の成分に分解しましょう。
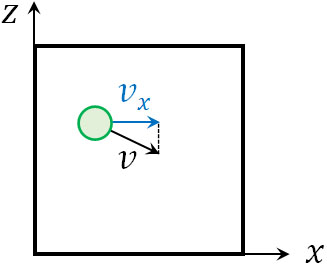
一つの成分に着目すればいいと理解すると、計算が容易になります。
一つの分子の力積を求める
それでは、一つの分子について力積を求めましょう。一つの分子の質量が\(m\)であり、\(x\)軸方向に速度\(v_x\)で進んでいる場合、運動量は\(mv_x\)です。
また前述の通り、分子が壁に衝突してはね返った後の速さは同じであり、常に同じ速さで進みます。はね返った後の分子の速度は\(-v_x\)となるため、運動量は\(-mv_x\)へと変化します。そのため、力積を以下のように表せます。
\(-mv_x-(mv_x)=-2mv_x\)

つまり、一つの分子が受ける力積は\(-2mv_x\)です。
それでは、一つの分子によって壁が受ける力積はいくらでしょうか。作用・反作用の法則により、壁が受ける力積は分子が受ける力積と等しくなります。そのため、壁が受ける力積は\(2mv_x\)です。
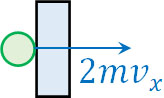
分子が受ける力積は\(-2mv_x\)であるため、壁が受ける力積は符号が逆になります。
気体分子が再び同じ壁に衝突するまでの時間
分子が壁に衝突した後、分子は他の壁に衝突することによってはね返り、再び同じ壁と衝突します。分子は同じ壁と何度も衝突するのです。
そこで気体分子が衝突した後、再び同じ壁に衝突するまでの時間を計算しましょう。\(x\)軸上の壁に衝突した後、\(x\)軸方向に距離\(2L\)を移動すると、再び同じ壁に衝突します。
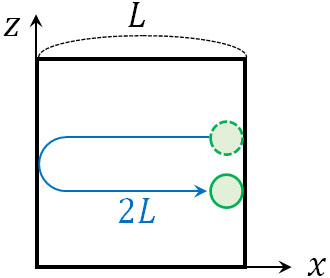
速さは\(v_x\)であるため、再び同じ壁に衝突するまでにかかる時間\(t\)と移動距離\(2L\)を利用すると、以下の式を作ることができます。
\(v_xt=2L\)
\(t=\displaystyle\frac{2L}{v_x}\)
同じ速度で分子が移動する場合、再び同じ壁に衝突するまでにかかる時間は\(\displaystyle\frac{2L}{v_x}\)とわかりました。
分子が1秒間に壁へ衝突する回数
次に、分子が1秒間に壁へ衝突する回数を計算しましょう。前述の通り、\(t=\displaystyle\frac{2L}{v_x}\)秒間で1回、壁に衝突します。それは、1秒間では何回壁に衝突するでしょうか。分子が1秒間に壁へ衝突する回数を\(n\)とすると以下の比例関係を作れます。

この式を解きましょう。
\(\displaystyle\frac{2Ln}{v_x}=1\)
\(n=\displaystyle\frac{v_x}{2L}\)
計算により、1秒間で一つの分子は\(\displaystyle\frac{v_x}{2L}\)回、壁に衝突するとわかりました。
すべての気体分子が1秒間で壁へ与える力
それでは、1秒間で一つの分子が壁に与える力積はいくらでしょうか。先ほど計算した通り、一つの分子が壁に一回衝突する場合、力積は\(2mv_x\)です。
ただ分子は1秒間に1回ではなく、1秒間に\(\displaystyle\frac{v_x}{2L}\)回壁に衝突します。そのため、一つの分子が1秒間で壁に与える力積の合計は以下になります。
\(2mv_x×\displaystyle\frac{v_x}{2L}=\displaystyle\frac{mv_x^2}{L}\)
なお力積は\(FΔt\)で計算できます。1秒での力積を計算しているため、\(Δt=1\)秒です。そのため、以下のようになります。
\(F×1=\displaystyle\frac{mv_x^2}{L}\)
\(F=\displaystyle\frac{mv_x^2}{L}\)
つまり、一つの分子が1秒間で壁に与える力\(F\)は\(\displaystyle\frac{mv_x^2}{L}\)となります。
すべての分子が壁へ与える力を得る
次に、すべての分子が壁へ与える力を計算しましょう。計算方法は簡単であり、立方体の中に存在する分子の数\(N\)をかけましょう。例えばすべての分子が速さ\(v_x\)で移動している場合、すべての分子が壁へ与える力は\(\displaystyle\frac{Nmv_x^2}{L}\)です。
ただ、一つ問題点があります。すべての分子が同じ速さで移動していることはありません。分子によってスピードは異なります。そこで\(v_x^2\)の代わりとして、\(x\)軸方向の速さの二乗の平均値である\(\overline{v_x^2}\)(すべての分子の速さの二乗の平均値)を利用しましょう。そうすると、以下の式を得ることができます。
- \(F=\displaystyle\frac{Nm\overline{v_x^2}}{L}\)
こうして、立方体に存在するすべての分子が壁へ与える力\(F\)を計算することができました。
分子による圧力の計算を行う
\(F=\displaystyle\frac{Nm\overline{v_x^2}}{L}\)とわかったため、圧力の計算が可能です。立方体の一辺の長さは\(L\)であるため、\(x\)軸の壁の面積は\(L^2\)です。そこで、\(F=\displaystyle\frac{Nm\overline{v_x^2}}{L}\)を面積\(L^2\)で割ることで圧力\(P\)を出しましょう。
\(P=\displaystyle\frac{Nm\overline{v_x^2}}{L}÷L^2\)
\(P=\displaystyle\frac{Nm\overline{v_x^2}}{L^3}\)

なお\(L^3\)というのは、立方体の体積\(V\)を意味します。そのため、以下のように圧力\(P\)を変形できます。
- \(P=\displaystyle\frac{Nm\overline{v_x^2}}{V}\)
こうして、体積\(V\)を利用して\(x\)軸方向の圧力\(P\)を得ることができます。
・圧力を計算する
ただ、ここまでした計算は\(x\)軸方向のみについて、分子が1秒間に壁へ与える力です。それでは\(x\)軸、\(y\)軸、\(z\)軸のすべてを考慮する場合、圧力はどのようになるのでしょうか。
立方体の辺の長さはすべて同じであるため、当然ながら\(y\)軸と\(z\)軸についても先ほどと同じ答えを得ることができます。そのため、以下のようになります。
- \(y\)軸:\(P=\displaystyle\frac{Nm\overline{v_y^2}}{V}\)
- \(z\)軸:\(P=\displaystyle\frac{Nm\overline{v_z^2}}{V}\)
そこで\(x\)軸の圧力だけでなく、\(y\)軸と\(z\)軸に加わる圧力を足すと以下のようになります。
\(3P=\displaystyle\frac{Nm\overline{v_x^2}}{V}+\displaystyle\frac{Nm\overline{v_y^2}}{V}+\displaystyle\frac{Nm\overline{v_z^2}}{V}\)
\(P=\displaystyle\frac{Nm}{3V}(\overline{v_x^2}+\overline{v_y^2}+\overline{v_z^2})\)
なお三平方の定理より、\(\overline{v_x^2}\)、\(\overline{v_y^2}\)、\(\overline{v_z^2}\)、\(\overline{v^2}\)には以下の関係があります。
- \(\overline{v_x^2}+\overline{v_y^2}+\overline{v_z^2}=\overline{v^2}\)
そこで、式を以下のように変えましょう。
- \(P=\displaystyle\frac{Nm\overline{v^2}}{3V}\)
こうして、一つの分子による力を利用することにより、圧力\(P\)が\(\displaystyle\frac{Nm\overline{v^2}}{3V}\)になると計算できました。
公式として\(P=\displaystyle\frac{Nm\overline{v^2}}{3V}\)を覚えても意味がありません。必ず公式の出し方を学びましょう。そうすれば、応用問題が出されても問題を解けるようになります。
理想気体の状態方程式と公式の比較を行う:ボルツマン定数
圧力を計算することができたら、次に理想気体の状態方程式と比較しましょう。前述の通り、気体分子が理想気体であることを前提に公式を導出しています。そのため\(P=\displaystyle\frac{Nm\overline{v^2}}{3V}\)が成り立つ場合、気体の状態方程式も成り立ちます。
そこで、\(P=\displaystyle\frac{Nm\overline{v^2}}{3V}\)の両辺に\(V\)をかけましょう。以下のようになります。
- \(PV=\displaystyle\frac{Nm\overline{v^2}}{3}\)
気体の状態方程式より、\(PV=nRT\)です。そのため\(PV\)を消去すると、以下の式を作れます。
- \(\displaystyle\frac{Nm\overline{v^2}}{3}=nRT\)
なお\(N\)は立方体に存在する分子数であるため、物質量\(n\)とアボガドロ数\(N_A\)を利用し、\(n=\displaystyle\frac{N}{N_A}\)と表すことができます。化学の知識にはなりますが、物質量とアボガドロ数の定義を利用して式を作る必要があります。
\(n=\displaystyle\frac{N}{N_A}\)であるため、先ほどの式を以下のように変形できます。
\(\displaystyle\frac{Nm\overline{v^2}}{3}=\displaystyle\frac{N}{N_A}RT\)
\(\displaystyle\frac{m\overline{v^2}}{3}=\displaystyle\frac{RT}{N_A}\)
なおアボガドロ数\(N_A\)は一定であり、気体定数\(R\)も一定です。そのため\(\displaystyle\frac{R}{N_A}\)は定数であり、値が変わることはありません。そこで、\(\displaystyle\frac{R}{N_A}=k\)としましょう。
- \(\displaystyle\frac{m\overline{v^2}}{3}=kT\)
なお、\(\displaystyle\frac{R}{N_A}=k\)をボルツマン定数といいます。大学の統計力学では、ボルツマン定数を利用することになります。
なお式を確認すると、分子の速さ\(v\)は温度\(T\)によって決まることがわかります。熱力学では、温度は分子運動の激しさを表します。つまりスピードの速い分子がたくさんあると、その分だけ温度も高くなるのです。この理由は、式を確認することでわかります。
分子一つの平均運動エネルギー:温度で分子のエネルギーが決まる
次に分子の運動エネルギーに着目しましょう。運動エネルギーは\(\displaystyle\frac{1}{2}mv^2\)で得ることができます。そこで先ほどの式を変形し、\(\displaystyle\frac{1}{2}mv^2\)の形にしましょう。
\(\displaystyle\frac{m\overline{v^2}}{3}=kT\)
\(\displaystyle\frac{1}{2}m\overline{v^2}=\displaystyle\frac{3}{2}kT\)
こうして、分子一つの運動量は\(\displaystyle\frac{3}{2}kT\)になると計算できました。
式を確認すると、温度\(T\)が決まれば、分子の運動量も決定することがわかります。気体の種類に関係なく、温度が運動量の決定要因なのです。また運動量は圧力\(P\)や体積\(V\)に影響されず、温度\(T\)のみに依存するとわかります。
数式を得ることによって、物質の性質を理解できます。ここまでの内容を理解すれば、なぜ分子の速さが温度と関係しているのかわかります。
計算によって気体の分子運動と圧力、温度の関係を学ぶ
計算方法を知っていれば解けるものの、計算の過程を知らなければ気体の分子運動に関する問題を解くことはできません。そこで、どのように分子による力の影響を計算すればいいのか理解しましょう。
気体の分子運動を計算するとき、一つの分子に着目します。これによって\(x\)軸方向での力や圧力の計算が可能です。
また計算により、立方体に存在する分子全体の圧力を計算できます。これにより、分子の速さ(運動エネルギー)と温度の関係がわかります。また、分子の速さに圧力や体積は影響しないこともわかります。
数式を計算することにより、自然現象の仕組みがわかります。分子による力積を計算し、圧力や温度の関係を把握できるようになりましょう。






