物理や化学で気体を取り扱うとき、必ず利用するのが気体の状態方程式です。気体の状態方程式を利用するとき、重要な法則にボイル・シャルルの法則があります。
ボイル・シャルルの法則では、ボイルの法則とシャルルの法則を組み合わせることになります。気体の状態方程式では、質量数が一定なのであれば、圧力や体積、温度の関係は常に同じになります。この性質がボイル・シャルルの法則です。
物理や化学の中でも、ボイル・シャルルの法則は理解しやすいです。気体の状態方程式を覚えている場合、問題なく計算問題を解くことができます。
それでは、ボイル・シャルルの法則とは何でしょうか。どのようにボイル・シャルルの法則を利用して計算問題を解けばいいのか解説していきます。
もくじ
分子の衝突によって圧力を生じている
ボイル・シャルルの法則を理解するとき、まずは世の中の自然現象に着目しましょう。例えば、体積を変化させることのできる密封容器に気体の分子を入れます。この容器について、熱を加えればどうでしょうか。
熱によって分子の動きは激しくなります。そのため、密封容器の体積は大きくなります。
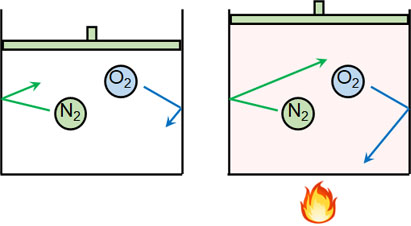
通常、気体は目に見えません。そのため想像しにくいですが、圧力は分子による壁への衝突によって起こっています。熱を加えると圧力が高くなったり、容器の体積が増えたりするのは、分子による衝突の度合いが大きくなるからなのです。
ボイルの法則:圧力と体積のかけ算は常に一定
それでは、ボイルの法則から確認していきましょう。ボイルの法則とは、物質量と温度が一定の場合、圧力と体積のかけ算は等しいことを表します。
気体の状態方程式は以下のように表されます。
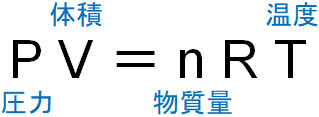
物質量と温度が同じであれば、圧力と体積のかけ算が常に一定になるのは容易にわかります。そのため圧力を2倍にしたら、体積は\(\displaystyle\frac{1}{2}\)になります。また圧力を\(\displaystyle\frac{1}{3}\)にしたら、体積は3倍になります。
そのため、ボイルの法則では以下の公式が成り立ちます。
- \(PV=\)一定
体積を変えることができる密封容器について、ふたを押すことによって体積を小さくすると、その分だけ圧力が増加することは容易に想像できます。この理由は、分子が壁に衝突する回数が増えるからです。
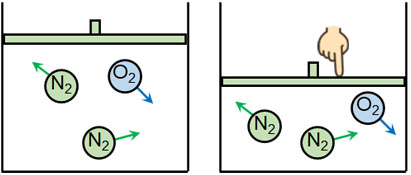
一方、容器の体積を増やすと圧力は減少します。このときボイルの法則を利用すれば、圧力と体積は反比例することがわかります。いずれにしても物質量と温度が一定なのであれば、PV(圧力と体積のかけ算)は一定になることを理解しましょう。
シャルルの法則:体積と温度の比率は一定
次にシャルルの法則を確認しましょう。シャルルの法則では、圧力と物質量が一定の場合、体積と温度は比例します。
体積を変えることができる密封容器に気体が入っているとき、温度を上げると、体積が増えることは容易に想像できます。先ほどの図を再び掲載しますが、加熱によって体積が増えるのは当然です。

体積と温度は比例するため、温度を2倍にすれば、容器の体積も2倍になります。そのため、シャルルの法則では以下の公式が成り立ちます。
- \(\displaystyle\frac{V}{T}=\)一定
この公式を覚える必要はなく、気体の状態方程式を以下のように変えることで作り出すことができます。
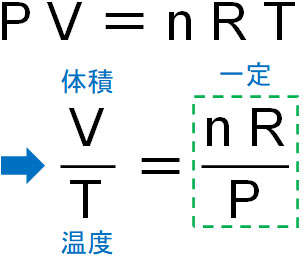
気体の状態方程式より、圧力と物質量が同じ値の場合、\(\displaystyle\frac{V}{T}=\)が一定になるのは容易に理解できます。
ボイル・シャルルの法則では2つの法則を組み合わせる
ボイルの法則とシャルルの法則を理解したら、2つの法則を組み合わせましょう。気体の状態方程式について、以下のように式を変形しましょう。

物質量が同じ場合、圧力Pと体積V、温度Tの関係は一定です。そのため、以下の公式を作ることができます。
- \(\displaystyle\frac{PV}{T}=\)一定
ボイル・シャルルの法則についても、公式を覚える必要はありません。気体の状態方程式を変形すれば公式を作れます。
ボイル・シャルルの法則を利用して計算問題を解く
理想気体であり、物質量が一定の場合は必ず\(\displaystyle\frac{PV}{T}\)が一定になります。この性質を利用して問題を解きましょう。
例えば圧力P、体積V、温度Tの状態の気体について、圧力P’、体積V’、温度T’へと変化したとします。この場合、以下の関係が成り立ちます。
- \(\displaystyle\frac{PV}{T}=\displaystyle\frac{P’V’}{T’}\)
例えば、以下の問題の答えは何でしょうか。
- 127℃、2.0L、 1.0×105Pa の気体について、27℃、3.0Lで圧力は何Paですか。
ボイル・シャルルの法則を利用して、以下のように計算しましょう。
\(\displaystyle\frac{1.0×10^5×2}{400}=\displaystyle\frac{P’×3}{300}\)
\(P’=5.0×10^4\)
こうして、圧力は5.0×104Paであるとわかります。
・ボイル・シャルルの法則を利用する
温度Tが一定のとき、変化するのは圧力Pと体積Vです(ボイルの法則)。
- \(PV=P’V’\)
また圧力Pが一定のとき、変化するのは体積Vと温度Tです(シャルルの法則)。
- \(\displaystyle\frac{V}{T}=\displaystyle\frac{V’}{T’}\)
一方で3つの値が変化するとき、ボイル・シャルルの法則を利用して計算します。
- \(\displaystyle\frac{PV}{T}=\displaystyle\frac{P’V’}{T’}\)
内容は難しくないものの、ボイル・シャルルの法則は非常に重要です。物理や化学で気体の計算問題を解くときは高頻度でボイル・シャルルの法則を利用するため、利用できるようになりましょう。
気体の状態方程式でボイル・シャルルの法則を使う
気体を取り扱うとき、必ず理解しなければいけないのが気体の状態方程式です。また物理や化学で気体の状態方程式を学んだあと、次に覚えなければいけない内容がボイル・シャルルの法則です。
ボイル・シャルルの法則について、公式を覚える必要はありません。気体の状態方程式を変形すれば、ボイルの法則やシャルルの法則に関する公式を得ることができるからです。また圧力P、体積V、温度Tを含む公式を得ることもできます。
そこでボイル・シャルルの法則を利用し、計算問題を解けるようになりましょう。概念は難しくないため、気体の状態方程式を覚えている場合、計算式を作って答えを出すことができます。
ボイル・シャルルの法則は気体の状態方程式と同様に基本的な内容です。そこで、気体の状態方程式を利用して公式を導き出せるようになりましょう。