物理や化学では気体の状態を学びます。その中でも、最も基本的な公式に気体の状態方程式があります。気体の状態方程式は必ず覚えなければいけない公式の一つです。気体の状態方程式を覚えていない場合、物理でも化学でも問題を解くことができません。
気体の状態方程式で重要な要素は圧力、体積、物質量、温度です。これらの要素が変化しても、気体の状態方程式を利用することによって計算することができます。
なお気体の状態方程式を利用すれば、状態図での蒸気圧曲線を利用して、気体の状態を計算できます。また気体の質量や分子量を計算することもできます。
気体が関わる計算をするとき、最も基本的な内容が気体の状態方程式です。そこで、どのように気体の状態方程式を利用すればいいのか解説していきます。
もくじ
理想気体:気体の拡散や圧力、状態変化
環境によって気体の状態は変化します。このとき計算を簡単にするため、私たちは気体を理想気体として扱います。分子間力(分子同士で引き合う力)や体積が0の気体を理想気体といいます。理想気体を想定する場合、気体の状態方程式を利用することができます。
気体の状態は圧力、体積、物質量、温度の4つで決まります。そこで、気体の状態方程式では4つの値を利用することで計算します。
それでは、気体の状態方程式を学ぶ前に「なぜ圧力を生じるのか」を理解しましょう。例えば空気であれば、窒素と酸素がメインで存在しています。空気による圧力というのは、「窒素分子や酸素分子が壁に衝突することによって生じる」と理解しましょう。
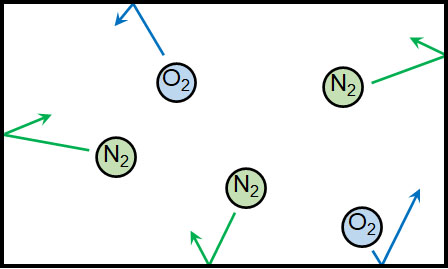
当然、一つの容器に含まれる窒素分子や酸素分子の量が多くなると、その分だけ壁に衝突する分子の量は多くなり、圧力は上昇します。また温度が高いと、分子の動きは速くなるので圧力は上昇します。容器の大きさを小さくする場合であっても、分子が壁に衝突する回数が増えて圧力が上昇します。
このように考えると、圧力というのは、気体が入っている容器の体積や気体の物質量、温度によって変化するとわかります。
通常、気体は目に見えません。そこで、分子が目に見えると仮定しましょう。分子がどれだけ壁に衝突するのかによって圧力が決まると理解すれば、気体の状態を理解するときになぜ圧力、体積、物質量、温度の4つが重要なのかわかります。
気体の状態方程式:圧力、体積、物質量、温度
気体の状態を表すとき、4つの要素が必要になることから、気体の状態方程式では圧力、体積、物質量、温度を利用します。圧力をP、体積をV、物質量をn、温度をTとすると、気体の状態方程式は以下のように表されます。
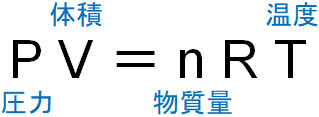
圧力の単位はPa(パスカル)、体積の単位はL(リットル)、Tの単位はK(ケルビン)です。Kは絶対温度と呼ばれており、-273℃を0Kとします。-273℃は絶対零度であり、これよりも低い温度は存在しません。つまりセルシウス温度(℃)をケルビン(K)に変換するには、273を足せばいいとわかります。例えば、27℃は300K(23+273)です。
なおRは気体定数であり、決まっている値なので重要ではありません。理想気体の場合、気体定数は必ず同じ値になります。
それでは、実際に気体の状態方程式を利用して問題を解いてみましょう。以下の答えは何でしょうか。
- 容器内に2molの気体が存在しており、温度は27℃で圧力は2.0×105Paです。理想気体と仮定する場合、容器の体積はいくらですか。なお、気体定数Rを8.3×103Pa·L/(K·mol)とします。
理想気体であるため、気体の状態方程式に値を代入することで答えを出すことができます。温度については、27℃に273を足すと300Kになるため、この数字を利用しましょう。以下のようになります。
\(2.0×10^5×V=2×8.3×10^3×300\)
\(V=24.9\)
こうして、容器の体積は24.9Lと計算できました。気体の状態方程式は必ず覚えるようにしましょう。
状態図と蒸気圧曲線:三重点と臨界点
気体の状態方程式を利用できるようになった後、状態図と蒸気圧曲線の読み方を学びましょう。気体のみで存在するのではなく、液体と気体が混ざっている場面はよくあります。このとき、圧力がどのようになっているのか把握する必要があります。
また圧力や温度によって物質の状態は変化します。例えば100℃以上の環境では水はすべて気体になりますし、0℃以下の場合だと水は固体になります。このとき、圧力と温度ごとに「物質がどのような状態で存在するのか」を表すのが状態図です。例えば以下は水の状態図です。
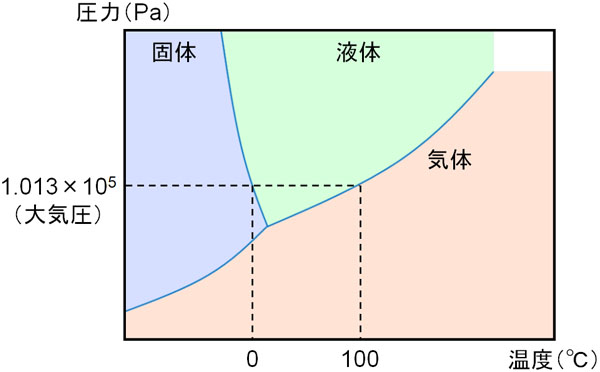
状態図では、圧力と温度のみを考えます。大気圧が1.013×105Paで一定の場合、軸を右に伸ばすと、0℃の部分で固体から液体へ変化し、100℃で液体から気体へ変化するとわかります。状態図というのは、物質の状態(固体・液体・気体)を表しているのです。
なお状態図の中でも、液体と気体の境界線を蒸気圧曲線といいます。気体の状態方程式を利用するとき、蒸気圧曲線を利用することがよくあります。そのため、状態図の中で蒸気圧曲線がどこに該当するのかわかるようにしておきましょう。
・圧力が低いと沸点が低くなる
高い山に登るとき、山頂では沸点が低くなる(90℃など)になることが知られています。この理由として、山頂では空気による圧力が低くなるからです。
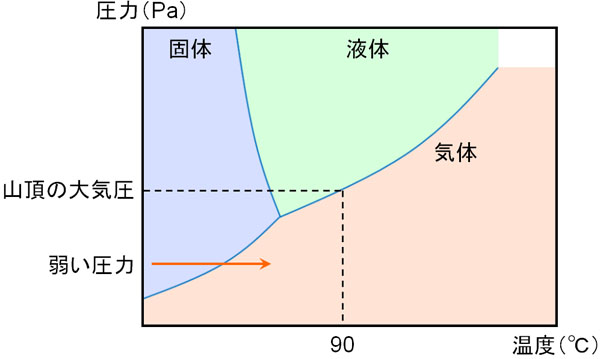
また状態図を確認すると、圧力が非常に低い環境では、水は液体にならず、固体と気体の状態のみ存在することがわかります。温度が低いと固体となり、温度が高いと気体になるのです。
・二酸化炭素の状態図
なお、分子の種類が違うと状態図が異なります。例えば二酸化炭素は液体になりません。二酸化炭素を冷やすとドライアイス(固体)になり、大気圧では液体を経ずに気体になります。
一方、圧力を高くすると二酸化炭素であっても液体になります。二酸化炭素の状態図は以下のようになります。
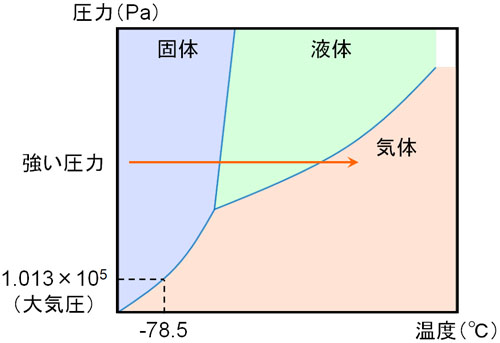
状態図を確認すれば、大気圧ではなぜ二酸化炭素が液体にならないのかわかります。
・三重点と臨界点
先ほどの状態図について、三重点と臨界点が存在します。三重点とは、固体・液体・気体の3つが重なる部分を指します。
また臨界点とは、状態図の右上に存在する部分になります。臨界点以上の圧力と温度では、液体と気体の区別がなくなります。
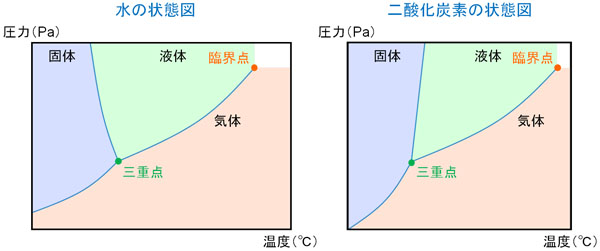
状態図の特徴を理解して、図が何を表しているのか理解しましょう。
状態図での飽和蒸気圧と気体平衡
それでは、気体の状態方程式でなぜ状態図を学ぶことが重要になるのでしょうか。それは、蒸気圧曲線を利用することによって計算することがひんぱんにあるからです。
気体が存在するとき「気体のみの状態で存在しているとき」と「液体と気体の両方が存在しているとき」の2パターンがあります。容器の中に気体のみが存在している場合、気体の状態方程式を利用して計算できます。一方、液体と気体の両方が容器に入っている場合、蒸気圧を考慮しましょう。
蒸気圧とは、蒸気として存在する物質がどれだけの圧力を有するのかを示します。容器の中に水を入れるとき、常温であっても水は液体で存在することがあれば、気体で存在することもあります。このとき、容器内の気体の圧力を表すのが蒸気圧です。
水の状態図から、蒸気圧曲線と温度を取り出した図が以下になります。
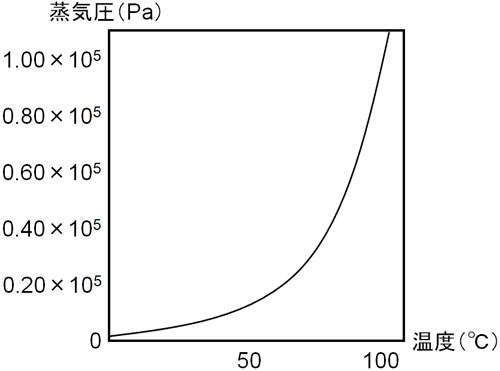
自由に体積を変えることのできる密封容器に水を入れる場合、容器の体積は温度によって変化します。温度が高い場合、より多くの液体が蒸気(気体)へ変化することによって圧力が上昇し、容器の体積は大きくなります。
空気(窒素や酸素など)による容器の内圧と外圧は同じです。ただH2Oが蒸気になる分だけ内圧が上昇するため、容器の体積が増えるのです。
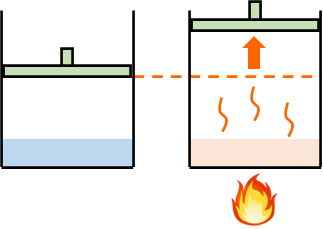
一方、温度が低いと蒸気圧は低くなり、水は蒸気(気体)から液体へと変化することで、容器内の圧力は減少します。その結果、容器の体積は減少します。これらの現象については、問題なく理解できると思います。
容器の中に液体が存在するとき、必ず気体平衡の状態になっています。例えば水の気体平衡では、気体から液体に変わる水と、液体から気体へ変わる水の量が等しくなっています。気体平衡のときの蒸気圧を飽和蒸気圧といいます。
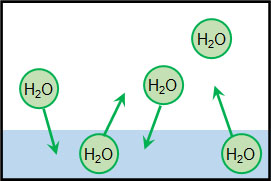
飽和蒸気圧(蒸気圧)は温度に依存します。このとき、気体の状態方程式を利用することによって、蒸気(液体から気体になった水)の圧力を計算できます。以下の公式を利用します。
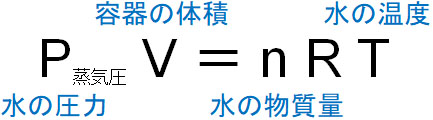
つまり水が液体で存在する場合、蒸気(気体の水)の圧力(飽和蒸気圧)というのは、気体の状態方程式を利用することによって計算できるのです。
蒸気圧曲線と状態方程式を使って計算する
それでは、液体と気体の両方が存在する場合について、気体の状態方程式を利用して計算をしてみましょう。以下の問題の答えは何でしょうか。
- 体積を変えることのできる密封容器に気体の物質が0.1molあります。温度が常に27℃に保たれ、この物質の飽和蒸気圧は4.0×104Paです。また気体定数Rを8.3×103Pa·L/(K·mol)、有効数字3ケタとします。
- 密封容器の体積が10Lの場合、気体の圧力はいくらでしょうか。
- 容器の体積を小さくすると、液体を生じました。このときの容器の体積はいくらでしょうか。
- 容器の体積を2Lにするとき、容器内に存在する液体の物質量はいくらでしょうか。なお、物質は気体または液体でのみ存在します。
それぞれの問題について、気体の状態方程式を利用して解きましょう。
1)
容器の体積(10L)、物質量(0.1mol)、温度(300K:27+273)がわかっているため、気体の状態方程式に代入することで答えを得ることができます。
\(10P=0.1×8.3×10^3×300\)
\(P=2.49×10^4\)
こうして、気体の圧力は2.49×104Paとわかります。また飽和蒸気圧4.0×104Paよりも低い値であるため、すべて気体で存在しています。
2)
前述の通り、密封容器に液体が存在する場合、必ず気体平衡の状態となっています。つまり、「気体の蒸気圧=飽和蒸気圧」です。
密閉容器の体積を小さくする場合、当然ながら圧力は大きくなります。また、容器内の圧力が飽和蒸気圧よりも大きくなった場合、気体として存在していた物質は液体になります。以下のように、圧力が高くなることで気体から液体へ移るのです。
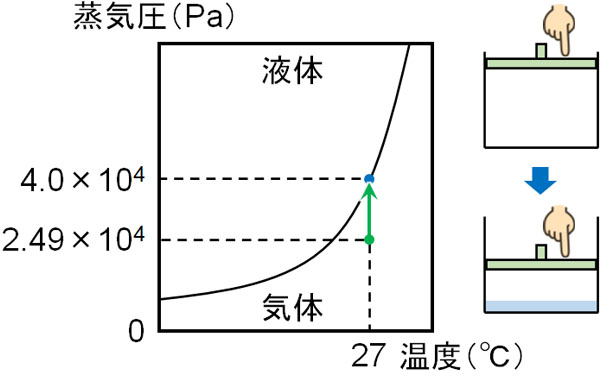
つまり液体を生じたときの圧力とは、飽和蒸気圧である4.0×104Paを意味しています。また物質量0.1mol、温度300Kであるため、気体の状態方程式を利用して体積を計算しましょう。
\(4.0×10^4×V=0.1×8.3×10^3×300\)
\(V=6.225\)
\(V≒6.23\)
こうして、溶液の体積が6.23Lのときに液体を生じるようになるとわかります。
3)
前述の通り、気体と液体が存在する場合では飽和蒸気圧が同じです。そのため、圧力は4.0×104Paです。また温度は300Kで一定です。一方、気体として存在していた物質は一部が液体になります。そこで容器の体積を2Lにするとき、気体の物質量をn’として計算しましょう。
\(4.0×10^4×2=n’×8.3×10^3×300\)
\(n’≒0.0321\)
こうして、0.0321molの物質が気体で存在するとわかりました。元々は0.1molであったため、液体になった物質は0.0679molです。
\(0.1-0.0321=0.0679\)
こうして、6.79×10-2molが正解であるとわかります。
気体の質量・分子量・密度を利用して計算する
なお気体の状態方程式を利用するとき、気体の質量や分子量、密度を利用して計算することもあります。方法は簡単であり、新たな公式を覚える必要もありません。気体の状態方程式を変えることによって、気体の質量や分子量、密度を用いた計算ができるようになります。
まず、質量と分子量に着目しましょう。質量をw(g)、分子量をMとすると、物質量nというのは以下の式で表されます。
- \(n=\displaystyle\frac{w}{M}\)
物質量の計算は化学の初歩であるため、これについては問題ないはずです。つまりnを\(\displaystyle\frac{w}{M}\)へ変換することにより、気体の状態方程式を以下のように表すことができます。

または、密度d(g/L)を利用して気体の状態方程式を表すこともできます。質量w(g)を体積V(L)で割れば、気体の密度になります。そのため、以下のように式を変形できます。
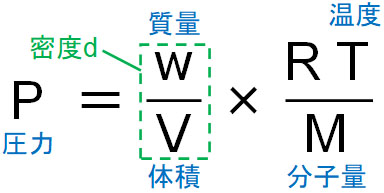
これらの公式を覚える必要はなく、気体の状態方程式を利用して作れるようにしましょう。そうすれば、覚えなくても式を導き出せるようになります。
それでは、次の問題を解いてみましょう。
- 温度が27℃、気体定数Rが8.3×103Pa·L/(K·mol)のとき、以下の分子の分子量を答えましょう。
- 圧力が1.0×105Pa、容器の体積が16.6Lのとき、質量が40gの気体
- 圧力が8.3×104Paのとき、密度が3g/Lの気体
1)
先ほどの気体の状態方程式に代入すれば、答えを得ることができます。
\(1.0×10^5×16.6=\displaystyle\frac{40}{M}×8.3×10^3×300\)
\(M=60\)
こうして、分子量は60とわかりました。
2)
同様に、気体の状態方程式に代入しましょう。
\(8.3×10^4=3×\displaystyle\frac{8.3×10^3×300}{M}\)
\(M=90\)
こうして、分子量は90とわかりました。
気体の状態方程式を覚えている場合、質量や分子量、密度を含む公式に変換するのは簡単です。そこで、気体の質量や分子量、密度を用いる場合についても計算できるようになりましょう。
気体の状態方程式を利用して計算する
気体を取り扱うとき、物理でも化学でも非常に重要になるのが気体の状態方程式です。気体の状態方程式を覚えていない場合、問題を解くことはできません。一方、一つの公式を覚えていれば多くの問題を解けるようになります。
なお気体に加えて液体が存在する場合、蒸気圧が重要になります。そこで状態図を確認し、飽和蒸気圧を利用することで気体の圧力を確認しましょう。
また気体の状態方程式を使うとき、気体の質量や分子量、密度を利用して計算することもあります。このときは気体の状態方程式を変形することで計算しましょう。
物理や化学で気体を学ぶとき、最も基本的な内容が気体の状態方程式です。そこで、気体の状態方程式を利用できるようになりましょう。






