分圧の法則と全圧：混合気体の圧力とモル分率を利用した計算

気体を学ぶとき、圧力を取り扱います。気体の圧力は分子ごとに分けることができます。すべての気体の圧力を全圧と呼ぶのに対して、分子ごとの圧力を分圧といいます。

空気のように、複数の気体が混ざっている場面はよくあります。そこで混合気体の計算をするとき、分圧を利用すると効果的です。

分圧の計算ではドルトンの分圧の法則を利用します。分圧というのは、足し算によって計算できます。また分圧は物質量に依存するため、モル分率を利用することによって分圧の計算が可能です。

それでは、どのように分圧の計算をすればいいのでしょうか。ここでは複数の気体が混ざっているときについて、圧力の計算方法を解説していきます。

全圧と分圧の違い

気体の状態方程式を学ぶ場合、全圧を用いて計算します。例えば空気の圧力を計算するのは、全圧を計算するのと意味が同じです。すべての分子について、圧力を足した値が全圧です。

一方、分圧とは何でしょうか。空気であれば、窒素と酸素で主に構成されています。つまり大気圧（空気の圧力）というのは、窒素と酸素による圧力と考えることができます。

• 空気の圧力（全圧）：窒素と酸素の両方による圧力
• 分圧：窒素の圧力、酸素の圧力

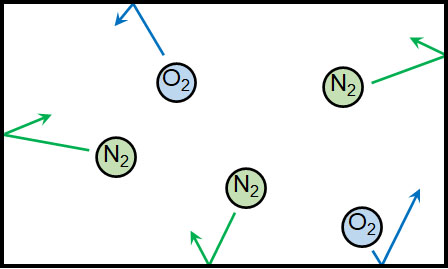
つまり、分子ごとの圧力が分圧です。空気の圧力について、窒素の圧力は分圧ですし、酸素の圧力も分圧です。

ドルトンの分圧の法則：圧力は足し算できる

重要なのは、分圧を分けて計算できることです。例えば窒素と酸素のみが存在する場合、以下の足し算によって全圧の計算ができます。

• 全圧 ＝ 窒素の分圧 ＋ 酸素の分圧

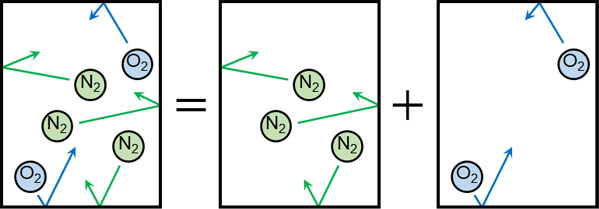
混合気体の圧力（全圧）というのは、それぞれの気体の圧力を足すことによって計算できます。これをドルトンの分圧の法則といいます。

例えば気体A（圧力はP_A）、気体B（圧力はP_B）、気体C（圧力はP_C）が混ざっている場合、全圧Pは以下の計算式になります。

• \(P=P_A+P_B+P_C\)

なお、それぞれの圧力は体積Vや物質量n、温度Tがわかれば計算できます。そこでそれぞれの分圧を計算し、足すことによって全圧の計算が可能になるのです。

例えば、以下の問題の答えは何でしょうか。

• 8.3Lの容器に窒素2.0molと酸素1.0molが入っています。温度が27℃のとき、全圧（P）とそれぞれの気体の分圧（窒素：P₁、酸素：P₂）はいくらでしょうか。なお、気体定数Rを8.3×10³Pa·L/(K·mol）とします。

気体の状態方程式を利用して問題を解くと以下のようになります。

・窒素の分圧

\(8.3P_1=2×8.3×10^3×300\)

\(P_1=6.0×10^5\)

・酸素の分圧

\(8.3P_2=1×8.3×10^3×300\)

\(P_2=3.0×10^5\)

・全圧

\(P=6.0×10^5+3.0×10^5\)

\(P=9.0×10^5\)

気体の状態方程式を利用して圧力を計算すればいいため、分圧の計算問題を解くのは難しくありません。

分圧には飽和蒸気圧も関係している

なお気体の圧力を学ぶとき、状態図（蒸気圧曲線）を利用する問題を解くことがよくあります。蒸気圧というのは、分圧と同じと理解しましょう。

窒素や酸素の場合、常温では常に気体です。一方、物質によっては温度によって自由に液体や気体になるケースがあります。この代表例が水です。

液体の水を密封容器に入れるとき、水分子は液体だけで存在しているわけではなく、気体（水蒸気）としても存在します。また密封容器に液体の水が存在する場合、必ず気体平衡となっており、水は液体になったり気体になったりしています。

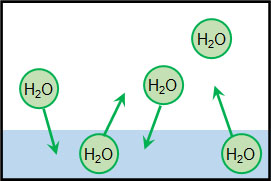
容器について、外側からは空気（窒素と酸素）が容器を押しています。一方で容器の内側からは、空気（窒素と酸素）による圧力だけでなく、水蒸気（気体の水）による分圧も発生しています。気体の水についても、壁に衝突することで圧力を生じるのです。

飽和蒸気圧の計算をするというのは、言い換えると水蒸気（気体の水）の分圧を計算するのと意味が同じです。すべての気体の圧力というのは、蒸気圧も含めて計算するようにしましょう。例えば、以下の問題の答えは何でしょうか。

• ある気体を水上置換で集めました。容器と水槽で水位を合わせ、容器内の体積を測定すると8.3Lでした。大気圧が9.96×10⁴Paであり、27℃での水の飽和蒸気圧を3.6×10³Paとします。気体定数Rが8.3×10³Pa·L/(K·mol）であり、27℃で測定している場合、気体の分圧と物質量はいくらでしょうか。

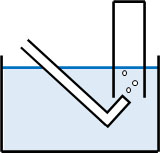
気体を水上置換で集めているというのは、要は密封容器に水が存在している状態と同じと考えましょう。つまり、密封容器に水（液体）と発生させた気体が存在しています。

また液体の水が存在するため、一部は蒸気（気体の水）で存在しています。そのため発生した気体の分圧と水蒸気の分圧（気体の水の圧力）を足すと、容器内の気体の圧力になります。容器内の圧力は大気圧と釣り合っているため、求める気体の分圧をPとして以下の式を作りましょう。

\(9.96×10^4=P+3.6×10^3\)

\(P=9.6×10^4\)

こうして、気体の分圧は9.6×10⁴Paとわかりました。

気体の分圧がわかれば、気体の物質量の計算が可能です。容器の体積は8.3L、温度は300Kであるため、気体の状態方程式に値を代入することで物質量（n）を計算しましょう。

\(9.6×10^4×8.3=n×8.3×10^3×300\)

\(n=0.32\)

こうして、気体の物質量は0.32molとわかります。

圧力は物質量に依存し、モル分率による計算が可能

次に、物質量を利用することによって圧力を計算しましょう。圧力を生じる理由は、気体が壁に衝突するからです。つまり分子が壁に衝突する回数が多いほど圧力が大きくなります。

容器内に存在する気体の物質量が少ない場合、圧力は小さいです。また容器内に多くの分子が存在する場合、圧力は大きくなります。圧力の大小というのは、容器内に存在する分子の物質量に依存するのです。

つまり分圧というのは、どれだけ多くの分子が存在するのかによって決まります。より詳しくいうと、モル分率（モル濃度の比率）によって分圧の計算が可能です。

例えば圧力が9.0×10⁴Paであり、窒素分子が2mol、酸素分子が1mol存在する場面を考えてみましょう。窒素分子と酸素分子の物質量の割合は2：1です。これはつまり、窒素と酸素の分圧が2：1であることを意味しています。

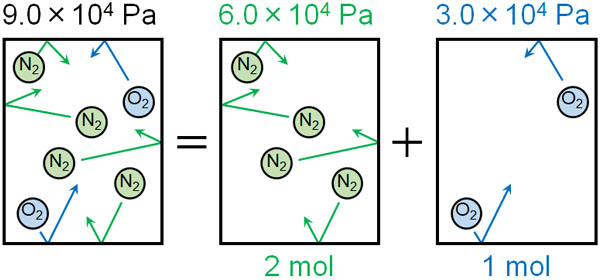
そのため全圧が9.0×10⁴Paなのであれば、窒素の分圧は6.0×10⁴Paであり、酸素の分圧は3.0×10⁴Paです。気体の圧力は「分子がどれだけの割合で容器内に存在するのか」で決まるため、物質量の割合（モル分率）が重要になるのです。

・モル分率を利用して圧力を得る

なおモル分率がわかっているのであれば、モル分率を利用してほかの気体の分圧を計算することができます。モル濃度の割合に応じて分圧が決まるため、モル分率を利用することで圧力を得られるのです。

例えば窒素分子が3mol、酸素分子が1mol存在する場合、混合気体のモル分率は窒素が\(\displaystyle\frac{3}{4}\)、酸素が\(\displaystyle\frac{1}{4}\)です。つまり全圧に対して、窒素の分圧は\(\displaystyle\frac{3}{4}\)ですし、酸素の分圧は\(\displaystyle\frac{1}{4}\)です。

また窒素と酸素の割合は3：1であるため、窒素の分圧を\(\displaystyle\frac{1}{3}\)倍すれば、酸素の分圧を得ることができます。当然、酸素の分圧を3倍すれば窒素の分圧になります。分圧の計算では、分圧と物質量の比は同じになります。

圧力と物質量の関係を数式で表す

それでは、圧力と物質量の関係を数式で表してみましょう。全圧をP、分子Aの分圧をP_A、分子Bの分圧をP_Bとします。また、分子Aの物質量をn_A、分子Bの物質量をn_Bとします。圧力と物質量の比は同じなので、以下の関係が成り立ちます。

• \(P:P_A:P_B=(n_A+n_B):n_A:n_B\)

教科書では最初にこのような数式が提示されるため、理解しにくいです。ただここまでの内容を学び、圧力と物質量の比が同じであると理解すれば、数式の意味を把握するのは簡単です。

また物質量の割合（モル分率）を計算すると、分子Aは\(\displaystyle\frac{n_A}{n_A+n_B}\)であり、分子Bは\(\displaystyle\frac{n_B}{n_A+n_B}\)です。そのため全圧Pを利用して、以下のように分圧を計算できます。

• \(P_A=P×\displaystyle\frac{n_A}{n_A+n_B}\)
• \(P_B=P×\displaystyle\frac{n_B}{n_A+n_B}\)

これらの数式を覚える必要はありません。圧力と物質量の比が同じであることを理解すれば、ここまで解説した式を作れるようになります。

2気体が存在するとき、分圧の計算を行う

それでは、2気体が存在するときの分圧の計算をしてみましょう。以下の問題の答えは何でしょうか。

• コックが閉じた状態にて、9.0Lの容器Xに4.0×10⁵Paの窒素、3.0Lの容器Yに4.0×10⁵Paの酸素が入っています。温度を一定に保ってコックを開くとき、「それぞれの気体の分圧」と「窒素と酸素の物質量の割合」を計算しましょう。

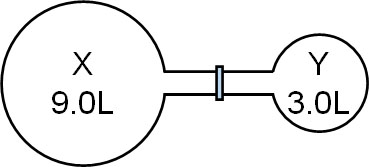
コックを開ける場合、変化するのは容器の体積です。温度は一定であるため、窒素の分圧をP_A、酸素の分圧をP_Bとすると、ボイルの法則を利用して以下のように分圧を計算できます。

・P_Aの計算

\(4.0×10^5×9=P_A×12\)

\(P_A=3.0×10^5\)

窒素の分圧は3.0×10⁵Paと計算できます。

・P_Bの計算

\(4.0×10^5×3=P_B×12\)

\(P_B=1.0×10^5\)

酸素の分圧はと1.0×10⁵Paと計算できます。

・窒素と酸素の物質量の割合

なお、分圧の割合は物質量の割合と同じになります。そのため窒素の物質量をn_A、酸素の物質量をn_Bとしたとき、窒素と酸素の物質量の割合は以下のように計算できます。

\(n_A:n_B=3.0×10^5:1.0×10^5=3:1\)

分圧の性質を利用して計算する

複数の気体が混ざっていることはよくあります。混合気体について、すべての分圧を足すと全圧になります。

ドルトンの分圧の法則を利用して分圧や全圧の計算をしましょう。分子ごとに圧力を計算し、足せばいいとわかれば、分圧や全圧の概念は難しくありません。なお分圧には飽和蒸気圧も関わるため、液体（水など）が気体になるときの圧力を計算できるようになりましょう。

また気体の分圧は物質量に依存します。物質量が多いほど、分圧も大きくなります。分圧と物質量の比率は同じであるため、モル分率を利用することによって分圧や全圧の計算が可能です。

分圧の性質を理解すれば、新たな公式を覚えなくても計算問題を解けるようになります。分圧の性質を利用して、そのつど計算式を作れるようになりましょう。