ばねなど、同じ動きを繰り返す運動を単振動といいます。単振動の計算ではsinθまたはcosθを利用することで変位や速度、加速度を得ることができます。
物理で単振動を学ぶとき、公式を覚えてはいけません。そうではなく、公式を作れるようにしましょう。単振動は公式を覚えてはいけない学習内容です。
なお単振動では、運動方程式を作るときにマイナスを加える必要がありますし、振り子による運動を単振動とみなすこともあります。これらの理由を学んでいないと、単振動の問題を解くときに式を作ることができません。
それでは単振動の計算問題を解くとき、どのように公式を利用すればいいのでしょうか。単振動の概念や公式の意味、式の作り方を解説していきます。
もくじ
復元力が働く運動が単振動
まず、単振動とは何かを理解しましょう。単振動とは、元の位置に戻ろうとする力(復元力)が働く運動です。
単振動でひんぱんに利用される例がばねです。ばねを引っ張る(または縮める)ことにより、ばねはエネルギーをもつことになります。その後、ばねを離すと、ばねは伸び縮みを繰り返します。摩擦力や空気抵抗が存在しない場合、ばねはずっと同じ振動を繰り返します。

単振動を理解するため、実際にばねが動いている場面を想像しましょう。上図のように、ばねは自然長から同じ長さで伸びたり縮んだりを繰り返します。ばねのように、同じ動きを繰り返すと単振動になります。
ばねの弾性力は\(F=kx\)で表すことができます。そのため復元力が働くとき、反対方向で同じ力が加わることになります。復元力は\(F=-Kx\)で表されます。\(K\)は正の定数です。また戻るときに働く力が復元力であるため、力の方向は反対です。そのため、マイナスを加えます。
単振動による速度と加速度の関係
それでは、物体が単振動するときの速さと加速度はどのようになるでしょうか。先ほどの図(ばねを水平方向に取り付けている図)について、スローモーションでばねが振動している場面を想像しましょう。
速度\(v\)について、物体の速さは左端と右端で0になります。ばねの伸び(または縮み)が最大になると、物体は止まるので当然ながら速さはゼロです。また、ばねが自然長になると速さは最大になります。
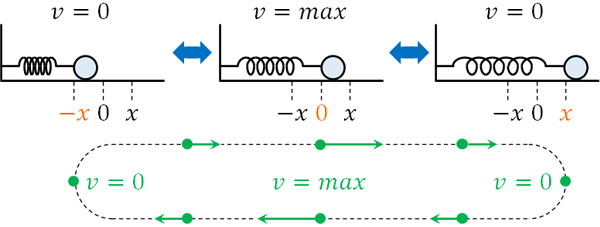
一方で加速度\(a\)はどうでしょうか。ばねの自然長に対して、物体が左側にあるのか、それとも右側にあるのかによって加速度の向きが異なります。
物体が右側にある場合、ばねによる力によって左向きの力が加わります。つまり、加速度は左向きです。当然、自然長との距離が大きいほど加速度は大きくなります。また物体が左側にある場合、加速度は右向きになります。

つまり、ばねの伸びまたは縮みが最大のとき、加速度の大きさは最大になります。またばねが自然長のとき、加速度はゼロになります。単振動では、速さと加速度でこのような違いがあることを理解しましょう。
単振動の変位・速さ・加速度の公式
ここまでの内容を理解したうえで、単振動の変位(位置)や速さ、加速度を計算する公式を学びましょう。
単振動を学ぶとき、絶対にしてはいけないのが公式の暗記です。理由としては、暗記しても問題を解くことができないからです。単振動の場合、問題文が違えばあなたが作るべき式が変わります。
単振動の計算では、sinθまたはcosθを利用します。このときsinθを利用するのか、それともcosθを利用するのかは問題文によって変わります。場合によっては、式にマイナスを加えることもあります。これが、公式を覚えても意味がない理由です。そこで、公式を作れるようになりましょう。
単振動で最も重要な概念に「等速円運動を横から見ると単振動になる」ことが挙げられます。
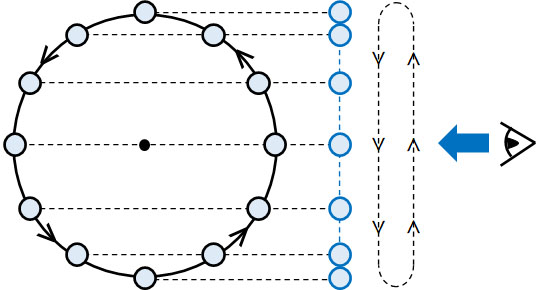
単振動というのは、等速円運動でたて軸だけに着目した運動を指します。等速円運動を横から見るというのは、横軸を考慮せず、たて軸のみで変位や速さ、加速度を計算することを意味するのです。
また単振動では、振動するときの幅が決まっています。sinθとcosθでは、最大値は1であり、最小値は-1です。そのためsinθまたはcosθを利用することにより、単振動での振幅を表現できるのです。単振動は振幅が一定であるため、等速円運動を利用するのが最適です。
なお等速円運動を利用して単振動の公式を得るため、等速円運動を学んでいない場合、単振動を理解することはできません。そのため、必ず事前に等速円運動の性質や角速度の概念、公式の導き出し方を学ぶ必要があります。
単振動で変位\(x\)を得る公式
それでは、単振動を学ぶときに物理の教科書に記載されている公式の導出を行いましょう。前述の通り公式を覚える必要はなく、公式の作り方を学ぶのです。
単振動での変位(距離)というのは、自然長からどれだけ離れているのかを意味します。等速円運動では、円の中心からたて軸方向へどれだけ進んでいるのかを計算しましょう。
そこで、等速円運動の半径を\(A\)とします。つまり、振幅\(A\)が等速円運動での半径に該当します。また角速度ωについて、\(t\)秒後の角度θは\(ωt\)です。そのため、円の中心からたて軸方向への距離\(x\)は以下の公式によって得られます。
- \(x=Asinωt\)
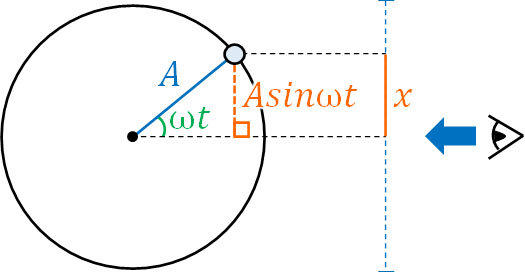
斜辺と角度を利用して直角三角形のたての長さを出せばいいため、単振動の変位を得るのは難しくありません。
単振動で速さ\(v\)を得る公式
次に単振動で速さ\(v\)を得る公式を導き出しましょう。等速円運動の公式より、\(v=rω\)です。つまり円の半径\(r\)と角速度ωをかけることによって速さ\(v\)を計算できます。前述の通り、単振動では円の半径\(r\)の代わりに振幅\(A\)を利用します。そのため、\(v=Aω\)を利用しましょう。
また等速円運動のたて軸方向の速さ\(v\)を得るためには、\(v=Aω\)に\(cosωt\)をかければいいです(\(θ=ωt\))。
- \(v=Aωcosωt\)
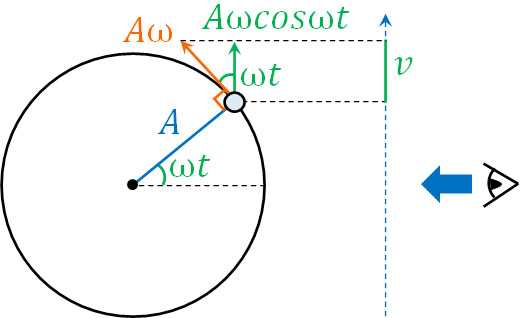
等速円運動の速さを計算した後、角度(\(θ=ωt\))を利用してたて軸の長さの計算をすればいいため、単振動の速さを得る公式の導出も難しくありません。
単振動で加速度\(a\)を得る公式
それでは、加速度\(a\)はどのように計算すればいいのでしょうか。円運動をしている物体には、円の中心に向かって加速度を生じています。このときの加速度は等速円運動の公式より、\(a=rω^2\)となります。
ただ単振動では振幅\(A\)を利用するため、\(a=Aω^2\)に変えましょう。また角度\(ωt\)を利用してたて軸の長さを計算すると、以下のように単振動での加速度を得られます。
- \(a=Aω^2sinωt\)
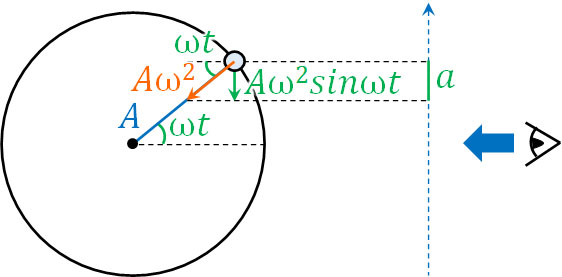
ただ単振動の加速度では、変位や速度に対して、常に向きが反対です。例えば上方向を正とすると、加速度は反対向きになっています。そこで単振動で加速度を計算するとき、ベクトル(運動の向き)を考慮してマイナスを加えましょう。つまり、以下が単振動での加速度の公式です。
- \(a=-Aω^2sinωt\)
なお\(x=Asinωt\)であるため、\(x=Asinωt\)を代入すると以下の式になります。
- \(a=-ω^2x\)
単振動の加速度を計算するとき、2つの方法があることを覚えましょう。なお前述の通り、単振動の公式は覚える必要がありません。ただ\(a=-ω^2x\)については、角振動数や周期を出すときに必要なので覚えるといいです。
公式を覚えるのは意味がない:sinθとcosθの両方が利用される
それでは、なぜ変位や速さ、加速度の公式を覚える意味がないのでしょうか。それは、前述の通り問題文によってsinθではなくcosθを利用しなければいけないことがあるからです。また先ほどの公式に対して、マイナスを加えるケースもあります。この理由を理解するため、変位を利用して解説していきます。
先ほど、単振動の変位が0となる場所をスタート地点としました。言い換えると、ばねの自然長がスタート地点です。
ただ、変位0からスタートするとは限りません。例えば、ばねを伸ばした状態から手を離す場合、ばねの変位が最大値(自然長から最も伸びた状態)からスタートします。この場合、変位は最大値からスタートすることになります。
角度が0°のときに変位が最大になる必要があるため、変位の計算ではsinθではなくcosθを利用します。\(cos0°=1\)だからです。この場合、あなたが作る式は以下になります。
- \(x=Acosωt\)
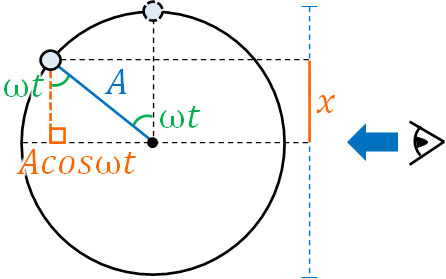
一方、ばねを縮める場合はどうでしょうか。この場合、上方向を正とすると、変位はマイナスの位置からスタートすることになります。そのため変位の計算ではcosθを利用し、さらにはマイナスを加える必要があります。
- \(x=-Acosωt\)
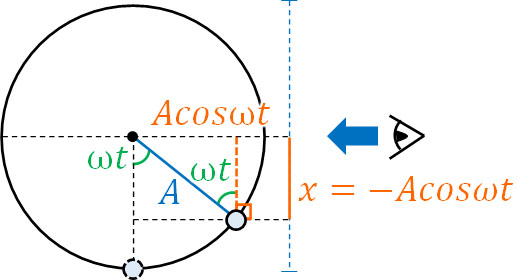
このように、スタート地点によって利用するべき計算式が変わります。当然、同じことは速さや加速度を得るときも起こります。これが、単振動を学ぶときに公式を暗記してはいけない理由です。
公式を覚えても計算問題を解くことはできません。そこで公式を覚えず、公式の作り方を学びましょう。これにより、すべての応用問題を解けるようになります。
単振動の運動方程式の立て方:角振動数と周期の公式
次に単振動の運動方程式を作れるようになりましょう。運動方程式は\(F=ma\)であるため、力の大きさ\(F\)と加速度\(a\)がわかれば、運動方程式を立てることができます。
・角振動数ωを得る公式
復元力が働く運動を単振動と解説しました。復元力は前述の通り\(F=-Kx\)であるため、復元力を基準にすると、\(F=ma\)を以下の式に変形できます。
- \(-Kx=ma\)
また単振動では、前述の通り\(a=-ω^2x\)です。そのため、運動方程式は以下のようになります。
- \(-Kx=m(-ω^2x)\)
そこで式をさらに変形すると、以下のようになります。
\(-Kx=m(-ω^2x)\)
\(K=mω^2\)
\(ω^2=\displaystyle\frac{K}{m}\)
\(ω=\sqrt{\displaystyle\frac{K}{m}}\) (\(ω>0\))
こうして、公式として\(ω=\sqrt{\displaystyle\frac{K}{m}}\)を得ることができました。等速直線運動では、角速度がωです。それに対して、単振動ではωを角振動数といいます。名前は異なるものの、同じ概念です。
なお角振動数の公式を覚える必要はなく、\(F=ma\)を利用して\(-Kx=m(-ω^2x)\)を作り、式を計算しましょう。
・周期\(T\)を得る公式
次に周期\(T\)を計算しましょう。等速直線運動で一周するために必要な時間が\(T\)です。等速円運動で角速度(1秒間で進む角度)がωなのであれば、\(360°=2π\)であるため、以下の式を作れます。
\(ωT=2π\)
\(T=\displaystyle\frac{2π}{ω}\)
また角速度(角振動数)は\(ω=\sqrt{\displaystyle\frac{K}{m}}\)であるため、先ほどの式に代入しましょう。
- \(T=2π\sqrt{\displaystyle\frac{m}{K}}\)
こうして、周期\(T\)を得る公式を導くことができました。この公式についても覚える必要はなく、\(ωT=2π\)と\(ω=\sqrt{\displaystyle\frac{K}{m}}\)を利用してそのつど計算しましょう。
水平ばね振り子による単振動
それでは、単振動に関する練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
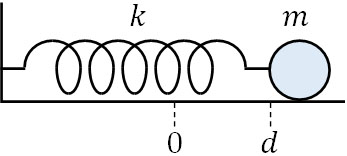
- 下図のように、ばね定数\(k\)のばねを壁に固定し、質量\(m\)の物体を付けてなめらかな床に置きます。ばねを自然長から\(d\)伸ばして離し、この瞬間を時間\(t=0\)とします。物体が初めて\(\displaystyle\frac{d}{2}\)を通過するとき、速度、加速度、時間を求めましょう。なお、ばねが伸びる方向(図の右側)を正とします。
・速度の計算
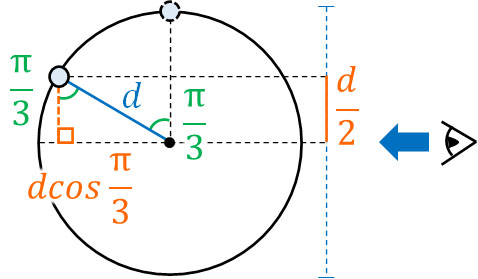
物体のスタート地点は変位(距離)が最大値の場所です。また\(\displaystyle\frac{d}{2}\)を通過するとき、距離は最大値の\(\displaystyle\frac{1}{2}\)になっているため、角度は\(\displaystyle\frac{π}{3}\)(60°)です。
下図より、\(\displaystyle\frac{d}{2}=dcos\displaystyle\frac{π}{3}\)であるため、角度は\(\displaystyle\frac{π}{3}\)で問題ないとわかります。
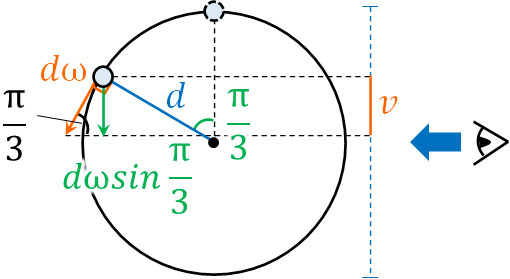
それでは、等速直線運動で角度が\(\displaystyle\frac{π}{3}\)のとき、速さ\(v\)はいくらでしょうか。等速円運動の公式\(v=rω\)と角度を利用すると、以下のようになります。
\(v=dωsin\displaystyle\frac{π}{3}\)
\(v=dω\displaystyle\frac{\sqrt{3}}{2}\)
なお速度は上向きとは反対方向であるため、\(v=-dω\displaystyle\frac{\sqrt{3}}{2}\)に変えましょう。角振動数ωはわかっていないものの、ひとまず\(v=-dω\displaystyle\frac{\sqrt{3}}{2}\)となります。
・加速度の計算
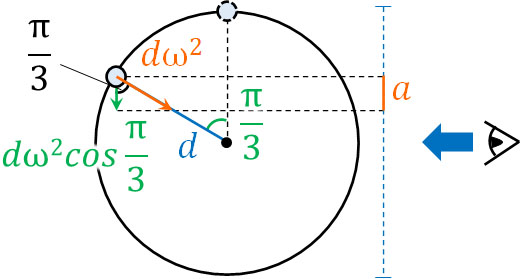
次に加速度の計算をしましょう。等速円運動の公式\(a=rω^2\)より、\(a=dω^2\)を利用すると以下のようになります。
\(a=dω^2cos\displaystyle\frac{π}{3}\)
\(a=\displaystyle\frac{dω^2}{2}\)
なお加速度は上向きとは反対方向なので、\(a=-\displaystyle\frac{dω^2}{2}\)へ変えましょう。こうして、\(a=-\displaystyle\frac{dω^2}{2}\)となります。
・角振動数ωを計算し、速度と加速度を得る
次に角振動数ωを計算しましょう。ばね定数は\(k\)であり、伸ばしているばねの距離は\(d\)なので、復元力は\(F=-kd\)です。そのため、運動方程式は以下のようになります。
\(-kd=ma\)
この式はばねを\(d\)伸ばすときの運動方程式であり、加速度は最大である\(a=-dω^2\)です(等速円運動の公式より)。そのため、以下のように角振動数ωを計算できます。
\(-kd=m×-dω^2\)
\(ω^2=\displaystyle\frac{k}{m}\)
\(ω=\sqrt{\displaystyle\frac{k}{m}}\) (\(ω>0\))
角振動数ωの計算方法は先ほど解説した通りなので、同じ方法で計算しましょう。また角振動数ωがわかれば、速度と加速度を計算できます。
\(v=-dω\displaystyle\frac{\sqrt{3}}{2}\)
\(v=-d·\sqrt{\displaystyle\frac{k}{m}}·\displaystyle\frac{\sqrt{3}}{2}\)
\(v=-\displaystyle\frac{d}{2}·\sqrt{\displaystyle\frac{3k}{m}}\)
こうして、速度は\(v=-\displaystyle\frac{d}{2}·\sqrt{\displaystyle\frac{3k}{m}}\)と計算できました。同様に加速度を計算しましょう。
\(a=-\displaystyle\frac{dω^2}{2}\)
\(a=-\displaystyle\frac{d}{2}×\displaystyle\frac{k}{m}\)
\(a=-\displaystyle\frac{kd}{2m}\)
加速度は\(a=-\displaystyle\frac{kd}{2m}\)とわかりました。
・時間\(t\)の計算
\(t\)秒で進む角度は\(\displaystyle\frac{π}{3}\)であるため、\(ωt=\displaystyle\frac{π}{3}\)です。また\(ω=\sqrt{\displaystyle\frac{k}{m}}\)なので、以下のように計算しましょう。
\(ωt=\displaystyle\frac{π}{3}\)
\(\sqrt{\displaystyle\frac{k}{m}}t=\displaystyle\frac{π}{3}\)
\(t=\displaystyle\frac{π}{3}·\sqrt{\displaystyle\frac{m}{k}}\)
こうして、経過時間は\(t=\displaystyle\frac{π}{3}·\sqrt{\displaystyle\frac{m}{k}}\)と計算できました。
振り子の単振動(単振り子):角振動数と周期の計算方法
単振動と同時に学ぶ内容に振り子の単振動(単振り子)があります。振り子の軌道は弧を描くものの、触れる角度の小さい振り子運動については、横の振動をしていると捉えることができます。

つまり振り子の動きを単振動と捉えることができるのです。この場合、重りは水平方向で横に振動しているとみなせます。
このとき、糸と鉛直方向との角度をθとすると、振り子による軌道の接線方向に働く力は\(mgsinθ\)です。つまり、水平方向に\(F=mgsinθ\)の力が働いています。
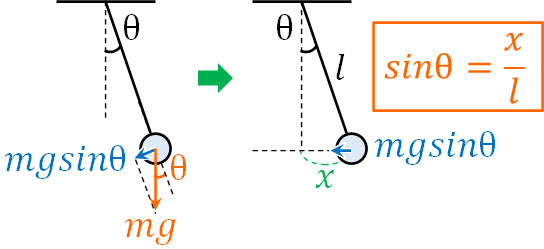
また図より、糸の長さを\(l\)、中央から横軸方向の距離を\(x\)とすると、\(sinθ=\displaystyle\frac{x}{l}\)です。そのため、単振り子での水平方向の力(復元力)は以下のように表すことができます。
- \(F=-\displaystyle\frac{mgx}{l}\)
右向きを正とする場合、左向きの力である復元力は負であるため、マイナスを加えます。
また\(F=ma\)であり、振り子による運動を単振動とみなすので、前述の解説より\(a=-ω^2x\)です(左向きの加速度なのでマイナスを加える)。そのため、以下のように角振動数ωを計算できます。
\(-\displaystyle\frac{mgx}{l}=m(-ω^2x)\)
\(\displaystyle\frac{g}{l}=ω^2\)
\(ω=\sqrt{\displaystyle\frac{g}{l}}\) (\(ω>0\))
こうして、角振動数ωを得ることができます。また周期\(T\)については、以下のように計算しましょう。
\(ωT=2π\)
\(T=\displaystyle\frac{2π}{ω}\)
\(T=2π\sqrt{\displaystyle\frac{l}{g}}\)
単振り子の計算では、近似(単振動とみなす)によって計算できます。
単振動での公式の作り方を学び、運動方程式の立て方を理解する
力学で難しい内容の一つに単振動があります。なぜ単振動が難しいかというと、公式を覚えても意味がないからです。応用問題が出されると、公式を利用できません。そこで単振動では公式を覚えず、公式を作れるようにしましょう。
単振動の計算をするとき、出発点によってsinθを使うのか、それともcosθを使うのかが異なります。またベクトル(運動の向き)によっても、符号がプラスなのかマイナスなのかが変わります。この違いを見極めましょう。
なお単振動で公式を覚える必要はないものの、角振動数や周期を得るときに必要なので、\(a=-ω^2x\)は例外的に覚えましょう。この公式は振り子の単振動(単振り子)の計算をするときにも利用されます。
単振動では公式が役に立たないからこそ、公式の意味や式の作り方を理解しましょう。そうして運動方程式の作ることで計算できるようになるといいです。