加速度の概念を学んだあと、私たちが理解しなければいけない内容が重力です。すべての物体には重力がかかっており、常に下向きに加速度がかかっています。
物体を落とすと、最初はスピードが遅いものの、徐々に加速していきます。これは、重力として加速度がかかっているからです。
力学を学ぶとき、重力が関わる最も基本的な内容に自由落下、鉛直投げ下げ、鉛直投げ上げがあります。等加速度直線運動の公式を利用することによって、これらの問題を解くことができます。つまり、新たに公式を覚える必要はありません。
それでは物体を落としたり、上に投げたりするとき、物体はどのような動きをするのでしょうか。加速度として重力を利用するときの運動を確認しましょう。
もくじ
すべての物体には下向きに重量\(g\)が加わる
既に知っている通り、すべての物体には重力が加わっています。すべての物体は地球によって下向きに引っ張られているのです。つまり、常に下向きに加速度が加わっています。下向きの加速度(重力)があるため、物体は落下するのです。
また重力は加速度に関わっているため、時間経過と共に落下スピードが速くなります。このときの加速度を重力加速度と呼び、重力加速度は\(g\)と表すことができます。
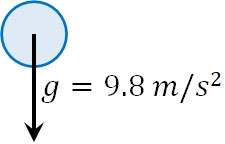
また重力加速度は値が決まっており、9.8m/s2です。重力が関わる物理の問題が出されるとき、必ず重力加速度は9.8m/s2になることを覚えておきましょう。
自由落下・鉛直投げ下げ・鉛直投げ上げの概要
なお重力加速度を学ぶとき、最初に理解しなければいけない内容が以下の3つです。
- 自由落下
- 鉛直投げ下げ
- 鉛直投げ上げ
自由落下では、静止している状態から物体を落とします。当然、加速度\(g\)にて、物体は地面に向かって速度を上げながら落ちていきます。また鉛直投げ下げでは、地面に向かって物体を投げます。そのため、地面に向かって速度が付いている状態から、さらに時間経過と共に重力加速度が加わります。
一方で鉛直投げ上げでは、上に向かって物体を投げます。そのため、どこかの時点で物体は落ちてきます。

重要なのは、重力加速度の符号です。重力加速度は必ず下向きに働きます。そのため、符号がプラスになることがあれば、マイナスになることもあるのです。
自由落下と鉛直投げ下げでは、物体は地面に向かって落ちていきます。この方向は重力加速度の向きと同じなので、加速度は\(g\)です(符号はプラス)。
それに対して鉛直投げ上げでは、物体は最初、上に向かって動いています。ただ重力加速度の向きは反対です。そのため、加速度は\(-g\)です(符号はマイナス)。加速度がマイナスなので、鉛直投げ上げでは物体の速度が徐々に遅くなり、ある時点から物体は落下します。
・等加速度直線運動の公式を利用する
なお自由落下、鉛直投げ下げ、鉛直投げ上げで利用する公式は共通しています。等加速度直線運動で利用される以下の公式を使いましょう。
- \(v=v_0+at\)
- \(x=v_0t+\displaystyle\frac{1}{2}at^2\)
- \(v^2-v_0^2=2ax\)
教科書によっては、自由落下や鉛直投げ下げ、鉛直投げ上げに関する公式をそれぞれ記載していることがあります。ただ公式を暗記しても意味がないですし、力学の理解を複雑にするだけなので絶対に覚えないようにしましょう。利用する公式は等加速度直線運動で利用される3つの公式だけで問題ありません。
自由落下では初速度\(v_0\)が0になる
それでは、自由落下を確認していきましょう。自由落下では、静止している状態から物体を落とします。つまり、自由落下では必ず初速度\(v_0\)が0になります。
初速度が0であり、加速度は9.8m/s2と一定であるため、経過時間がわかれば速度の計算が可能です。例えば物体を自由落下させるとき、5秒後の速さは49m/sです。
\(v=9.8×5=49\)
また、物体は5秒後に122.5m下に落下しています。
\(x=\displaystyle\frac{1}{2}×9.8×5^2=122.5\)
\(v_0=0\)にて、公式に値を代入すれば答えを得ることができます。先ほど、等加速度直線運動の公式を記しました。
- \(v=v_0+at\)
- \(x=v_0t+\displaystyle\frac{1}{2}at^2\)
- \(v^2-v_0^2=2ax\)
この公式に対して、\(v_0=0\)を代入すると自由落下で利用できる公式になります。
鉛直投げ下げでは初速度\(v_0\)が存在する
それでは、鉛直投げ下げではどうなるのでしょうか。静止状態から物体を落とす自由落下とは異なり、勢いをつけて物体を下に投げ、落下させるのが鉛直投げ下げです。そのため自由落下とは異なり、初速度\(v_0\)があります。
つまり自由落下に対して、初速度\(v_0\)を加えると鉛直投げ下げになります。
先ほど、自由落下では初速度を\(v_0=0\)にして考えました。それに対して、鉛直投げ下げでは以下の等加速度直線運動の公式を利用して計算しましょう。
- \(v=v_0+at\)
- \(x=v_0t+\displaystyle\frac{1}{2}at^2\)
- \(v^2-v_0^2=2ax\)
鉛直投げ下げでは、速度の向きと重力加速度の向きが同じです。そのため、等加速度直線運動の公式を利用できます。
自由落下と鉛直投げ下げでの練習問題
それでは、実際に問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 物体Aをビルの屋上から自由落下させたあと、2秒後に物体Bを投げおろしました。さらにその2秒後に物体Aと物体Bが同時に地面に到着しました。なお重力加速度を\(g\)とします。
- ビルの高さはいくらですか
- 物体Bの投げおろしたときの初速度はいくらですか。
1) ビルの高さはいくらですか
物体Aを自由落下させ、合計で4秒後に地面に到着しています。そこで以下のように計算しましょう。
\(x=v_0t+\displaystyle\frac{1}{2}at^2\)
\(x=0+\displaystyle\frac{1}{2}g×4^2\)
\(x=8g\)
こうして、ビルの高さは8g mとわかります。なお正確な高さを計算したい場合、\(g=9.8\)を代入して計算すればいいです。
2) 物体Bの投げおろしたときの初速度はいくらですか
ビルの高さは既に計算しています。そこでビルの高さを利用して、物体Bの初速度を計算しましょう。また物体Bは投げおろして2秒後に地面に到着しているため、\(t=2\)です。
\(x=v_0t+\displaystyle\frac{1}{2}at^2\)
\(8g=2v_0+\displaystyle\frac{1}{2}g×2^2\)
\(2v_0=6g\)
\(v_0=3g\)
こうして、物体Bの初速度は3g m/sとわかりました。
鉛直投げ上げでは逆方向に加速度(重力)が加わる
次に鉛直投げ上げを学びましょう。鉛直投げ上げで重要なのは、速さの向きと重力加速度の向きが逆であることです。鉛直上向きに物体を投げ上げる場合、速さの向きとは逆向きに加速度が加わるのです。

鉛直投げ上げでは、時間経過と共にスピードが遅くなります。また、ある時点から落下します。この理由は、逆向きに加速度が加わっているからです。
速度と逆向きに加速度が加わっているため、鉛直投げ上げの加速度は\(g\)ではなく、\(-g\)となります。加速度がプラスだと、時間経過と共に速度が速くなります。ただ、それでは自然現象と合致しません。そこで日常的に経験している現象と同じにするため、加速度を\(-g\)にしましょう。
なお前述の通り、利用する公式は以下の3つです。
- \(v=v_0+at\)
- \(x=v_0t+\displaystyle\frac{1}{2}at^2\)
- \(v^2-v_0^2=2ax\)
等加速度直線運動では、利用する公式はすべて同じです。ただ加速度は\(g\)ではなく\(-g\)です。そのため鉛直投げ上げでは、\(g\)を\(-g\)に変えて計算しましょう。
最高点への到達では速度が0になる
なお力学の問題で鉛直投げ上げが出題されるとき、最高点への到達時間や距離を問われます。鉛直投げ上げで最高点に到達する場合、どのように計算すればいいのでしょうか。
物理の問題を解くとき、物体がスローモーションで動いている場面を想像しましょう。最高点に到達する場面では、物体の速度は徐々に遅くなり、最終的に速度は0になります。
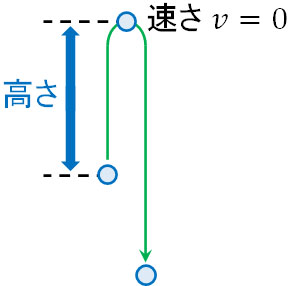
また速度が0になった瞬間というのは、物体が最高点に達していることを意味します。つまり最高点の到達時間やスタート地点から最高点までの距離(高さ)を計算したい場合、物体の速度を0にして計算すればいいとわかります。一瞬だけ速度が0になっている場面を想像すれば、最高点の到達時間やスタート地点から最高点までの高さを計算できます。
鉛直投げ上げでの練習問題
それでは、鉛直投げ上げに関する問題を解きましょう。以下の問題の答えは何でしょうか。
- 物体を鉛直上向きに速度\(v’\) m/sで投げ上げました。重力加速度を\(g\)とします。
- 最高点に到達する時間と最高点の高さ(スタート地点から最高点までの距離)を求めましょう。
- 物体がスタート地点に戻ってくるときの時間を求めましょう。
- 物体がスタート地点に戻ってくるときの速さを求めましょう。
1) 最高点に到達する時間と最高点の高さを求めましょう
まず、最高点に到達する時間を計算しましょう。前述の通り、最高点では速さ\(v\)が0です。そのため、以下のようになります。
\(v=v_0+at\)
\(0=v’-gt\)
\(t=\displaystyle\frac{v’}{g}\)
こうして、最高点の到達時間は\(\displaystyle\frac{v’}{g}\)秒であるとわかります。また最高点への到達時間が判明したため、最高点の高さも計算できます。
\(x=v_0t+\displaystyle\frac{1}{2}at^2\)
\(x=v’×\displaystyle\frac{v’}{g}-\displaystyle\frac{1}{2}g×\displaystyle\frac{v’^2}{g^2}\)
\(x=\displaystyle\frac{v’^2}{g}-\displaystyle\frac{v’^2}{2g}\)
\(x=\displaystyle\frac{v’^2}{2g}\)
こうして、高さは\(\displaystyle\frac{v’^2}{2g}\) mとわかります。
2) 物体がスタート地点に戻ってくるときの時間と速さを求めましょう
物体がスタート地点に戻るというのは、高さ(距離)が0であることを意味します。そこで距離に0を代入して計算しましょう。
\(x=v_0t+\displaystyle\frac{1}{2}at^2\)
\(0=v’t-\displaystyle\frac{1}{2}gt^2\)
\(0=t\left(v’-\displaystyle\frac{gt}{2}\right)\)
つまり\(t=0\)、または\(v’-\displaystyle\frac{gt}{2}=0\)のとき、距離(高さ)は0です。\(v’-\displaystyle\frac{gt}{2}=0\)になるためには以下のように計算します。
\(v’-\displaystyle\frac{gt}{2}=0\)
\(\displaystyle\frac{gt}{2}=v’\)
\(t=\displaystyle\frac{2v’}{g}\)
なお\(t=0\)はスタート地点を指します。そのため物体を投げた後、戻ってくるまでの時間は\(\displaystyle\frac{2v’}{g}\)秒です。
参考までに、計算しなくても戻ってくる時間を得ることが可能です。「物体を上に投げて最高点に到達する時間」と「物体が最高点に到達した後、スタート地点に戻ってくる時間」は同じです。そのため、最高点の到達時間は先ほど計算して得られた答えである\(\displaystyle\frac{v’}{g}\)を2倍すればいいとわかります。
3) 物体がスタート地点に戻ってくるときの速さを求めましょう
物体の初速度は\(v’\) m/sであるため、スタート地点に戻ってくるときの速度は計算しなくても\(-v’\) m/sとわかります。計算したい場合、以下のように公式を利用して計算しましょう。
\(v^2-v_0^2=2ax\)
\(v^2-v’^2=-2g×0\)
\(v^2=v’^2\)
\(v=v’,-v’\)
こうして、計算によっても速度は\(-v’\) m/sになるとわかりました。
公式を利用し、物体が落下するときの運動を理解する
物体が落下するときは自由落下、鉛直投げ下げ、鉛直投げ上げの3種類があります。どれも考え方は同じであり、利用する公式も同じです。
ただ、重力加速度の向きに注意しましょう。自由落下と鉛直投げ下げでは、速度と重力加速度の向きが同じです。それに対して鉛直投げ上げでは、速度と重力加速度の向きが逆です。そのため、鉛直投げ上げでは\(-g\)を利用して計算しましょう。
なお物理の問題を解くとき、実際に物体が動いている場面を頭の中で想像しましょう。そうすれば、重力加速度の向きがわかり、最高点に到達するときの時間を計算できるようになります。
高校物理で最も基本的な内容の一つが落体運動の計算です。重力加速度と公式を利用し、計算問題を解けるようにしましょう。






