物理や化学で気体の計算問題を解くとき、気体の状態方程式がひんぱんに利用されます。ただ気体の状態方程式を利用するには条件があり、理想気体でなければいけません。
ただ現実世界で理想気体は存在しません。必ず実在気体となります。そこで理想気体と実在気体の違いを理解しましょう。また、どのような条件であれば実在気体が理想気体に近づくのかについても理解しましょう。
実在気体には分子間力と分子の体積が存在します。そのため、実在気体では気体の状態方程式を利用することができません。
物理や化学で理想気体と実在気体の違いを学ぶのは重要です。そこで、実在気体の特徴や性質を解説していきます。
もくじ
状態方程式で利用される理想気体
物理や化学で気体の計算をするとき、すべての人が気体の状態方程式を利用します。以下が気体の状態方程式です。
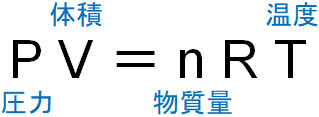
ただ気体の状態方程式を利用するためには、理想気体でなければいけません。理想気体というのは、分子間力や分子の体積が存在しない気体を指します。
すべての物質には、互いに引き合う力が存在します。これが分子間力であり、分子同士で引力を生じるのです。また分子には小さいながらも体積があります。分子の体積とは、分子の大きさと考えましょう。このとき理想気体では、分子に大きさがありません。
つまり気体の状態方程式というのは、分子同士の引力が存在せず、分子に大きさがないという特殊な状態を想定しています。
実在気体には分子間力や分子の体積が存在する
ただ当然ながら、実際には分子に分子間力が働きますし、分子の体積もあります。そのため実際の気体というのは、理想気体とは性質が異なります。
理想気体と実在気体では以下の違いがあります。
| 理想気体 | 実在気体 | |
| 分子間力 | なし | ある |
| 分子の体積 | なし | ある |
| PV=nRT | 成立する | 成立しない |
圧力が低く、温度が高い状態の場合、実在気体は理想気体の状態に近づきます。一方で圧力が高かったり、温度が低かったりする場合、分子間力や分子の体積による影響が大きくなります。そのため、実在気体と理想気体を区別しなければいけません。
理想気体と実在気体でのグラフ
それでは、理想気体と実在気体でどのようにグラフが異なるのか確認しましょう。まず、物質量が1molの気体を考えます。この場合、気体の状態方程式を利用すると以下のように表すことができます。
\(PV=1×RT\)
\(\displaystyle\frac{PV}{RT}=1\)
理想気体の場合、常に\(\displaystyle\frac{PV}{RT}=1\)となります。一方、実在気体では圧力や温度の影響により、\(\displaystyle\frac{PV}{RT}=1\)からズレるようになります。例えば温度を一定(27℃)にする場合、横軸を圧力P、たて軸を\(\displaystyle\frac{PV}{RT}\)とすると、グラフは以下のようになります。
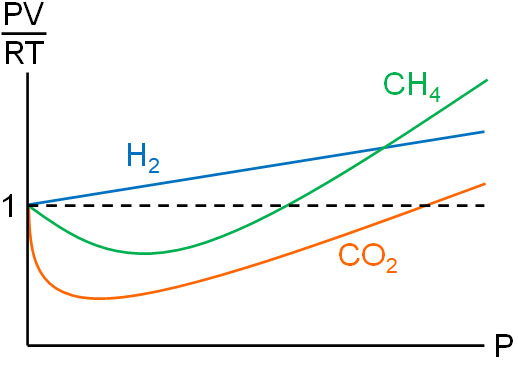
このように、条件によって\(\displaystyle\frac{PV}{RT}=1\)からのズレが大きくなります。
なおH2に比べて、CO2では分子量が大きいために分子間力による影響が大きく、分子の体積も大きいです。そのためH2は圧力による影響が少ない一方、CO2は環境による影響を強く受けます。
圧力の変化によってグラフの値が変化する理由
それでは、なぜ先ほど提示したグラフのように実在気体では\(\displaystyle\frac{PV}{RT}=1\)からずれるのでしょうか。まず、圧力が低い場面を考えてみましょう。
グラフを確認すると、圧力が低い状態では\(\displaystyle\frac{PV}{RT}<1\)となっています。なぜ\(\displaystyle\frac{PV}{RT}<1\)になるかというと、分子間力の影響によって分子は互いに引き合うからです。
温度と圧力が一定の場合、変化するのは容器の体積Vです(容器の体積を自由に変えることができる場合)。理想気体では分子間力がないため、PV(圧力と容器の体積のかけ算)は一定です。一方で分子間力がある場合、引力によって分子同士が互いに引き合い、容器の体積が小さくなります。これが、低圧力の環境下で\(\displaystyle\frac{PV}{RT}<1\)となる理由です。
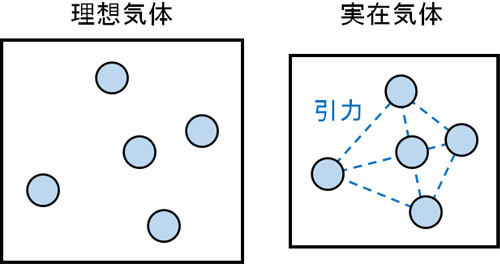
グラフで\(\displaystyle\frac{PV}{RT}=1\)よりも低い部分というのは、分子間力が影響していると理解しましょう。
一方、圧力が非常に高い環境ではどうでしょうか。\(\displaystyle\frac{PV}{RT}>1\)というのは、理想気体よりも容器の体積Vが大きいことを意味しています。前述の通り圧力と温度が一定の場合、変化するのは容器の体積だけです。
理想気体の場合、分子の体積(分子の大きさ)が存在しません。そのため圧力を加えると、無限に小さくなります。それに対して実在気体では、分子には大きさがあります。分子の大きさよりも小さくなることは物理的にできないため、圧力が大きいと理想気体に比べて容器の体積が大きくなります。
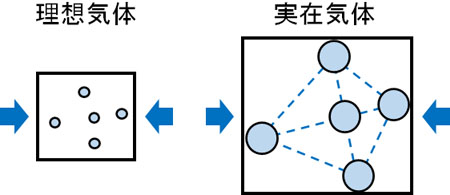
つまりグラフで\(\displaystyle\frac{PV}{RT}=1\)よりも高い部分というのは、分子の体積が影響しています。分子の大きさは小さいものの、圧力が非常に大きい場合、分子の体積が容器の体積へ影響するようになります。その結果、理想気体よりも容積の体積が大きくなり、\(\displaystyle\frac{PV}{RT}>1\)となります。
分子間力や温度の違いによる理想気体と実在気体
それでは、なぜCH4はCO2よりも下へ行く度合いが小さいのでしょうか。この理由について、CO2よりもCH4のほうが分子量が小さいからです。分子が小さいため、分子間力(ファンデルワールス力)による引力が弱いのです。
CH4は分子間力が小さく、CO2よりも分子同士の引力が弱いため、圧力が低い環境ではCO2よりも理想気体からのズレが小さいです。
なお分子間力が重要であるため、例えば水素結合による強い引力が働くアンモニア(NH3)では、二酸化炭素(CO2)よりもグラフで大きく下に下がります。CH4とCO2は両方とも無極性分子です。一方でNH3は強い極性をもつため、分子間力が強く、理想気体とのズレが大きくなるのです。
理想気体に近づくための条件:圧力と温度
それでは、理想気体に近づくための条件には何があるのでしょうか。一つは「圧力が低い」ことです。
気体の状態方程式では、PVは常に一定です。圧力が低いというのは、容器の体積が非常に大きいことを意味しています。つまり圧力が低い場合、分子は容器中に幅広く拡散します。そのため分子同士が近づく機会が少なく、分子の引力による影響が少ないです。
また容器の体積が大きい場合、分子同士の大きさによる影響も少なくなります。これが、低圧力の環境で実在気体が理想気体に近づく理由です。
・温度が高いと理想気体に近づく
ここまで、圧力に焦点を当てて解説してきました。もう一つ、実在気体が理想気体に近づく条件として温度があります。温度が高い場合、実在気体は理想気体に近づきます。
例えばメタン(CH4)について、温度が200Kの場合と400Kの場合を比較すると以下のようになります。
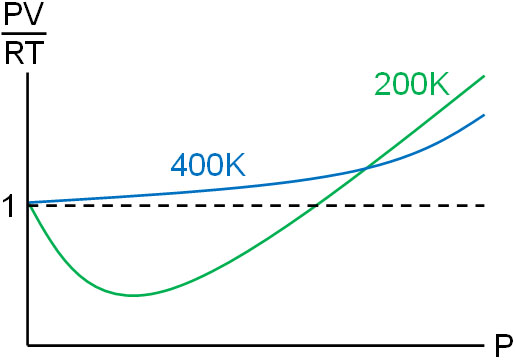
温度が高い状態では、分子による動きが激しいです。この場合は分子同士の引力による影響は少なくなります。
前述の通り、\(\displaystyle\frac{PV}{RT}=1\)よりも低い部分は分子間力が関与しています。そのため温度が高く、分子間力による影響を無視できる場合、理想気体に近づきます。
つまり実在気体が理想気体に近づくためには、圧力が低く、温度が高ければいいとわかります。
理想気体と実在気体の性質を理解する
気体の計算では状態方程式をひんぱんに利用するものの、このときは理想気体であるという前提条件があります。そこで、理想気体とは何かを理解しましょう。
実際のところ、理想気体は存在しません。理想気体では、分子間力と分子の体積が存在しないからです。ただ、現実世界に存在するのは実在気体です。そのため分子間力と分子の体積による影響により、\(\displaystyle\frac{PV}{RT}=1\)から値がずれます。
そこで、圧力や温度の変化によってどのように\(\displaystyle\frac{PV}{RT}=1\)から値がズレるのか理解しましょう。また、どのような条件のときに実在気体が理想気体に近づくのかも学びましょう。
物理や化学で学ぶのが理想気体と実在気体です。両者の関係は重要であり、分子間力と分子の体積による影響によってどのように値が変化するのか把握しましょう。






