すべての実験では有効数字が非常に重要になります。物理や化学、生物とあらゆる場面で有効数字が関わってきます。
特に化学を学ぶ場合、必ず有効数字を意識しなければいけません。実際には化学以外にも物理や生物で実験をするとき、有効数字を利用するものの、学問として学ぶときは化学で特に有効数字が利用されるというわけです。
それでは、有効数字はなぜ重要なのでしょうか。また、どのように有効数字を利用して計算すればいいのでしょうか。
有効数字を利用するとき、足し算・引き算とかけ算・割り算で計算方法が違います。ただ、ルールを覚えれば有効数字の計算は簡単です。そこで、どのように有効数字を利用して計算すればいいのか解説していきます。
もくじ
どれだけ信用できるのかが有効数字で重要
数学で計算をするとき、勝手に数字を変えてはいけません。すべての数字に意味があるため、数学に有効数字という概念は存在しません。
一方で科学実験をする場合、有効数字の概念が非常に重要になります。特に学問として化学を学ぶとき、有効数字がひんぱんに活用されます。有効数字とは、「どれだけその値を信用できるのか」を表します。
例えば、あなたの家から近くの病院までの距離は何kmでしょうか。このとき、多くの人は「恐らく5kmと思う」のように答えると思います。つまり5kmかもしれないし、実際には6kmの距離かもしれません。
一方、正確に距離を測って「あなたの家から近くの病院までの距離は5.00km」とわかったとします。どちらも、値としては5kmです。ただ正確に測定して5.00kmとわかった場合、家から病院までの距離はピッタリ5kmです。
数字があいまいな場合、値の変動幅が大きいです。有効数字を学ぶとき、この概念を知ることが重要になります。
実際の実験では、最も低い位は信用性が低い
それでは、なぜ数字のあいまいさを知ることが重要なのでしょうか。学問で物理や化学、生物を学ぶとき、問題を解くにしても、数字が与えられて計算することになります。
ただ現実世界では、実験をすることになります。大学の研究室であれば、研究データを集めます。工場であれば、不良品が混ざっていないか確認します。医療であれば、患者さんの血液データを読み解くことになります。

このように、実際にデータを測定することによって結果を得られます。こうした結果を読み解くとき、誤差が生まれます
例えば酸と塩基を用いて中和滴定をするとき、目盛りの最後の位について、どの値を採用するのかはあなたの自由です。
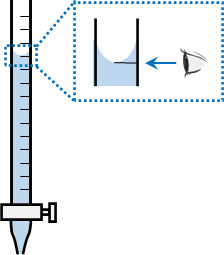
例えば、加えた溶液の量は5.5mLかもしれないし、5.6mLかもしれません。また人が違えば、5.4mLを加えたと考える人もいるかもしれません。つまり実験をするとき、最後の位は正確な値ではなく、誤差となるのです。
なお目視によって得た値ではなく、機器を用いて測定した場合であっても、最後の位は正確な値ではありません。温度や湿度、わずかな試薬の量の違いによって値が変動するからです。
なお実際のところ、まったく同じ条件で再び実験したとしても得られるデータ(結果)は変わります。大幅な値の変動はなくても、多少の値の変動はあるのです。実験をするときに毎回結果が変動するのは普通であり、特に最も低い位は信用性が薄いです。
科学実験でデータを得るときは、低い位の値は信用性が低いため、有効数字の概念が重要になります。
有効数字2ケタや3ケタの概念:0.2と0.20は異なる数字
このように理解すると、0.2と0.20は異なる数字であるとわかります。実験によって0.2という値を得る場合、測定する人が違えば0.4という結果になるかもしれません。また実験するときの温度が5℃高いと、0.1という結果になるかもしれません。
一方で0.20という値の場合、0.20の周辺に真の値があります。このとき、測定する環境によっては結果が0.22になるかもしれませんし、0.17になるかもしれません。つまり0.20というのは、0.16~0.24の範囲に収まります。
ひとまず物理や化学、生物での実験では、最も低い位は信頼性が低いという事実を理解しましょう。
・有効数字の数え方
それでは、実際に有効数字を利用して数えてみましょう。ひんぱんに利用されるのは有効数字2ケタと有効数字3ケタです。有効数字2ケタとは、以下のように2つの数字が並んでいる状態を指します。
- 12
- 3.2
- 4.0
一方で有効数字3ケタでは、以下のように3つの数字が並びます。
- 847
- 23.1
- 7.90
数字がいくつあるのかを数えることによって、有効数字の数がわかります。
最初に0をもつ数字の場合、0以外の数字が出たら有効数字をカウントする
注意点として、最初に0をもつ数字については、0以外の数字が表れたところから有効数字をカウントしましょう。例えば、以下はすべて有効数字2ケタです。
- 0.53
- 0.085
- 0.0030
- 0.00074
左側に存在する0を省く場合、すべてのケースで2つの数字が並びます。この場合、有効数字は2ケタです。
それに対して、以下は有効数字3ケタです。
- 0.847
- 0.0480
- 0.00700
- 0.000142
先ほどと同様に左側にある0をすべて省く場合、3つの数字が並びます。この場合、有効数字は3ケタです。
左側にある0を無視する理由としては、単位によって値が大きく変化するからです。例えば、1cmは0.01mです。また、1gは0.001kgです。そのため有効数字を数えるとき、左側にある0を省かなければいけません。
・10の累乗を利用して表記することは多い
なお値が小さい場合、10の累乗を利用して表記することがひんぱんにあります。例えば、0.00000030と表記してもいいですが、どのような数字なのか理解しにくいです。そこで、以下のように表記します。
- 3.0×10-7
この場合、有効数字2ケタで0.00000030を表しています。
足し算・引き算での有効数字は最も低い位に着目する
それでは、有効数字を利用して計算するにはどうすればいいのでしょうか。まず、足し算と引き算について確認しましょう。足し算と引き算では、同じ考え方によって計算することができます。
足し算や引き算をするとき、「右端の位に着目し、最も位の高い数字に合わせる」というルールがあります。
恐らく意味を理解できないと思うので、実際に計算してみましょう。まず、以下のように数字の右端に着目します。
- 5.31
- 32.4
- 0.0384
例えば、以下の計算の答えは数学だと37.6716です。
\(5.31+32.4-0.0384=37.6716\)
ただ科学実験をする場合、有効数字を利用します。先ほどの計算をするとき、右端の位に着目すると以下のようになります。
- 5.31:右端の位は100分の1
- 32.4:右端の位は10分の1
- 0.0384:右端の位は10000分の1
これらの数字のうち、「右端が最も高い位をもつ数字」に有効数字を合わせましょう。先ほどのケースであれば、32.4は右端の位が10分の1です。つまり、5.31(右端の位は100分の1)や0.0384(右端の位は10000分の1)に比べて、右端の位が高いです。
そこで、右端の位を10分の1にそろえましょう。つまり37.6716について、100分の1の位を四捨五入し、10分の1の位をもつ数字に変えるのです。
\(37.6716≒37.7\)
こうして、化学実験では37.7を利用します。
・足し算や引き算での有効数字のルール
なぜ、このようなルールになっているのでしょうか。それは、前述の通り右端の位は不正確な数字だからです。例えば、以下の計算をしましょう。
- \(32.4+5.31=37.71\)
このとき32.4というのは、実験するときの条件(温度や湿度、試薬濃度のわずかな違いなど)が変わることによって、次の日に再び実験すると32.2というデータを得られるかもしれません。仮にデータが32.4から32.2に変わる場合、結果は以下のようになります。
- \(32.2+5.31=37.51\)
こうして、結果は37.71から37.51へ変わります。このように考えると、先ほどの結果(37.71と37.51)について、100分の1の位(37.51の1)は意味がないとわかります。
100分の1の位を足したり引いたりしても、10分の1の位が不正確であるため、当然ながら100分の1の位は不正確になります。そこで足し算や引き算をするとき、それぞれの数字について右端の位に着目した後、最も位の高い数字に合わせる必要があるのです。
かけ算・割り算では有効数字のケタ数に着目する
一方でかけ算と割り算ではどのように計算すればいいのでしょうか。まず、割り算はかけ算に直すことができます。そのため、かけ算での有効数字のルールを理解すれば、同じルールを割り算にも適用することができます。
かけ算では、足し算や引き算とは異なるルールがあります。ただ、有効数字を利用するときのかけ算のルールは単純です。かけ算をするとき、最も低い有効数字(ケタ数)をもつ数字に答えを合わせましょう。
例えば数学では、以下の計算式の答えは3.59168です。
\(2.3×0.122×12.80=3.59168\)
ただ科学実験では、有効数字を考慮しなければいけません。先ほどの計算式について、それぞれの数字の有効数字は以下のようになります。
- 2.3:有効数字2ケタ
- 0.122:有効数字3ケタ
- 12.80:有効数字4ケタ
このときかけ算や割り算では、前述の通り最も低い有効数字(ケタ数)をもつ数字に答えを合わせます。これらの数字の中でも、最も低い有効数字は2ケタです。そこで、有効数字を2ケタにしましょう。つまり、3.59168を3.6に変える必要があります。
・かけ算や割り算での有効数字のルール
それではかけ算(または割り算)をするとき、なぜ最も低い有効数字に合わせる必要があるのでしょうか。これは、かけ算をすると多くの位で不正確な答えとなるからです。
例えば、\(0.122×2.3\)の計算をする場面を考えてみましょう。この場合、四角で囲っている数字は不正確な数字です。
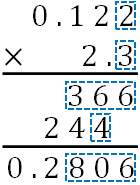
不正確な数字を利用してかけ算や割り算をする場合、答えの値は不正確です。またこのように確認すると、複数の位で不正確な数字が含まれているとわかります。
計算過程を確認すると、0.122(有効数字3ケタ)と2.3(有効数字2ケタ)をかけるとき、なぜ答えが0.28(有効数字2ケタ)で表記するべきなのかわかります。
有効数字を3桁とする場合、答えは0.281となります。ただ0.281のうち、8と1の数字は不正確です。8よりも低い位を含める意味はありません。そこで有効数字2ケタにすることで、0.28とします。有効数字のケタ数が低い数字に合わせるのはこうした理由があるのです。
有効数字が指定されていない場合の計算方法
それでは、有効数字が指定されていない場合はどのように計算すればいいのでしょうか。「有効数字2ケタとする」「有効数字3ケタとする」などのように、問題文に有効数字が指定されている場合、答えを出すのは容易です。
一方、有効数字が問題文で指定されていないケースもあります。また科学実験をする場合、どの有効数字を採用すればいいのかあなたが考えなければいけません。
この場合、計算で利用する数字に着目して、答えで利用する有効数字を決定しましょう。例えば、以下の計算問題があるとします。
- 1.2mol/Lの塩酸水溶液を316mL取り、ビーカーへ移します。ビーカーに存在する塩酸の物質量はいくらでしょうか。
計算すると以下のようになります。
\(1.2×\displaystyle\frac{316}{1000}=0.3792\)
ただあなたが塩酸を316mL取るとき、実際には315mLの塩酸水溶液しかビーカーへ移せていないかもしれません。場合によっては、317mLの塩酸水溶液をビーカーに移しているかもしれません。そのため、ビーカーの中に0.3792molがピッタリ存在することはありません。
そこで有効数字を利用しましょう。先ほどの計算で利用したのは1.2mol/L(有効数字2ケタ)と316mL(有効数字3ケタ)です。そこで答えでは有効数字2ケタを採用し、0.38molが正解になります。
問題文で有効数字を指定されていなかったとしても、計算で利用する数字から、有効数字を決定できるようになりましょう。
実験で重要な有効数字の概念
物理や化学、生物を含め、すべての実験操作で有効数字が利用されます。私たちが実験をするとき、データには必ず不正確な値が含まれます。そのため、有効数字を利用しましょう。
特に化学では有効数字がひんぱんに利用されます。足し算や引き算、かけ算、割り算をするとき、どのように有効数字を利用すればいいのか理解しましょう。ルールを覚えれば、有効数字を用いた計算は難しくありません。
なお、問題文で有効数字を指定されていなくても、答えを出すときは計算に使われる有効数字を利用するのが一般的です。計算に利用する数字に着目し、有効数字を利用して答えを出しましょう。
化学を学ぶとき、新たな概念の一つが有効数字です。すべての実験操作で有効数字を考慮する必要があるため、有効数字の概念を理解するのは重要です。