実際に統計処理をするとき、多くの人が推測統計を利用します。少数のサンプルを利用することによって、全体の確率を予想するのが推測統計学です。
当然ながら、全データを集めるのは大変です。また、全データを集めるのが不可能なケースも多いです。このときは推測統計学を利用し、全体の確率を推測しなければいけません。そこで母集団や標本、母平均、標本平均の意味を理解しましょう。
また統計学では分散や標準偏差を利用します。全データを取り扱うときとは異なり、推定統計では特殊な方法によって分散を出します。これを不偏分散といいます。
推定統計学を学ぶとき、覚えなければいけない新たな概念がいくつもあります。そこで、それぞれの内容を解説していきます。
もくじ
推定統計学では正規分布すると仮定して計算する
統計学で最初に学ぶのが記述統計です。全データを解析することによって、確率を計算するのが記述統計になります。
当然ながら、全データを集めると統計の内容は正確です。そのため記述統計は優れています。ただ、現実的に記述統計が難しいケースは多いです。例えば大統領の支持率を調べるとき、国民全員に聞くのは時間とコストがかかります。そこで、1000~2000人ほどにアンケートを取って支持率を出します。
また製品を販売前、すべての製品に対して耐久試験を実施するわけにはいきません。全商品に耐久性試験をする場合、耐久性試験後の半壊した製品ばかりが出荷されることになります。そのため、ランダムに抽出した一部の製品のみ品質をチェックします。
このように、一部のデータを利用することによって全体の確率を推定することが頻繁にあります。これを推定統計といいます。
推定統計学では、一部のデータについて「正規分布する」と仮定します。必ず正規分布になるかどうかは不明であるものの、通常は正規分布になるため、データが正規分布になると仮定して確率を計算するのです。
母集団と標本の意味
推定統計学を学ぶとき、必ず出てくる単語が母集団と標本です。それでは、母集団や標本とは何なのでしょうか。
全データのことを母集団と考えましょう。例えば製品を作るとき、全製品が母集団です。一方、母集団の中から10個の製品を取り出し、品質チェックをするとします。このとき取り出した10個の製品を標本といいます。
母集団は非常に大きいサンプル数であるため、すべてのデータ(製品)を調べるのは現実的ではありません。そこでサンプルとして数個のデータを取得し、標本として利用するのです。標本というのは、母集団の一部と理解しましょう。
母分布の予想:標本平均で母平均を推定する
標本を利用することによって、元データの分布(母分布)の予想をします。母集団が正規分布すると仮定すれば、標本を利用することで母分布を推定できるのです。
そこで、標本の平均値(期待値)を計算してみましょう。例えば母集団の中から製品を10個ランダムに取り出し、重さを調べると平均1kgになったとします。この場合、「母集団についても製品の重さの平均は1kgである」と推定することができます。
つまり、「標本の平均値(期待値)=母平均(母集団の平均)」とみなします。
母平均を調べることはできません。例えば政権の支持率を調べるとき、国民全員のアンケートを取得するのは不可能です。アンケートに答えない人は多いからです。ただ標本を利用することにより、標本の平均値\(m\)と母平均が同じになると仮定すれば、母平均の推定が可能になります。
推測統計とは、要は「一部のデータを利用して、母分布の平均値や確率を計算する方法」と理解しましょう。例えば、以下の問題の答えは何でしょうか。
- 正方形ではない特殊な形をしたサイコロがあります。このサイコロを6回投げると、「4,4,4,6,6,3」という結果でした。一回のサイコロを投げるときの期待値はいくらでしょうか。
何百回もサイコロを投げることによって、期待値を計算することができます。ただ面倒なので、サイコロを6回投げることによって母平均を推測しましょう。標本について、平均値(期待値)を計算すると以下のようになります。
\(\displaystyle\frac{4+4+4+6+6+3}{6}=4.5\)
こうして、標本の期待値が4.5になるとわかりました。6つのデータを標本として利用し、平均値を計算しましたが、これを母平均とみなすことが可能です。いずれにしても、少ないデータを利用することで母集団の平均値を推測できるのです。
ランダムサンプリング:無作為抽出する重要性
このとき重要なのがデータ集めの方法です。ランダムサンプリング(無作為抽出)によって、ランダムにデータを取得しなければいけません。多くのメディアで情報が偏っているのは、ランダムサンプリングができていないからです。
例えば支持政党のデータを集めるとき、「電話を利用することによって昼に調査をする」という方法では、正しいデータを集めることができるでしょうか。この場合は無作為抽出をしているとはいえず、偏ったデータを得られます。
昼に電話をしてアンケートを取る場合、電話に出るのはどのような人でしょうか。少なくとも、昼間に忙しく働いている人は電話を無視します。つまりアンケートに答えてくれるのは昼に家で過ごしている人であり、具体的には専業主婦またはリタイア後の老人です。
当然、こうした人からアンケートを取得して支持政党を聞いても最適な結果を得ることはできません。こうして、本来とは異なる誤ったデータが標本として集められます。
集めた標本がダメな場合、当然ながら正しく母集団を予想することはできません。ダメな標本を利用し、推定された母平均や確率というのは使い物にならないデータなのです。標本集めで無作為抽出が重要といわれるのは、こうした理由があります。
母分散・母標準偏差の推定をする
それでは次に、母分散(母集団の分散)の推定をしてみましょう。先ほど、標本平均を利用することによって母平均の推定をしました。同じように標本分散を利用することによって、母分散の推定をしましょう。また母分散を推測できれば、母標準偏差(母集団の標準偏差)を予想できます。
統計学を学んでいる場合、分散の計算方法は既に理解しているはずです。平均(期待値)を基準にして、「それぞれのデータとの距離を二乗した後に足し、平均化した値」が分散です。例えばデータが「0, 6, -1, 3, 8, 2」のとき、平均値は3であり、以下のように分散を計算します。
\(\displaystyle\frac{(-3)^2+3^2+(-4)^2+5^2+(-1)^2}{6}=10\)
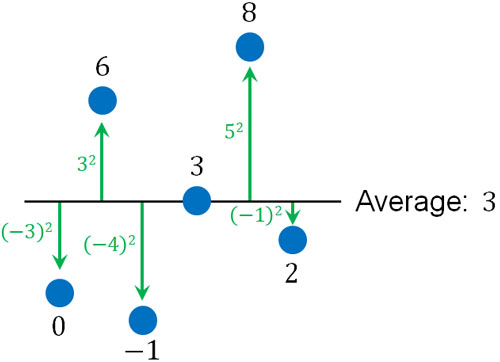
こうして、取得したデータについて分散を計算することにより、標本分散を求めることができます。
ランダムサンプリングにより、標本を信頼できる場合、標本分散と母分散とみなすことができます。こうして母分散の推定をします。
また母分散を予想できる場合、母標準偏差を計算できます。標本分散に平方根を加えることによって、標本標準偏差を得られます。このとき、標本標準偏差を母標準偏差とみなすのです。
不偏分散と不偏標準偏差を利用し、サンプル数を\(n-1\)にする
なお先ほど、標本分散を利用することによって母分散を推定する方法を解説しました。ただ実際の統計処理では、標本分散を利用することはありません。その代わりとして、サンプル数を\(n-1\)に変換して計算します。
先ほど分散を得るとき、以下のように「平均との差を二乗して足し、そのあとにサンプル数で割る」という作業をしました。
\(\displaystyle\frac{(-3)^2+3^2+(-4)^2+5^2+(-1)^2}{6}=10\)
6つの数字について平均との差を計算し、二乗したため、分散の計算をするときは6で割ります。ただ推測統計学では、分散を得るとき、サンプル数\(n\)に対して1を引いた数を利用します。つまり、以下のようになります。
\(\displaystyle\frac{(-3)^2+3^2+(-4)^2+5^2+(-1)^2}{\color{red}{5}}=12\)
このようにサンプル数である6ではなく、一つ小さい数である5を利用して割ります。このように、サンプル数から一つ小さい数を利用して計算する分散を不偏分散といいます。
平均(期待値)を\(μ\)、確率変数を\(X\)、サンプル数を\(n\)とすると、標本分散は以下の公式によって計算することができます。
- \(\displaystyle\sum_{k=1}^{n}{\displaystyle\frac{(X_k-μ)^2}{n}}\)
先ほどの計算を文字にすると、このような公式になります。一方で不偏分散の公式は以下のようになります。
- \(\displaystyle\sum_{k=1}^{n}{\displaystyle\frac{(X_k-μ)^2}{\color{red}{n-1}}}\)
母分布については、サンプル数が非常にたくさんあります。例えばサンプル数が1000の場合、1000で割っても、999で割っても答えに違いはほとんどありません。
一方で割る数が小さい場合、答えに大きな違いが表れます。例えば5で割るのと、4で割るのでは答えが大きく異なります。また重要なのは、「標本のように少ないサンプル数を用いて計算する場合、サンプル数\(n\)を利用するのではなく、\(n-1\)を利用するほうが実際の母分散に近い値を得られる」という事実がわかっていることです。
当然ながら、実際の値に近い計算方法を採用するほうが優れています。そのため推測統計学では、標本分散ではなく、不偏分散を利用するのが一般的です。
母分散に比べて、標本分散は値が小さくなる性質があります。そこで割る数を\(n-1\)にすることにより、割る数を小さい数に変換すれば、答えは少し大きい値が出ます。
なぜ\(n-1\)を利用するのかについて、理由を説明するのは難しいです。ただ経験的に不偏分散のほうが母分散に近い値が出るとわかっています。私たちは数学者ではないため、「不偏分散を利用すればいい」という事実を理解できれば問題ありません。
・不偏標準偏差を計算する
また不偏分散を得ることができれば、簡単に不偏標準偏差を計算できます。不偏分散に対して、平方根を加えましょう。これによって、不偏標準偏差を計算することができます。
標本分散よりも不偏分散のほうが母分散に近い値を得ることができるため、当然ながら標本標準偏差よりも、不偏標準偏差のほうが実際の母標準偏差に近い値を得ることができます。そのため推測統計では、ばらつきを計算するときに不偏標準偏差を利用します。
標本平均や不偏分散、不偏標準偏差を利用し、母分布を推測する
本来であれば、母集団を得ることによって確率の計算をするのが優れています。ただ記述統計として母集団を得られるケースは少なく、実際は一部のデータ(標本)を利用することによって確率の計算をします。
こうした推測統計では、標本平均を母平均とみなします。ランダムサンプリング(無作為抽出)が正しく行われている場合、標本平均を利用して母平均を推定するのです。
また母分散や母標準偏差の計算をするとき、標本分散や標本標準偏差を利用することは基本的にありません。そうではなく、不偏分散や不偏標準偏差を利用します。このほうが実際の母分散や母標準偏差に近い値を得られるからです。
一部のデータを利用して母分布の推定をするとき、これらの性質を理解しましょう。推測統計は多くの場面で利用されているため、正しくランダムサンプリングを行い、母集団の確率や平均(期待値)、分散、標準偏差を計算できるようにしましょう。






