等分散かどうかを確認する手法としてF検定が知られています。これにより、データの形を確認できます。
このとき統計学で最も利用される検定法にt検定があります。なぜF検定が重要かというと、スチューデントのt検定をするときにF検定を事前に行う必要があるからです。F検定を行い、等分散である(データの形が同じである)と確認されれば、スチューデントのt検定を利用できるというわけです。
またF検定をするためには、F分布を理解しなければいけません。F分布は分散の比を表します。またF分布を利用し、95%信頼区間よりも外れた値が出る場合、等分散ではないと判断できます。つまりF検定では、F分布を利用して判断します。
それでは、どのようにF検定をすればいいのでしょうか。また、どのように等分散かどうかを判断すればいいのでしょうか。ここでは、F検定の方法を解説していきます。
もくじ
F検定で分散が等しいかどうかを確認する
F検定によって何がわかるかというと、2つのデータを比べるとき、「同じデータの形をしているかどうか」をF検定によって判断できるのです。正規分布かどうかに関わらず、同じ形をしていれば等分散と判断します。
一方でグラフの形が異なる場合、たとえ2つのデータが正規分布していたとしても、不等分散とみなします。等分散かどうかというのは、以下のように判断しましょう。
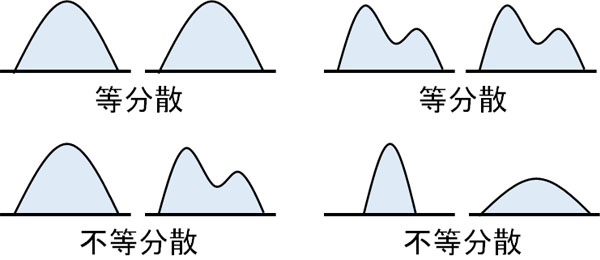
グラフの形が似ているかどうかを判定するのがF検定であるため、F検定の概念自体はそこまで難しくありません。
それでは、どのようにしてデータの形が同じかどうかを判断するのでしょうか。これには分散(または標準偏差)を利用します。データのばらつきを表すのが分散や標準偏差です。そのため2つのデータについて、ばらつきを比べたとき、分散の値が近いほどグラフの形が似ていると判断します。
そこで標本1の分散(不偏分散)を\((s_1)^2\)、標本2の分散(不偏分散)を\((s_2)^2\)とすると、統計量Fは以下の式によって表されます。
\(F=\displaystyle\frac{(s_1)^2}{(s_2)^2}\)
もちろん分散(標準偏差)が等しかったとしても、必ずしもグラフの形が同じとは限りません。ただ分散が同じ場合、高確率でデータの形が似ており、等分散であると判断することができます。
二標本t検定をする前、等分散・不等分散の確認でF検定が必要
それでは、なぜF検定が重要になるのでしょうか。この理由として、二標本t検定では等分散かどうかの確認が必要になるからです。
最も有名なt検定として、スチューデントのt検定が知られています。ゴセットという化学者によってt検定が発見されました。彼はスチューデントというペンネームで論文投稿したため、スチューデントのt検定と呼ばれています。
ただ、どのような場面であってもスチューデントのt検定が有効ではありません。スチューデントのt検定では、2つのデータが等分散である必要があります。t検定では「母集団が正規分布している」という前提があり、これに加えて標本のデータの形が似ていないといけないのです。
F検定を行い、2つのデータが不等分散であるとわかると、スチューデントのt検定をすることができません。そのためスチューデントのt検定をする場合、事前にF検定が必要というわけです。
ウェルチのt検定なら等分散の確認が不要
ただF検定を毎回するのは面倒です。そこで、ウェルチのt検定が開発されました。ウェルチのt検定を利用する場合、事前にF検定をする必要はありません。ウェルチのt検定では、等分散や不等分散に関係なくt検定をすることができるからです。
なお教科書通りには、以下の手順になります。
- F検定を行う
- 等分散の場合、スチューデントのt検定を行う
- 不等分散の場合、ウェルチのt検定を行う
ただ実際には、最初からウェルチのt検定をしても問題ありません。そのためF検定をしなくても、スチューデントのt検定を利用しなくても、ウェルチのt検定を利用して結論を述べていいのです。
ただすべての統計学の教科書にはF検定が記載されています。そこで統計の原理を理解するため、F検定を理解する必要があるのです。
F検定を学ぶため、F分布を理解する
そこでF検定を学ぶため、F分布について理解しましょう。F分布とは何かというと、分散の比と確率密度を表します。
データの形が異なる場合、分散の比は大きくなります。一方でデータの形が完全に同じ場合、分散の値(標準偏差の値)は同じになるため、分散の比は1になります。そこで横軸を分散の比、たて軸を確率密度で表すと以下のようになります。

どのようなグラフを描くのかについては、標本の自由度(サンプル数)によって異なります。いずれにしても、正規分布ではないグラフがF分布です。
なおF値を計算するとき、分散の値が大きいほうを分子にしましょう。
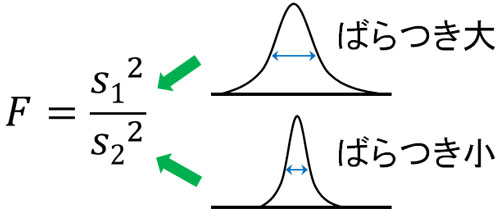
分子のほうが必ず数値が大きくなるため、F値を計算するときは必ず1よりも大きくなります。
なお分散の値の大きさを考慮しない場合、分母の値が分子の値よりも大きくなることがあります。この場合は両側検定によってF検定を行います。また、両側検定によってF検定を説明している教科書もあります。ただここでは、分子の値を必ず大きくすることによる片側検定で話を進めていきます。
F値は自由度\(n-1\)に従う
先ほど自由度によって、F分布のグラフが異なることを説明しました。つまり自由度によって、有意水準0.05となるF値も変わります。
このとき、F分布表での片側確率(\(P=0.05\))は以下のようになっています。

一部を記しましたが、このようなF分布表を利用することによって等分散かどうかを確認します。また、F値は自由度\(df_1=n_1-1\)、自由度\(df_2=n_2-1\)のF分布に従います。そのためF分布表を利用するとき、標本のサンプル数から1を引くようにしましょう。
例えば標本A(分子)のサンプルサイズ(データ数)が7であり、標本B(分母)のサンプルサイズ(データ数)が9の場合はどのようにF分布表(片側確率:\(P=0.05\))を利用すればいいのでしょうか。\(df_1=6\)、\(df_1=8\)であるため、以下の部分に着目しましょう。

こうして自由度が\(df_1=6\)、\(df_1=8\)のとき、F分布で有意水準が0.05となる部分が3.58になるとわかりました。
分散の比がF値となり、自由度によって有意水準\(P=0.05\)となる場所が異なる
それでは、このときのF値(3.58)は何を意味しているのでしょうか。先ほどのF分布表というのは、有意水準が0.05となるときのF値を意味しています。つまり\(df_1=6\)、\(df_1=8\)のとき、F値が3.58以上の面積は5%になります。
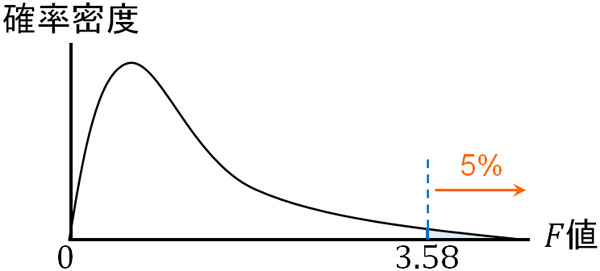
分母の値に対して、分子の値が大きく異なっている場合、分散の比の値(F値)も大きくなります。このときF値が3.58よりも大きい値であれば、「5%以下の確率で起こる稀なケースが起こっている」と判断できます。
分散の比がF値であり、F分布を利用することによって、どれくらいの確率で特定の事象が発生するのかを予測することができます。
例えば有意水準0.05となるF値よりも、標本Aと標本Bの分散比(F値)が大きい場合、等分散ではない(データの形が違っている)と結論付けることができます。
p値と帰無仮説・対立仮説を利用してF検定を行う
ここまでの内容を理解すれば、p値を計算することによってF検定をすることができます。それでは、実際にF検定をしてみましょう。例えば以下の標本Aと標本Bについて、等分散かどうかをF検定で調べてみましょう。
- 数学のテストを行い、AクラスとBクラスで以下の結果を得られました。2つの群は等分散でしょうか。
| Aクラス | Bクラス |
| 50 | 70 |
| 48 | 62 |
| 40 | 55 |
| 38 | 65 |
| 66 | 52 |
| 58 | 68 |
まず、帰無仮説と対立仮説を設定しましょう。
- 帰無仮説:分散に差はない(2つのデータは等分散)
- 対立仮説:分散に差がある(2つのデータは不等分散)
F分布を利用するとき、分散が重要になります。そこでそれぞれの標本について分散を計算しましょう。以下のようになります。
| Aクラス | Bクラス | |
| サンプル数\(n\) | 6 | 6 |
| 分散(不偏分散)\(s^2\) | 113.6 | 51.6 |
| 標準偏差(不偏標準偏差)\(s\) | 10.66 | 7.18 |
分散はAクラスのほうが大きいです。そこで分子を113.6、分母を51.6に設定してF値を計算しましょう。
\(F=\displaystyle\frac{113.6}{51.6}≒2.202\)
こうして、F値は2.202であるとわかりました。
次に、有意水準0.05となるF値を確認しましょう。それぞれの標本について、サンプル数は6です。そのため、F分布表で利用する自由度は両方とも5です。
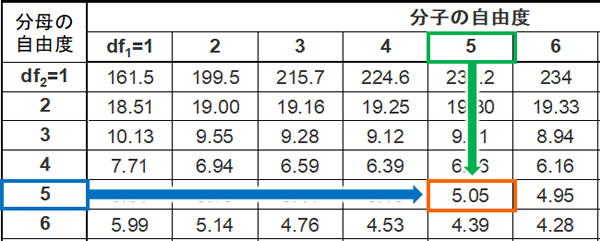
こうして、有意水準が0.05となるF値は5.05であるとわかりました。つまりF値が5.05よりも大きい場合、5%以下の確率で発生する稀なケースが起こったと判断できます。
それでは、計算したF値と比較してみましょう。前述の通り、標本Aと標本BのF値は2.202です。そのため、有意水準が0.05となるF値(5.05)よりも小さい値です。そのため今回の結果は偶然に起こったケースであり、帰無仮説を棄却することができません。

そこで帰無仮説を採用し、2つの標本にはデータのばらつきに差がないと結論付けることができます。つまり2つの標本は等分散です。
F検定を利用し、2つの標本が等分散かどうかを確認する
統計学を学ぶとき、すべての人がスチューデントのt検定を学びます。t検定は最も頻繁に利用されている統計手法です。
ただ二標本t検定をするためには、事前にデータが等分散かどうかを確認しなければいけません。そこで二標本t検定をする前にF検定をしましょう。帰無仮説を採用でき、等分散であると確認できれば、スチューデントのt分布を利用できます。
なおF検定を理解するためには、必ずF分布を学ばなければいけません。2つの標本の比について、確率分布を表したものがF分布です。F分布の形は自由度によって変わります。95%信頼区間は既にわかっているため、自由度とF分布表を利用することで有意水準0.05となるF値を確認しましょう。
こうしてp値を計算し、F分布を利用することによってF検定をすることができます。データの形が同じかどうかを確認するため、F検定を行いましょう。






