複数の要素が関係しているとき、どの要素に大きく影響を受けるのか解析する手法が多変量解析です。多変量解析の中でも、最も重要な分野の一つが重回帰分析です。
重回帰分析をすることによって、将来の結果を予測することができます。多くの場合、複数の要因が関係することで結果を得られます。そこで「どの要素が優れる結果につながるのか」を知ることができれば、どのような行動を取ればいいのかわかります。
それでは、どのように重回帰分析をすればいいのでしょうか。詳しい計算方法を理解する必要はないものの、大まかな概要を学べば、重回帰分析によって得られる回帰方程式の意味を理解できるようになります。
多くの人にとって重回帰分析は重要です。そこで、どのように重回帰分析をすればいいのか統計学の立場から解説していきます。
もくじ
単回帰分析と重回帰分析の違い:多変量解析
回帰分析を学ぶとき、最初に学習するのが単回帰分析です。2つの因子について、どのような相関があるのか直線を利用して回帰式を得るのです。例えば売上と広告費について、以下のようなグラフを利用して回帰直線の式を得ます。
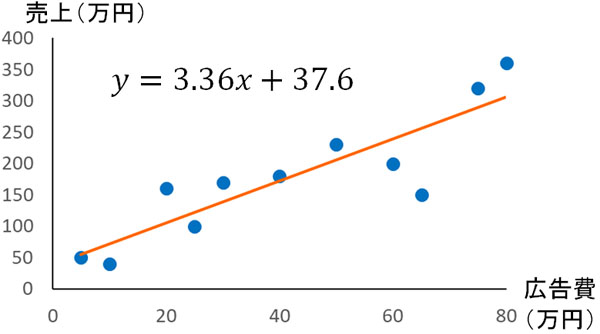
2つの因子の相関関係を分析する手法を単回帰分析といいます。一方で要因が2つではなく、3つ以上になるケースは多いです。その場合は単回帰分析ではなく、重回帰分析と呼ばれます。
実際のところ、多くの要因によって結果が決まるケースは多いです。例えば売上を決定する要因は広告費だけではありません。実際には以下の要素も関係しています。
- 市場シェアの割合
- 営業マンの人数
- 商品開発力(特許の数など)
複数の要素によって結果を得られるため、何が影響しているのか確かめる必要があります。そこで2つ以上の要因によって結果が変化するとき、その中身を解析する手法が多変量解析です。相関と回帰を利用することで分析する重回帰分析というのは、多変量解析の一つです。
なお単回帰分析も多変量解析の一種です。多変量解析の中でも最も単純な単回帰分析を学んでいれば、重回帰分析をより理解しやすくなります。
重相関係数により、因子同士の相関関係を得る
重回帰分析をするとき、得られるのが重相関係数です。重相関係数とは、ピアソンの相関係数と同じと理解しましょう。世間一般的に利用されている相関というのは、ピアソンの相関係数を指します。
例えば広告費と売上について、ピアソンの相関係数rが0.9の場合、非常に強い相関があると判断できます(相関係数は\(-1≦r≦1\)の範囲)。
一方で重回帰分析では、複数の相関係数を得ることができます。例えば売上について、以下の要因がどのように関係しているのか確認したいとします。
- 売上
- 広告費
- 市場シェア
この場合、3つの要素が関係しています。そのため、「売上と広告費の相関」「売上と市場シェアの相関」「広告費と市場シェアの相関」と3つの相関があります。
それぞれの相関関係を確認することによって、どの要素が関係しているのか把握できます。例えば売上と市場シェアは強い相関があるものの、売上と広告費には相関がないかもしれません。この場合、広告費を大幅に減らして市場シェアの拡大に注力するほうが売り上げを伸ばしやすくなります。
重相関係数の確認が重要なのは、どの因子が結果(今回の場合は売上)と深く関係しているのか把握できるようになるからなのです。
最小二乗法を利用した回帰方程式により、将来の結果を予測する
また回帰分析では直線を利用することによって将来の結果を予測します。単回帰分析であれば、2つの要素を分析するため、\(y=ax+b\)の式になります。例えば売上と広告費の回帰分析は以下の式になります。
- 売上=広告費\(×x+b\)
この式を得ることができれば、広告費をいくら使えば目的とする売り上げを達成できるのか予測できるようになります。
一方で重回帰の場合、複数の要因が関係しているため、それぞれの要素を考慮する必要があります。例えば売上、広告費、市場シェア、商品開発力の式を得たい場合、以下のようになります。
- 売上=広告費\(×x_1+\)市場シェア\(×x_2+\)商品開発力\(×x_3\)\(+b\)
売上を構成する要素について、このように複数の要素を利用することによって式を出します。重回帰分析で得られる式は以下のように表されます。
- \(y=ax_1+bx_2+cx_3+\)\(…+\)定数
要素の数が多くなると、その分だけ式が長くなります。ただ、概念はそこまで難しくありません。
なお、どのように直線の式を計算するかというと最小二乗法を利用します。最小二乗法では、「回帰直線上の点」と「実測データとの距離」の差を出します。これを残差といいます。
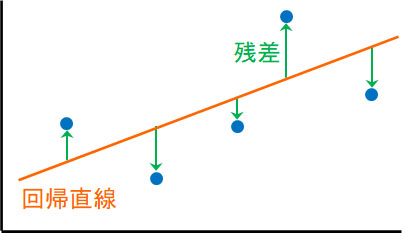
ただ残差にはプラスとマイナスがあり、すべて足すと必ず答えは0になります。そこで残差を二乗し、すべてプラスに変えましょう。その後、すべての残差を足して答えが最小になるようにします。これが最小二乗法によって式を得るやり方です。
例えば要素が2つの場合、5番目の点の\(y\)座標は\(y_5\)です。また、回帰直線上の点の座標は\(ax_5+b\)です。そのため、残差は\(y_5-(ax_5+b)\)です。
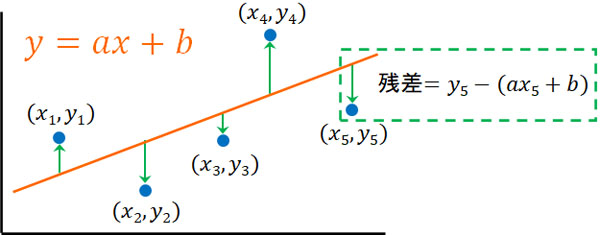
次に、すべての残差を二乗して足しましょう。この場合、以下の式になります。
\((y_1-ax_1-b)^2\)\(+(y_2-ax_2-b)^2\)\(+(y_3-ax_3-b)^2…\)
\(=\displaystyle\sum{(y_i-ax_i-b)^2}\)
そこで、この式の答えが最小になるようにすれば傾き\(a\)と切片\(b\)を求めることができます。
なお重回帰分析では、要素が3つ以上になります。例えば要素が3つの場合、5番目の点の\(y\)座標は\(y_5\)であり、回帰直線上の点の座標は\(ax_5+bx_5+c\)です。そのため、残差は\(y_5-(ax_5+bx_5+c)\)です。
そこで、すべての残差を二乗して足しましょう。
\((y_1-ax_1\)\(-bx_1-c)^2\)\(+(y_2-ax_2\)\(-bx_2-c)^2…\)
\(=\displaystyle\sum{(y_i-ax_i-bx_i-c)^2}\)
その後、最小値となる\(a\)や\(b\)、\(c\)の値を計算しましょう。これが重回帰分析で式を得る方法です。
実際の式を得る過程や公式については、微分や行列を利用する必要があるので省きます。表計算ソフトを用いれば重回帰の式を出してくれます。そのため、統計処理するときは最小二乗法の理論を理解できていれば問題ありません。
最小二乗法を利用して回帰直線の式を得る公式の出し方については、より深く学びたい人が大学数学を学んだあとに挑戦しましょう。
平均、分散(標準偏差)、共分散を利用して相関係数を求める
それでは、重回帰分析を利用して相関係数を計算しましょう。実際の計算は表計算ソフトがしてくれます。ただ理論を理解するため、重回帰分析の手順を学ぶことは重要です。
相関係数を得るとき、ピアソンの相関係数では共分散Sxyを利用したと思います。まず、一つのデータについて偏差(ばらつき)を出します。その後、すべての偏差を平均化することによって共分散Sxyを得ます。
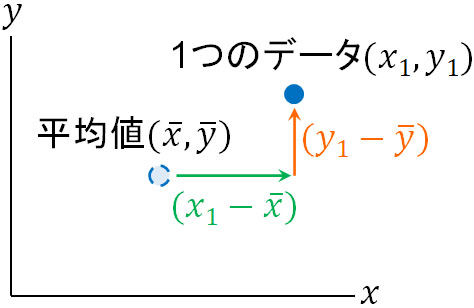
そのため、共分散は以下の式によって計算することができます。
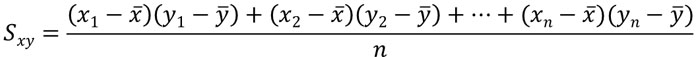
- Sxy:共分散
- \(x_1\)や\(x_2\)など:それぞれのデータの値
- \(\overline{x},\overline{y}\):\(x\)や\(y\)の平均値
- n:データの数
ピアソンの相関係数を学んでいる場合、共分散の概念や公式については既に理解していると思います。
なお重回帰分析の場合、要因は複数あります。例えば売上A、広告費B、市場シェアCについて相関係数を求めたい場合、以下のようにそれぞれ相関係数を計算します。

先ほどとまったく同じ式になりますが、それぞれの要素ごとに平均値と各データ、データ数を利用して共分散を出しましょう。
またピアソンの相関係数では以下のように相関係数rを出しました。

同じように、共分散と分散(標準偏差)を利用することによって重相関係数をそれぞれ出しましょう。

重回帰分析のように要素が多くなっても、相関係数の計算方法は同じです。そのためピアソンの相関係数を学んでいる場合、重相関係数の出し方を理解するのは難しくないはずです。
例題を利用し、重相関係数を得る
それでは、表計算ソフトを利用せずに重相関係数を計算してみましょう。例えば会社の売上について、商品ごとの売上と広告費、市場シェアの関係が以下の通りだとします。
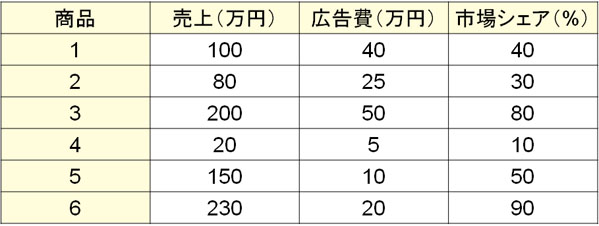
そこで、「売上と広告費」「売上と市場シェア」について重相関係数を計算してみましょう。まず、以下の表を作ります。
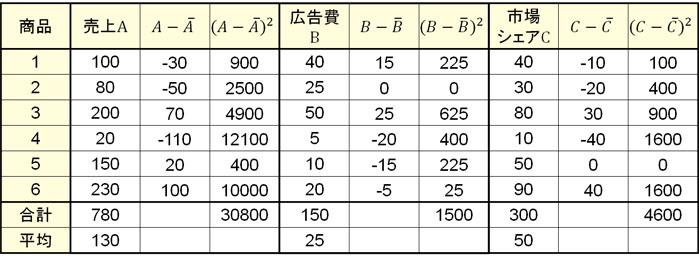
これにより売上A、広告費B、市場シェアCの平均値と分散(標準偏差)がわかります。
・売上Aの分散と標準偏差
売上Aの分散\(=\displaystyle\frac{30800}{6}≒5133.33\)
売上Aの標準偏差\(=\sqrt{5133.33}≒71.65\)
・広告費Bの分散と標準偏差
広告費Bの分散\(=\displaystyle\frac{1500}{6}=250\)
広告費Bの標準偏差\(=\sqrt{250}≒15.81\)
・市場シェアCの分散と標準偏差
市場シェアCの分散\(=\displaystyle\frac{4600}{6}≒766.67\)
市場シェアCの標準偏差\(=\sqrt{766.67}≒27.69\)
次に、共分散SABと共分散SACを計算しましょう。以下の表を作ります。
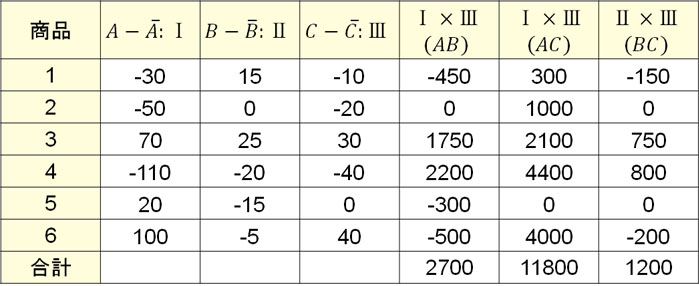
表より、共分散SABと共分散SACは以下のようになります。
\(S_{AB}=\displaystyle\frac{2700}{6}=450\)
\(S_{AC}=\displaystyle\frac{11800}{6}≒1966.67\)
※参考までに、\(S_{BC}=\displaystyle\frac{1200}{6}=200\)
こうして共分散を求めることができれば、それぞれの重相関係数rを得ることができます。
\(r_{AB}=\displaystyle\frac{450}{71.65×15.81}≒0.397\)
\(r_{AC}=\displaystyle\frac{1966.67}{71.65×27.69}≒0.991\)
こうして、AB(売上と広告費)の相関は0.397と低いことがわかります。一方でAC(売上と市場シェア)の相関は0.991と非常に高いです。そのためこの結果では、広告費をできるだけ減らし、市場シェアを取ることを考えれば売り上げを伸ばせることがわかります。
実際の計算は表計算ソフトが行うものの、このような計算方法によって重相関係数を得ることを理解しましょう。
重回帰の式の計算:回帰方程式を表計算ソフトで計算する
なお重回帰の式を得るときについても、表計算ソフトを用いて行います。例えば因子が3つであり、売上Aを\(z\)、広告費Bを\(x\)、市場シェアCを\(y\)とすると以下の回帰方程式になります。
- \(z=ax+by+c\)
そこで係数\(a,b,c\)を計算しましょう。計算式は非常に複雑なため、手計算ではなくすべての計算を表計算ソフトに任せましょう。今回のデータの場合、以下の結果になります。
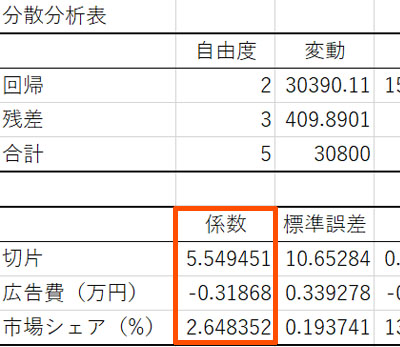
表計算ソフトを利用して計算した結果、係数を出すことができました。\(z=ax+by+c\)に当てはめると以下のようになります。
- \(z=-0.32x+2.65y+5.55\)
このように式を確認すると、広告費を出してもまったく売上に貢献しないことがわかります。そのため、広告を出すのをやめたり、広告を出す方法を大幅に変えたりしなければいけません。
また市場シェアが1%増えると、それに伴って2.65万円の売上増を見込めます。そのためシェア拡大の戦略を採用するのは優れているとわかります。
なお表計算ソフトには、下限95%や上限95%が記されています。これは95%信頼区間を意味します。つまり、「100回くらい実施すれば95回は真の値がこの中に含まれる」ことになります。先ほどのデータについて、下限95%や上限95%は以下のように表計算ソフトで計算されています。
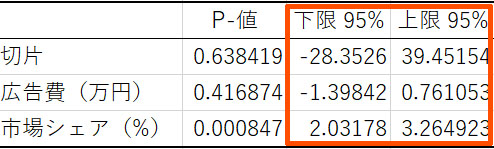
そのため広告費の傾き\(a\)と市場シェアの傾き\(b\)の95%信頼区間は以下のようになります。
- \(-1.398<a<0.761\)
- \(2.032<b<3.265\)
広告費の傾き\(a\)については、95%信頼区間に0を含みます。そのため、広告費を出しても売り上げへの貢献度合いはゼロである可能性があります。
一方で市場シェアの傾き\(b\)については、95%信頼区間に0を含みません。ここからも、このデータでは「市場シェアを伸ばすことによって売上アップにつながる」ことがわかります。
このように重回帰分析をすることによって、どの要素が影響しているのかわかるようになります。あらゆる分野で重回帰分析が利用されているのはこうした理由があるのです。
重回帰分析の理論を理解し、統計データを解析する
多くの要素の関わりによって結果を得られることはよくあります。そうしたとき、重回帰分析を利用しましょう。重回帰分析によって、どの要素が相関をもち、結果に関与しているのか把握できます。また、結果に影響しなかったり、マイナスの影響を与えたりする要素もわかります。
データの相関や回帰を解析することが重要なのは、どの要因が結果に大きな影響を与えるのか調べることができるからです。このとき重要な解析法が重回帰分析です。
重相関係数を利用し、どの要素が結果と結びついているのか確認しましょう。また重回帰の式を得ることによって、将来の結果を予測できるようになりましょう。
あらゆる分野で利用されているのが重回帰分析です。表計算ソフトを利用することによって、一瞬で結果を得ることが可能です。ただ最小二乗法や共分散の概念を学ぶことにより、重回帰分析をより深く理解しましょう。






