ウェルチのt検定：等分散でない場合のt検定と統計量・自由度の公式

統計学で最も利用される方法がt検定です。ただt検定には複数の種類があります。その中でも特に有名なのがスチューデントのt検定です。最初に発見されたt検定がスチューデントのt検定になります。

ただt検定では、等分散でなければいけないというデメリットがあります。そこでスチューデントのt検定を改良させた方法にウェルチのt検定があります。ウェルチのt検定を利用する場合、等分散の確認は不要です。

それでは、どのようにウェルチのt検定を利用すればいいのでしょうか。公式はどのようになっているのでしょうか。

統計処理でウェルチのt検定を行うのは一般的であり、多くの人に利用されています。そこで統計処理をするとき、どのようにウェルチのt検定を利用すればいいのか理解しましょう。

1 等分散かどうかの確認が不要なウェルチのt検定
- 1.1 ウェルチのt検定では、F検定やスチューデントのt検定を省ける
2 ウェルチのt検定の公式
- 2.1 ウェルチのt検定では自由度の公式が複雑
- 2.2 ウェルチのt検定で計算する例題
3 ウェルチのt検定を利用して統計処理する

等分散かどうかの確認が不要なウェルチのt検定

最も有名な検定法がスチューデントのt検定です。ただ二標本t検定をするとき、データが正規分布していることに加えて、2つのデータが等分散でなければいけません。

等分散というのは、要はグラフの形が同じであることを指します。一方でグラフの形が異なる場合、不等分散です。

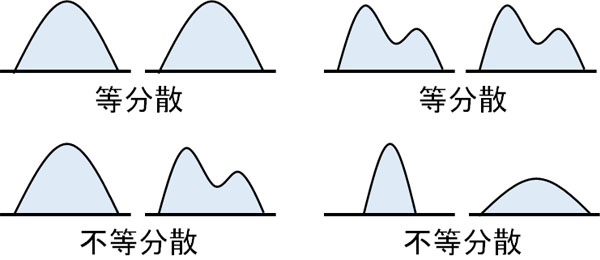
等分散かどうかを確認する手法がF検定です。F検定によって2つのデータが等分散かどうかを確認し、等分散であるとわかればスチューデントのt検定を利用できます。

そのためスチューデントのt検定をするためには、必ず以下の手順になります。

F検定を行い、等分散であることを確認する
等分散であるとわかれば、スチューデントのt検定を行う

それでは、二標本t検定をするときに2つのデータが等分散でない場合はどのようにすればいいのでしょうか。この場合ウェルチのt検定を利用します。

ウェルチのt検定では、F検定やスチューデントのt検定を省ける

ウェルチのt検定を利用して二標本t検定をする場合、2つのデータが等分散かどうかに関係なくt検定をすることができます。等分散である場合は当然ながらウェルチのt検定をすることができます。また等分散でない場合であっても、ウェルチのt検定を利用してもいいです。

そのため、F検定をして等分散でないとわかった場合、スチューデントのt検定ではなく、ウェルチのt検定を利用します。

・最初に必ずF検定をしないといけないのか

なお教科書的には、F検定をして等分散でないとわかった場合、ウェルチのt検定をします。ただ最初からウェルチのt検定をしても問題ありません。この場合であれば、F検定を省くことができます。

統計では、何度も検定をしてはいけないというルールがあります。同じデータを利用するとき、ある検定法では「差がない」という結果であったとしても、ほかの検定法では「有意差がある」という結果になるケースがあります。これを多重性の問題といいます。

複数の検定を試す場合、そのうち一つは有意差をもつ結果を得られることがあります。ただ本来は差がなにも関わらず、都合のよい結果を得るため、複数の方法を利用して統計処理をしてはいけません。

こうした多重性の問題があるため、F検定やスチューデントのt検定を行わず、ウェルチのt検定のみをしても問題ないというわけです。

ウェルチのt検定の公式

それでは、実際にウェルチのt検定をしてみましょう。検定の方法はスチューデントのt検定と同じです。有意水準とp値を比較することによって、差があるかどうかを確かめるのです。

つまり自由度を利用して統計量Tを計算し、有意水準0.05（または有意水準0.01）となるT値と比較し、差があるかどうかを確認しましょう。

このとき、ウェルチのt検定ではスチューデントのt検定と比べて少し公式が異なります。対応のある二標本t検定をするときのスチューデントのt検定について、ウェルチのt検定での公式と比べると以下のようになります。

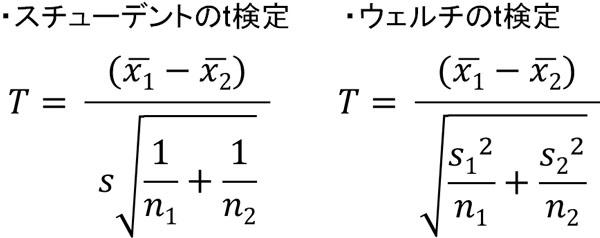
このように、統計量Tを出す公式はほとんど同じです。スチューデントのt検定では、2つのデータを合わせた分散（標準偏差）を利用して統計量Tを計算します。一方でウェルチのT検定では、それぞれのデータについて分散（標準偏差）を計算することで統計量Tを計算します。

そのためスチューデントのt検定のやり方を理解している場合、ウェルチのt検定を学ぶときに新たな理論や方法を覚える必要はありません。利用する公式はほとんど同じですし、検定をするときの手順に大きな違いはありません。

ウェルチのt検定では自由度の公式が複雑

一方で自由度の計算方法は大きく異なります。スチューデントのt検定であれば、自由度\(n-1\)のt分布を利用します。つまりサンプル数から1を引くことで自由度を得ることができます（対応のない二標本t検定の場合、自由は\(n_1+n_2-2\)となります）。

一方でウェルチのt検定を利用する場合、自由度\(d\)の計算方法が非常に複雑になります。具体的には、以下の公式を利用することによって自由度を求めます。

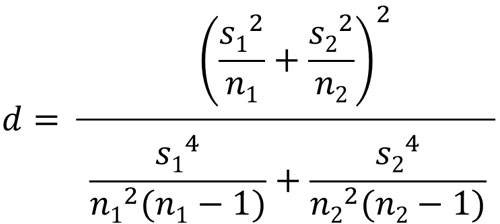
当然ながら、この公式を覚える必要はありません。自由度はコンピューターが計算してくれるため、あなたが公式を利用して計算しなくてもいいのです。

なおウェルチのt検定を利用する場合、自由度\(d\)は小数点で答えを得られます。そこで四捨五入をして自由度を整数に変換し、有意水準0.05（または有意水準0.01）となるT値を探すといいです。

ウェルチのt検定で計算する例題

それでは、実際にウェルチのt検定を利用して計算してみましょう。方法はスチューデントのt検定と同じであり、利用する公式が違うだけです。例えば、以下の問題の答えは何でしょうか。

数学のテストを実施しました。AクラスとBクラスの点数が以下のとき、AクラスとBクラスに学力差はあるでしょうか。

Aクラス	Bクラス
50	70
48	62
40	55
38	65
66	52
58	68

帰無仮説と対立仮説は以下のようになります。

帰無仮説：2つのクラスに差はない
対立仮説：2つのクラスに差がある

それぞれの事象について、まとめると以下のようになります。

	Aクラス	Bクラス
サンプル数\(n\)	6	6
標本平均\(\overline{x}\)	50	62
分散（不偏分散）\(s^2\)	113.6	51.6
標準偏差（不偏標準偏差）\(s\)	10.66	7.18

そこで、公式を利用して統計量Tを計算しましょう。以下のようになります。

\(T=\displaystyle\frac{\overline{x_1}-\overline{x_2}}{\sqrt{\displaystyle\frac{(s_1)^2}{n_1}+\displaystyle\frac{(s_2)^2}{n_2}}}\)

\(T=\displaystyle\frac{50-62}{\sqrt{\displaystyle\frac{113.6}{6}+\displaystyle\frac{51.6}{6}}}\)

\(T≒-2.287\)

参考までに、スチューデントのT検定で計算しても\(T≒-2.287\)となります。そのため当然ではありますが、スチューデントのt検定でもウェルチのt検定でも得られる統計量Tは値が似ています。

次に自由度\(d\)を計算しましょう。公式に当てはめると以下のようになります。

\(d=\displaystyle\frac{\left(\displaystyle\frac{113.6}{6}+\displaystyle\frac{51.6}{6}\right)^2}{\displaystyle\frac{113.6^2}{6^2×5}+\displaystyle\frac{51.6^2}{6^2×5}}\)

\(d≒8.765\)

四捨五入して、自由度9で有意水準を確認しましょう。自由度9のとき、\(P=0.05\)となるT値は2.262です。つまり\(-2.262≦T≦2.262\)の場合、偶然に起こった事象と考えることができます。

ただ統計量Tは-2.287であり、\(-2.262≦T≦2.262\)に含まれていません。そのため5%以下で発生する稀な事象と考え、帰無仮説を棄却します。そこで対立仮説を採用し、「2つのクラスには数学の学力に差がある」と考えます。

参考までにスチューデントのt検定を利用する場合、今回の問題だと自由度は10です。そのため今回の問題では、スチューデントのt検定に比べて、ウェルチのt検定では少ない値での自由度を利用して計算をしました。

スチューデントのt検定でもウェルチのt検定でも、今回の問題については両方とも「差がある」という結果になります。ただ利用する公式が違う場合、スチューデントのt検定とウェルチのt検定で結果が異なるケースがあることを理解しましょう。多重性の問題を回避する必要があるのは、利用する検定法によって得られる結果が異なるケースがあるからなのです。