ガンマ分布：確率密度関数での計算や期待値（平均）・分散の公式

任意の時間にイベントが何回発生するのかを表すのがガンマ分布です。非常に多くの場面で利用されるのがガンマ分布になります。

指数分布と似ているのがガンマ分布です。また指数分布を一般化させ、より多くのケースで利用できるようにしたのがガンマ分布です。人の体重分布やウイルスの潜伏期間など、ガンマ分布に従うケースは多いです。

そこでガンマ分布の性質を理解しましょう。確率密度関数を学び、期待値（平均）や分散を計算できるようにするのです。

ガンマ分布を利用すれば、さまざまな場面で確率を予想できるようになります。そこで、ガンマ分布の性質や期待値・分散を得る方法を解説していきます。

1 特定期間に\(n\)回起こる確率を表すのがガンマ分布
- 1.1 ガンマ分布と指数分布の関係：ポアソン分布との違い
2 ガンマ分布の確率密度関数
3 アーラン分布はガンマ分布の一部
4 ガンマ分布を利用して時間ごとの確率を得る

特定期間に\(n\)回起こる確率を表すのがガンマ分布

連続型確率分布の一つがガンマ分布です。ガンマ分布とは、「期間\(λ\)ごとに1回起こるランダムなイベントについて、イベントが\(n\)回発生する時間分布」を指します。

ガンマ分布に従うケースは非常に多く、例えば以下の分布はガンマ分布に従います。

人の体重分布
ウイルスの潜伏期間
保険金の支払い額
電子機器の寿命

他にも多くの場面でガンマ分布が利用されます。特定の期間にイベントが何回発生するのかを利用することによって、さまざまな統計処理をすることができるのです。

例えば、1分あたり10人が訪れる公園があるとします。訪問者が50人になる時間はいくらでしょうか。この場合、以下のようなガンマ分布となります。

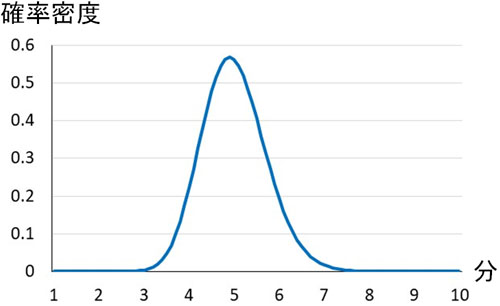
1分あたり10人が訪れるため、5分で50人になると容易に予想できます。ただ実際には4分で50人になることもあるし、6分で50人になることもあります。そこでガンマ分布を用いて図にすると、どれくらいの確率密度なのか把握できます。

図を確認すると、2分で50人が訪れる可能性はほぼ0とわかります。一方、4～6分で公園に50人集まる可能性が高いとわかります。ガンマ図を利用することによって、将来の結果を予測することができるのです。

ガンマ分布と指数分布の関係：ポアソン分布との違い

それでは、ガンマ分布はほかの分布と何が異なるのでしょうか。まずは、指数分布との違いを理解しましょう。前述の通り、指数分布を一般化させた分布がガンマ分布です。ガンマ分布は指数分布の一種なのです。

指数分布の場合、定期的に発生するランダムなイベントが一回発生する確率について、いつ起こるのかを得ることができます。ただイベントが一回発生するケースを調べることができても利用しにくいです。多くの場合、イベントが一回ではなく、複数回起こるケースを知りたいです。

そこで「定期的に発生するランダムなイベント」が平均して\(λ\)回発生するとき、特定の時間に合計\(n\)回起こる確率を調べられるのがガンマ分布です。指数分布よりもガンマ分布が利用されるのは、利用範囲が非常に広いからです。

・ポアソン分布との違い

ガンマ分布と指数分布との違いを理解した後、ポアソン分布との違いを学びましょう。ガンマ分布と指数分布は親せきであるため、ポアソン分布との違いを理解するためには、指数分布とポアソン分布の違いに着目すればいいです。

ガンマ分布や指数分布というのは、発生間隔に着目します。例えば指数分布の場合、次のイベント発生がいつなのかを知ることができます。一方でポアソン分布の場合、特定の時間内に発生するイベント回数に着目します。

指数分布：次の発生間隔に着目する
ポアソン分布：特定の時間内に発生するイベント回数に着目する

ガンマ分布や指数分布で知ることができるのは時間ごとの確率分布です。一方、ポアソン分布ではイベントの発生回数を調べることができます。

ガンマ分布の確率密度関数

次に、ガンマ分布の確率密度関数を確認しましょう。それぞれの記号（パラメータ）の意味を以下のように設定します。

\(x\)：経過時間
\(λ\)：特定期間でイベントが発生する平均回数
\(a\)：事象が起こる回数
\(Γ(a)\)：係数

このとき、ガンマ分布の確率密度関数\(f(x)\)は以下になります。

\(f(x)=\displaystyle\frac{λ^a}{Γ(a)}x^{a-1}e^{-λx}\)

公式は複雑であるため、公式をみても意味を理解できないと思います。ただ「公式に値を当てはめることによって、ガンマ分布の確率密度を得られる」と理解できればそれで充分です。

なお\(Γ(a)\)はガンマ関数であり、\(f(x)\)を積分して1になるように定められています。ガンマ関数の計算は複雑です。ただ事象が起こる回数\(a\)が正の整数の場合、\(Γ(a)=(a-1)!\)になります。この場合、計算が簡単です。

それでは、先ほどの例題について値を当てはめてみましょう。

1分あたり10人が訪れる公園があるとします。4分後に訪問者が50人になる確率密度はいくらでしょうか。

4分後の確率密度を計算してみましょう。1分を時間の基準にすると、以下のようになります。

\(x\)：4
\(λ\)：10
\(a\)：50
\(Γ(a)\)：49!

計算式は以下です。

\(f(4)=\displaystyle\frac{10^{50}}{49!}×4^{49}×e^{-10×4}\)

\(≒0.2213\)

こうして、4分後の確率密度は0.2213とわかります。確率密度関数を利用し、値を代入することによって「特定の時間にイベントが発生する確率密度」を得られるようになります。

累積分布関数を利用して確率を計算する

なお指数分布にも共通しますが、特定の時間の確率密度を得られても意味がありません。そうではなく、それまでの確率の累積を確認するほうが重要です。それまでに発生するすべての確率密度を足せば、特定の時間が経過するまでに、イベントが\(n\)回発生する確率を得られるようになります。

そこで、確率密度関数を利用して面積を計算しましょう。特定の時間について、それまでの確率密度の面積を計算すれば、合計の発生確率を計算できます。これを累積分布関数\(F(x)\)といいます。

ガンマ分布の累積分布関数は非常に複雑なので、表計算ソフトを利用して計算しましょう。先ほどの例題であれば、累積分布関数の結果は以下のようになります。

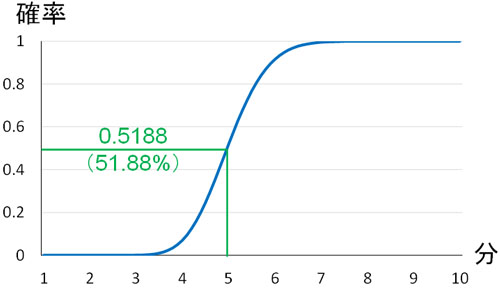
例えば5分経過時間の値を確認すると、0.5188（51.88%）です。3分後や4分後に公園に50人が訪れるケースもあります。そこでこれらのケースも含める場合、5分後に50人が訪れる確率は50%よりも大きくなります。

また確率をすべて足す場合、当然ながら1（100%）になります。そのため、時間経過と共に値は1に近づきます。

ガンマ分布で期待値（平均）を得る公式

それでは、ガンマ分布での期待値（平均）はどのようにして得られるのでしょうか。特定期間でイベントが発生する平均回数を\(λ\)、事象が起こる回数を\(a\)とすると、ガンマ分布の期待値\(E(X)\)は以下の公式になります。

\(E(X)=\displaystyle\frac{a}{λ}\)

このように、シンプルな公式です。なお期待値については、指数分布と同様に、なぜこのような公式になるのか理解しやすいです。

例えば1分間に平均5人（\(λ\)）が訪れる公園であれば、5人（\(a\)）が訪れる期待値は当然ながら1分です。一方、10人（\(a\)）が訪れる期待値は\(\displaystyle\frac{10}{5}=2\)分です。事象が起こる回数\(a\)が増えると、その分だけ期待値（達成に必要な時間）は大きくなります。

なお、ガンマ分布の期待値の証明はここでは行いません。証明をしたい場合、期待値の定義を利用して計算してみてください。