統計学で学ぶ分野の一つがポアソン分布です。正規分布や二項分布を学んだあと、ポアソン分布について習うことが多いです。
それでは、ポアソン分布は正規分布と何が違うのでしょうか。また、どのようなときにポアソン分布が利用されるのでしょうか。
ポアソン分布というのは、起こる確率が非常に低い場合に利用されます。またサンプル数がわからなかったとしても、期待値(平均)や事象が起こる回数を利用することによって確率の計算ができるため、ポアソン分布の活用は便利な方法でもあります。
そこで、ポアソン分布の使い方を理解しましょう。どのようにポアソン分布を利用し、確率の計算をすればいいのか解説していきます。
もくじ
二項分布は正規分布だけでなく、ポアソン分布にも近似できる
ポアソン分布について理解するため、二項分布について復習しましょう。多くの場合、世の中の事象は二択です。以下のように、二択を比較するケースは多いです。
- 死亡事故が起こるのか、起こらないのか
- 不良品が発生するのか、発生しないのか
- 薬が効くのか、効かないのか
こうした二択について、統計学では二項分布を利用します。また二項分布は正規分布へ近似できます。つまり二項分布(二択のデータ)について、正規分布しているとみなして確率を計算することができます。
また二項分布については、正規分布へ近似できるだけでなく、ポアソン分布へ近似することもできます。つまり二択の選択について、ポアソン分布とみなして確率を計算してもいいのです。正規分布を利用して確率を計算できるものの、場合によってはポアソン分布を利用するほうが優れるケースもあります。
起こる確率が低いとき、ポアソン分布が利用される
それでは、ポアソン分布とはどのようなケースで利用される統計手法なのでしょうか。ポアソン分布というのは、前述の通り起こる確率が非常に低いときに利用されます。つまり起こるかどうかはわからないものの、一定の確率で発生する場合、ポアソン分布を利用します。
より具体的には、試行回数が1万以上と多かったり、起こる確率が\(\displaystyle\frac{1}{10000}\)などのように小さかったりするとき、ポアソン分布が有効です。
例えば死亡事故であれば、発生確率は非常に小さいです。ただ毎日、どこかで死亡事故が起きています。工場での不良品についても、不良品発生率は低いものの必ず不良品は発生します。「薬が効くかどうか」であれば、何万人もの人に対して治験をして効くかどうかを判断します。
いずれにしても、発生する確率は非常に小さいものの、一定の確率で発生する場合、ポアソン分布を利用できるというわけです。
「二項分布について、ポアソン分布に近似できる」といわれると、難しいように感じてしまいます。ただ、「ほとんど起こらない事象の確率を計算するためのツールがポアソン分布」と理解すればわかりやすいです。
例えば、ランダムに起きる事故や病気の発症などでポアソン分布が頻繁に利用されます。こうした稀に起こる事象では、ポアソン分布を利用するのが有効なのです。
二項分布の式を変形し、極限を利用してポアソン分布の公式を得る
それでは、実際にポアソン分布の公式を確認しましょう。ポアソン分布は二項分布を発展させた内容です。そこで、二項分布の公式を変形しましょう。
二項分布では反復試行の確率を計算します。二択の試行について、\(n\)回のデータを取るとき、\(p\)の確率で\(k\)回起こるときの確率は以下の公式で表されます。
\(_nC_kp^k(1-p)^{n-k}\)
※反復試行の確率や二項分布について理解している前提で話を進めるため、理解していない人はこれらの内容を事前に学びましょう。
例えばサイコロを100回投げ、1の目が10回出る確率は以下の式によって計算できます。
\(_{100}C_{10}\left(\displaystyle\frac{1}{6}\right)^{10}\left(\displaystyle\frac{5}{6}\right)^{90}\)
それでは、特定の期間に「平均して\(λ\)回起こる事象」について、\(k\)回起こる確率はいくらになるでしょうか。
二項分布では試行回数\(n\)と起こる確率\(p\)を利用し、平均(期待値)\(λ\)を以下の公式によって得られます。
\(λ=np\)
これを変形すると以下のようになります。
\(p=\displaystyle\frac{λ}{n}\)
そこで、二項分布の公式に対して\(p=\displaystyle\frac{λ}{n}\)を代入すると以下のようになります。
\(_nC_k\left(\displaystyle\frac{λ}{n}\right)^k\left(1-\displaystyle\frac{λ}{n}\right)^{n-k}\)
それでは、確率\(p\)が非常に小さい場合(試行回数\(n\)が非常に大きい場合)では、この公式はどのように変換できるでしょうか。
\(n\)の値を極限まで数字を大きくするとき\(\displaystyle \lim_{ n \to \infty }\)と表します。ポアソン分布では\(n\)の値が非常に大きいため、\(\displaystyle \lim_{ n \to \infty }\)を利用して公式を以下のように変形しましょう。
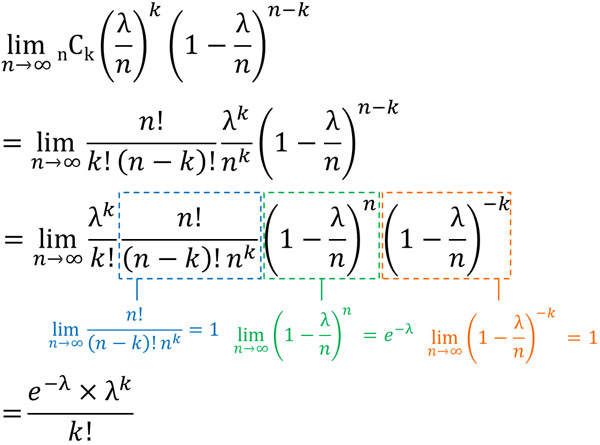
こうして、ポアソン分布の公式を得ることができました。\(e\)はネイピア数であり、\(e=2.7182…\)です。つまり定数であり、「平均(期待値)である\(λ\)」と「起こる回数である\(k\)」を代入すれば、確率を計算することができます。
サンプル数がわからなくても確率の計算が可能
それではポアソン分布で重要な点は何でしょうか。それは、公式の中に試行回数\(n\)が含まれていないことです。つまりサンプル数がわからなかったとしても、確率の計算をすることができるのです。
本来、確率を計算するときはサンプル数(試行回数)を利用します。事実、二項分布を正規分布へ近似する場合、試行回数は重要です。一方で二項分布をポアソン分布へ近似する場合、期待値と発生回数のみを利用することで発生確率を計算できるというわけです。
前述の通り、ポアソン分布では試行回数が非常に多い(または発生確率が非常に小さい)という場合に利用できます。そのため極限を利用し、試行回数\(n\)を公式から消すことができたのです。
ポアソン分布の例題を解き、確率を計算する
それでは、実際にポアソン分布を利用することによって確率を計算してみましょう。以下の例題の答えは何でしょうか。
- 1時間に平均して3回、コールセンターに電話がかかってきます。1時間に9回、電話がかかってくる確率はいくらでしょうか。
期待値\(λ\)は3であり、発生回数\(k\)は9です。そこで、以下の計算をしましょう。
\(\displaystyle\frac{3^9×{2.7182}^{-3}}{9!}≒0.002701\)
こうして、発生確率は約0.27%であるとわかります。参考までに、\(λ=3\)の場合、\(k\)が0~10のときの確率は以下のようになります。
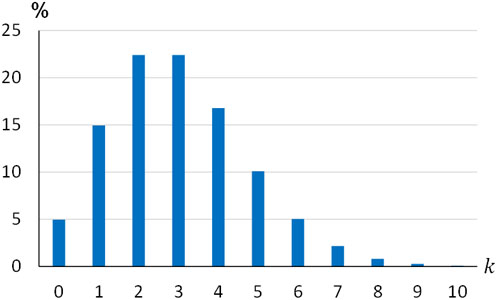
このグラフより、1時間にまったく電話がかかってこない確率は5%です。また「1時間に平均して3回の電話がある」とわかっている場合であっても、1時間に2回の電話がある確率と1時間に3回の電話がある確率は同じです。
このようにポアソン分布を利用することによって、特定の頻度で発生する確率を求めることができます。
なおポアソン分布を利用するとき、「一定割合でランダムに発生する場合であれば確率を計算できるものの、そうでない場合は正しく確率を計算できない」という弱点があります。
例えば生命保険会社がポアソン分布を利用し、保険商品を販売するとします。ただ国内で大規模な災害が発生し、一般市民を含めて多数の死傷者が出た場合、保険金を支払う対象の人は非常に多くなってしまいます。
このように特定の要因と強い相関関係がある場合、ポアソン分布で予測することができません。ポアソン分布というのは、あくまでもランダムに発生するケースにのみ利用できます。ポアソン分布を利用して確率を計算したとしても、完ぺきではないのです。
ランダム性が強いほどポアソン分布の効果が強くなります。ただ災害の発生や人の死亡、病気の発症など、ランダム性が強い事象であっても、例外によってポアソン分布を利用できないケースがたくさんあることを理解しましょう。
期待値と発生頻度を利用し、ポアソン分布で確率を計算する
二項分布を利用するとき、一般的には正規分布へ近似します。ただ正規分布ではなく、ポアソン分布へ近似することもできます。正規分布とは違い、発生確率が低かったり、試行回数が多かったりする場合、ポアソン分布を利用できます。
ポアソン分布が優れているのは、試行回数を利用する必要がないことです。期待値(平均)と発生回数を利用すれば、発生確率を計算できます。
特定の範囲について、発生確率を知りたいときはポアソン分布を利用しましょう。ただ相関関係の強い事象が発生する場合、ポアソン分布を利用できなくなるデメリットも理解しましょう。
統計学で学ぶのがポアソン分布です。正規分布との違いやポアソン分布の特徴、使い分けをするときの考え方を理解し、確率の計算をするといいです。