中学数学で学ぶ分野の一つが円周角です。円を利用した角度が円周角であり、円周角の性質を利用することで角度を計算することができます。
円周角には性質があり、これを円周角の定理といいます。円周角の定理を理解していなければ角度を計算することができません。また円周角の定理を利用した応用問題も存在するため、円の中にある角度をどう計算するのか特殊な例を含めて学ぶ必要があります。
それでは、円周角の定理をどのように利用して計算問題を解けばいいのでしょうか。また、そもそも円周角とは何なのでしょうか。
中学数学の図形で学ぶ円周角の定理について、どのような内容になっているのか解説していきます。
もくじ
円周角とは何か?弧と中心角の意味
まず、円周角とは何でしょうか。円周角を理解する前に、弧と中心角について学ばなければいけません。円について、以下の部分が弧と中心角です。
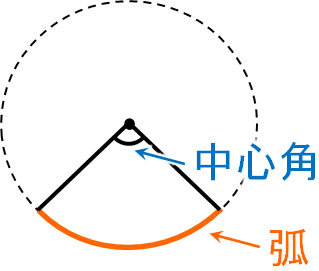
円周角の定理を利用するとき、弧と中心角を頻繁に利用します。そのため、どの部分が弧や中心角なのか把握しましょう。
一方で円周角は以下の部分を指します。
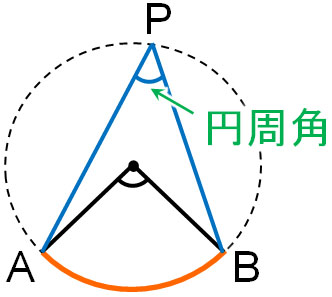
弧ABを数学では\(\stackrel{\huge\frown}{AB}\)と表します。\(\stackrel{\huge\frown}{AB}\)に対する∠APBを円周角といいます。円周角には必ず弧が存在します。また円周角が存在する場合、必ず中心角も存在します。
円周角の定理は2つある
それでは、円周角の定理には何があるのでしょうか。円周角には2つの性質があります。それぞれ以下になります。
- 中心角の半分が必ず円周角になる
- 弧の長さが同じ場合、必ず円周角は等しい
円周角の定理の内容を確認していきましょう。
中心角の半分が必ず円周角になる
円周角の定理では中心角が頻繁に利用されます。この理由として、円周角と中心角は以下の関係があるからです。
- 円周角 × 2 = 中心角
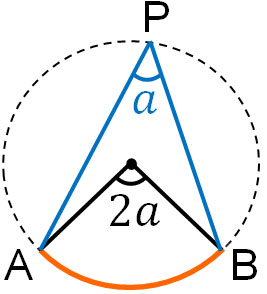
例えば円周角が30°の場合、中心角は必ず60°です。円周角を二倍すれば中心角の角度になります。一方で中心角が80°の場合、円周角は必ず40°です。中心角の半分が円周角の角度です。
弧の長さが同じ場合、必ず円周角は等しい
他にも円周角の定理があります。同じ円について、弧の長さが同じ場合は円周角が等しくなります。例えば以下の円周角はすべて同じ角度です。
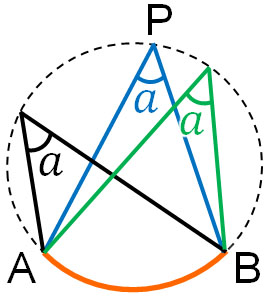
同じ弧を利用することによって、他の角度を出すことができます。例えば以下の図について、\(a\)の角度はいくらでしょうか。
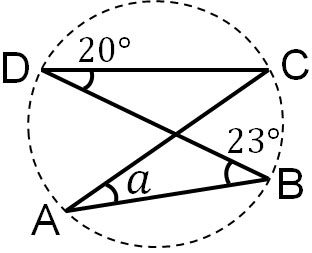
\(\stackrel{\huge\frown}{BC}\)に着目すると、∠BDCは20°です。そのため、\(a\)の角度は20°と分かります。
弧が半円の場合、円周角は90°になる
ここまで、円周角の定理で最も基本的なことを述べました。ただ、円周角の定理を利用する計算問題では、より複雑な問題が出題されます。そのため、応用問題を解けるようにしなければいけません。このとき頻繁に利用される内容として、弧が半円のケースがあります。
弧が半円の場合、以下のようになります。
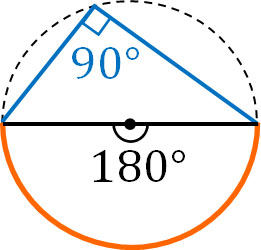
弧が半円だと中心角は180°です。そのため、円周角は必ず90°になります。以下のように、どの円周角であっても90°です。
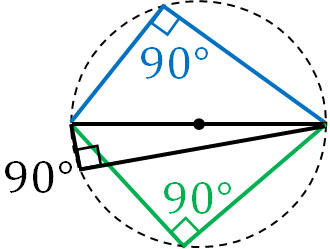
中心角が特殊な形になると、円周角の角度が分かりにくくなります。いずれにしても弧が半円の場合、円周角は必ず90°になると覚えておきましょう。
半円よりも大きい弧の円周角はどうなるのか
一方で半円よりも大きい弧の円周角はどのように考えればいいのでしょうか。弧の長さが小さいときがあれば、以下のように弧が長い場合もあります。
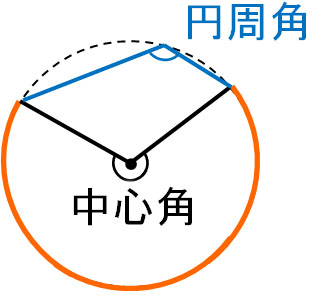
考え方はこれまで説明した内容と同じです。弧が半円よりも長い場合、中心角は180°以上になります。そのため、円周角は必ず90°以上になります。
弧の長さは必ずしも半円よりも短いとは限りません。今回のように、半円よりも長いケースがあります。その場合、どこが中心角であり、どこが円周角なのか理解するようにしましょう。例えば、以下のように中心角と円周角の関係を考えるのは間違いです。
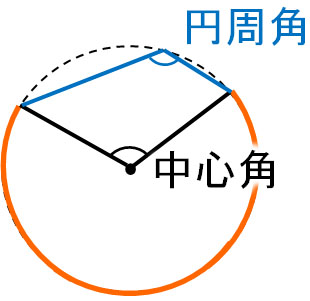
上図では、中心角は180°よりも小さいです。それにも関わらず、図をみる限り円周角は90°よりも大きいです。そのため、この関係での中心角と円周角は明らかに間違いと分かります。
中心角と円周角がどの場所にあるのか正確に把握しなければ正しく角度を計算することができません。特に弧が半円よりも長い場合、ミスが起こりやすいです。そこで中心角が180°よりも大きい場合、円周角が90°よりも大きくなっているかどうかを確認しましょう。
円に内接する四角形で対角の角度を足すと180°になる
ここまでの内容を学べば、円に内接する四角形の角度の性質を理解できるようになります。円に内接する四角形について、対角を足すと必ず180°になります。
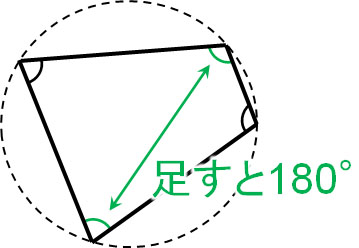
なぜ、2つの角度を足すと180°になるのでしょうか。この理由について、ここまで学んだ円周角の定理を利用して確認しましょう。
それぞれの角について、弧と中心角、円周角の関係は以下のようになります。
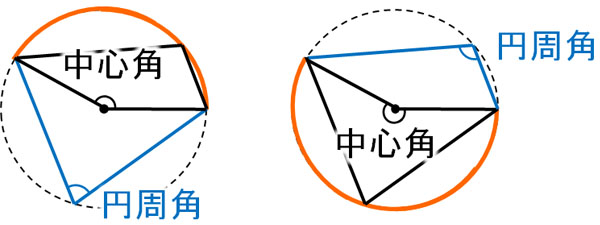
重要なのは、2つの中心角を足すと360°になることです。また円周角は中心角の半分です。そのため、2つの円周角(対角)を足すと180°になります。
円に内接する四角形について、対角を足すと180°になる性質を覚えておけば角度の計算で役立ちます。円に四角形が内接している必要はあるものの、対角を足すと必ず180°になることを覚えておきましょう。
弧の長さと円周角は比例する
また、同じ円について弧の長さと円周角は比例します。つまり弧の長さが2倍になれば、円周角も2倍になります。
中心角と弧の長さが比例することは理解しやすいです。以下のように、中心角が30°から60°に増えれば、弧の長さは2倍になります。

弧の長さは円周と中心角を利用して計算できます。例えば円の直径を\(b\)とするとき、中心角30°の弧の長さは以下のようになります。
- \(b×π×\displaystyle\frac{30°}{360°}\)
一方で中心角60°の弧の長さは以下になります。
- \(b×π×\displaystyle\frac{60°}{360°}\)
このように中心角が2倍になれば、弧の長さは2倍になります。同じように考えれば、円周角が2倍になれば、弧の長さは2倍になります。中心角と弧の長さは比例します。また、中心角と円周角は比例します。そのため、円周角と弧の長さは比例します。
同様に考えると、中心角または円周角が3倍になると、弧の長さは3倍になります。また弧の長さが4倍になると、中心角と円周角は4倍になります。弧の長さと円周角が比例することを理解しましょう。
練習問題:円周角の定理を利用して角度を計算する
Q1. 次の角度を求めましょう
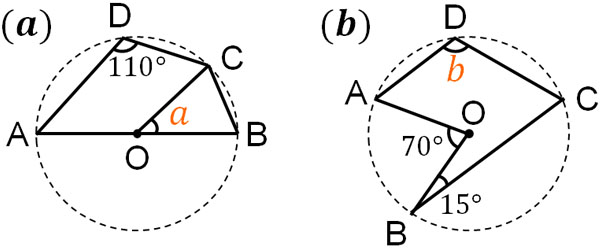
A1. 解答
角度を求める問題では、分かる角度をランダムに記入していきましょう。そうすれば、最終的に角度を出すことができます。
また角度の出し方は一つではなく、複数の方法があります。どの方法であっても、答えを導き出すことができれば問題ありません。
(a)
∠ADCに対応する弧は\(\stackrel{\huge\frown}{ABC}\)です。中心角は円周角の二倍なので、中心角は220°です。
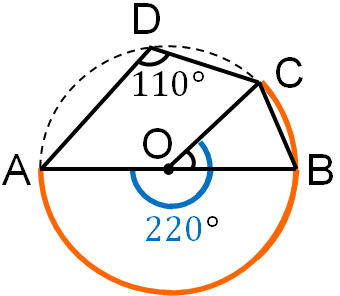
∠AOBは180°です。そのため、\(∠a\)は40°です。
- 220° - 180° = 40°
(b)
複雑な問題の場合、一部の天才を除いて答えをすぐに出すことはできません。そこで積極的に図に線を引き、角度を記入しましょう。そうすれば、最終的に答えを出せるようになります。
中心Oから線を引く場合、必ず長さは同じになります。つまり、二等辺三角形を作れます。二等辺三角形では底角が同じなので、以下のように角度を導き出すことができます。
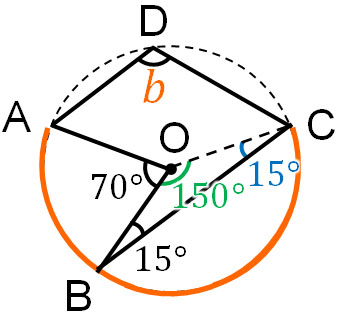
二等辺三角形なので、∠BCOは15°です。そのため、∠BOCは150°と分かります。一方で\(∠b\)に対する弧は\(\stackrel{\huge\frown}{ABC}\)です。\(∠b\)に対応する中心角は以下のようになります。
- 70°+150°=220°
中心角が220°なので、\(∠b\)は110°になります。
この答えを出すためには、前述の通りランダムに線と角度を図に記入していく必要があります。そうした中から、答えを出すために必要な角度を見つけ、計算をしていきましょう。
円周角の性質を利用して分からない角度を計算する
覚えるべき円周角の定理は2つです。一つは、中心角の半分が円周角になることです。もう一つは、弧の長さが同じ場合、必ず円周角は同じになります。
ただ、円周角の定理は2つだけであるものの、応用まで含めると理解しなければいけない内容は多いです。弧の形状が半円であったり、半円よりも長かったりする場合、円周角がどのようになるのか事前に把握しましょう。
また円に内接する四角形では、対角を足すと必ず180°になります。他には、弧の長さと円周角の大きさは比例します。
これらを利用して円周角の問題を解きましょう。円周角の問題は複雑になりやすいため、分かる角度をランダムに記入していくことで答えを導き出すといいです。