すべての人にとって小学算数は必須です。日々の生活で計算することは多く、割合や速度の計算などは全員が日常的に行います。
一方で中学数学や高校数学を学ぶ意味には何があるのでしょうか。平方根の計算を日常生活ですることはありません。また、二次関数や三次関数の計算をすることもありません。微分や積分となると、まず利用しません。それにも関わらず、私たちは難しい数学を学びます。
この理由として、多くの職業で数学を必要とすることが多いからです。つまり数学を理解していないと、あなたの将来の選択肢が非常に少なくなります。
なぜ数学を学ぶ必要があるかというと、あなたの未来の可能性が広がるからです。数学を学ぶことによって論理的思考が身につくかどうかはわからないものの、あなたが将来、活躍できるようになるのは間違いありません。この理由について解説していきます。
もくじ
世の中は物理や統計で成り立っている
私たちが住む世界は数学で成り立っています。数学で成り立つというのは、より正確にいうと物理や統計などで成り立っています。
大学で物理や統計を学ぶとわかりますが、中身はほぼ数学です。三角関数や微分・積分などを用いて、世の中の現象を説明するのが物理です。つまり数学ができないと、物理を理解することはできません。
また統計データを解析するとき、統計学を学ばなければいけません。このとき、当然ながら数学を理解していないとデータ解析することができません。
高校数学は航空や医療など、実世界で利用される
物理や統計が数学で成り立っていることを理解すると、中学・高校数学は世の中のあらゆる分野で利用されていることがわかります。
例えば物理であれば、航空や建築、機械・電機、測量など、あらゆる分野で数学が利用されます。
また統計であれば、工場や医療、保険、カジノなど多くの場面で利用されます。「工場で不良品が検出される確率」「新薬に効果があるかどうか統計処理する」「死亡確率から生命保険の商品内容を設計する」「カジノが儲かるようにシステムを組む」など、これらはすべて統計学が利用されています。

他には自ら起業してビジネスをする場合、どの方法であれば利益が増えるのか確認するため、統計データを取得して解析することは多いです。数学ができないとビジネス拡大を勘に頼るようになり、売り上げを作ることができないのです。
また会計や経済を学ぶときについても数学が利用されます。数学というのは、あらゆる専門分野で利用されます。
数学を極めると哲学に近くなる
先ほど説明した通り「数学≒物理」です。大学ではほぼすべての人が数学を学びます。また物理は当然として、統計や医療、会計、経済、金融は数学で成り立っています。分野は違うものの、これらの分野で活躍するためには数学を理解していないといけません。
一方、数学を極める必要はありません。大学で学ぶ数学というのは、中学・高校で学ぶような数学とは大きく異なり、哲学に近くなるからです。数学が哲学とは、どういう意味なのでしょうか。
例えば、自然数を考えてみましょう。1、2、3……のような正の整数を自然数といいます。自然数には隣に数があります。3の隣にある自然数は2と4です。
一方、小数(分数)の隣にある数は何でしょうか。例えば、0.5の隣にある数字は何でしょうか。0.5の隣にある数は0.4や0.6ではありません。0.49や0.51のほうが、0.5の近くにあります。また0.49よりも、0.499のほうが0.5に近いです。
このように考えると、隣にある数を特定できないことがわかります。この性質を稠密性(ちょうみつせい)と呼び、イメージとしてはぎっしり詰まっている様子です。ただどれだけ小さい数を考えたとしても、隣にある数字はわかりません。
「隣にある数字は何か?」という問いについて、答えるのは簡単そうに思えるものの、実は答えがありません。こうした問題を自ら設定し、証明したり計算したりするのが大学の数学です。
数学を極める人では、「数とは何か」を考えます。このような事実を理解すると、なぜ大学課程の数学が哲学に似ているのか理解できると思います。
中学・高校過程の数学というのは、既に知られている公式を利用して問題を解き、答えを出すのが目的です。そのため中学・高校数学は物理や統計、会計、経済など多くの場面で利用されるのです。
一方で数学学者を除いて、数学を極める必要はありません。ただ数学を利用できるようになるのは優れています。数学を利用して問題を解くことができれば、あらゆる分野で活躍できるようになるからです。
一般人でも数学が必要になることは多い
なお実際のところ、専門職でないにしても、一般人で数学が必要になることは非常に多いです。例えば資格試験を受けるとき、多くの場面で数学の問題が出されます。
物理や統計が関わる資格であれば、数学が関わるのは当然です。ただこうした分野でなくても、公務員試験や会計試験など多くの場面で数学が関わる問題が出されます。
例えば私の場合、日本で薬剤師資格を保有しています。日本の薬剤師国家試験では、医薬品の体内での分解速度を計算したり、薬の溶出度合いを計算したりしなければいけません。つまり数学ができない場合、試験に合格することができません。
より身近な例でいえば、最安値で旅行するときすべての人が数学を利用します。バスや電車など複数の移動方法がある中で、どの方法を利用すれば安い金額にて、最短で目的地に到着できるのか考えなければいけません。
このとき、多くの人が無意識に関数を利用して計算しています。実際に関数の問題を解くことはないものの、頭の中で計算することによって、おおよその答えを導き出すのです。

他には、投資をするときに将来の資産がいくらになるのか計算するときに数学を利用します。
正しく投資をすれば年利8~10%は簡単であり、最もリスクの低い投資であっても年利4%は誰でも達成できます。例えばS&P500(アメリカのトップ500社に投資をするインデックス)では、「配当を含めて年利8~10%になる」と広く知られています。
それでは、年利8%で投資をすれば将来の資産はどのようになるでしょうか。この計算をするときは累乗を使います。以下のようになります。
- 10年後:\((1.08)^{10}≒2.15\)倍
- 20年後:\((1.08)^{20}≒4.66\)倍
- 30年後:\((1.08)^{30}≒10.06\)倍
- 40年後:\((1.08)^{40}≒21.72\)倍
このように、時間経過とともに資産が大幅に上昇していきます。なぜお金持ちがずっとお金持ちなのかというと、彼らは資産のほとんどを投資しており、時間が経てば勝手に資産が増えるようになっているからです。
また使うお金よりも、お金が増えるスピードのほうが速いため、彼らの資産が減ることはありません。むしろ、時間経過と共に金持ちの資産は増えていきます。
なぜ富裕層が全員、投資をしているのかは数学を学ぶことで理解できます。お金持ちだから投資をしているのではありません。投資をしているため、結果としてずっと富裕層なのです。数学を学べばこの事実を理解でき、積極的に投資しなければいけないとわかります。
数学で論理的思考が身につくかどうかはわからない
なお、数学を学ぶ目的として「論理的思考を身に付けることができるから」という理由も広くいわれています。ただ私の個人的な意見としては、数学を学ぶことによって論理的思考が身に付くかどうかはわかりません。中学・高校で学ぶ数学というのは、暗記できるかどうかが重要だからです。
中学・高校での数学というのは、既に知られている公式を利用して問題を解きます。また解き方のパターンが決まっています。「この問題ではこの公式を利用する」と決まっており、解き方を覚えるのが数学です。
つまり中学や高校の数学では、問題をみて「解き方の候補を思いつけるかどうか」が重要になります。問題の解き方を覚えておらず、解き方の候補を思いつけない場合、答えを得ることはできません。
例えば以下の問題について、\(x\)には何が当てはまるでしょうか。
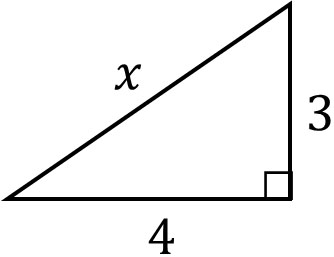
三平方の定理を習っている人であれば、答えは5とすぐにわかります。ただ三平方の定理を学んでいない場合、この問題を解くことはできません。問題を解けるのは「直角三角形では三平方の定理を利用できる」と理解しており、問題の解き方を知っているからなのです。
こうした定理を発見するためには、新たな発想や論理的思考が必要になるかもしれません。ただ中学・高校数学で問題を解くとき、重要なのは解き方を知っているかどうかであり、論理的思考ではないのです。
数学が得意な人であっても、論理的思考ができず、儲け話に騙されて詐欺被害に遭う人は多いです。また数学が得意な人であっても、宝くじに当たった後に投資にお金を回さず散財してしまい、結果的に破産してしまう人は多いです。
数学の問題が解けるのと、論理的思考ができるのは別問題です。論理的思考を鍛えるためには、ほかの人にプレゼンテーションをしたり、新たな事業を立ち上げたり、人生経験の中で養っていく必要があります。
高度な数学はあなたの可能性を広げる
ただいずれにしても、中学・高校数学を勉強することは将来あなたの可能性を大きく広げることにつながります。
働くことなく、投資をすることもなく、日々を漫然と過ごすだけの人生を歩む場合、確かに数学を勉強する意味はないかもしれません。一方、ほとんどの人は数学が必要になります。すべての人が仕事で計算を利用するからです。
また専門職の場合、ほぼ確実に高度な数学を利用します。こうした人たちは給料が高く、さらには起業した場合においても、ほかの人がそのビジネスを真似しにくいので成功しやすいです。
また数学が必要ないと思われる職業であっても、数学がわかると簡単に利益を作ることができます。例えば製薬企業の営業マンは医師に対して薬を売ります。薬が効くかどうかは、前述の通り統計学を利用します。また、体内での薬の挙動は数学を利用して計算します。
そのためこれらのデータを数学で説明できる場合、医師に対して優れたプレゼンができるようになります。
ほかにはファイナンシャルプランナーであれば、「どのような資産形成をすれば将来の資産を作り、老後に備えられるのか」についてお客さんにアドバイスする必要があります。そのためには、金融商品の知識に加えて数学が必要です。保険や住宅ローンというのは、統計や経済で成り立っているからです。
実際のところ、営業職やコンサルタントで数学を利用している人は少ないです。そのため数学を使えれば、簡単に他の営業マンと差別化できて利益を作ることができます。
数学の問題を解くことができても、論理的思考が身につくかどうかは不明です。ただ数学を学べば、あなたの将来性が非常に優れることは間違いありません。
数学は多くの場面で利用されている
多くの分野で数学が利用されています。物理や統計は数学で成り立っており、計算することによって答えを得ることができます。
ただ、数学の問題を解けること自体に価値はありません。数学は世の中の現象を説明するためのツールです。そのため、ツールを利用できることが重要です。ツールを利用することによって、「工場の生産効率を改善できているか」「効果的なマーケティングができているか」などを検証することができます。
つまり数学というのは、実世界に役立てることができる場面が多いため、私たちは学ぶというわけです。中学・高校数学では難解な問題を解くだけであるため、何の役に立つのか不明です。ただ実際には、ビジネスや投資を含めてあらゆる分野で数学が利用されています。
数学を学べば、世の中の現象や経済がわかります。例えば、なぜ金持ちがずっと金持ちなのかは、数学を学べばわかります。数学の問題を解くことができても、豊かになれるかどうかはわかりません。ただ豊かな生活を送っている人は、全員が数学を日常的に利用している事実を理解しましょう。






