電気と磁気には密接な関係があります。電流が流れている場合、磁力(磁気力)を生じるのです。磁場あると力が発生するため、力の大きさを理解しなければいけません。
なお電流によって磁力を生じているため、電流の強さによって発生する力の大きさは異なります。また、導線の形によって発生する力が変化します。そこで、公式を利用することによって力の大きさを計算できるようになりましょう。
また磁場には向きがあります。電流が流れている方向に対して、特定の向きに磁場が発生するのです。磁場が発生する向きを見つける方法として右ねじの法則があります。この法則を利用して、電流と磁場の向きを確認しましょう。
それでは、磁場の性質には何があるのでしょうか。また、電流によって発生する磁場にはどのような公式があるのでしょうか。磁場が発生するときの力の計算方法を解説していきます。
もくじ
磁場と磁力、磁気量、磁気線の関係
多くの人が磁石を利用して遊んだことがあると思います。磁石の周辺には磁場があります。目に見えない場合であっても、場が存在する場合は力が働きます。あなたが物体に触れていなくても、重力があると物体に力が加わり、下に落ちます。同様に、磁場があると物体に力が加わるのです。
磁場はN極からS極に向けて発せられます。正の電荷から負の電荷に向けて電場が発せられるのと同じように、磁場も特定の向きで発生します。このとき磁場の向きを可視化した線を磁力線といいます。

このとき、N極とN極(またはS極とS極)では互いに反発します。一方でN極とS極を近づけると互いに引き合います。このような力を磁力(磁気力)といいます。磁場が存在する場合、物体に触れていなくても磁力によって力が発生するのです。
なお磁石によって磁極(N極とS極)の強さが異なります。磁極の大きさを磁気量と呼び、単位はWb(ウェーバ)です。なお磁気量が\(m_1\)[Wb]、\(m_2\)[Wb]の磁極が\(r\)[m]離れている場合、磁力の大きさ\(F\)には以下の関係があります。
- \(F=k_m\displaystyle\frac{m_1m_2}{r^2}\)
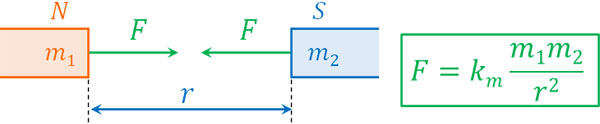
※\(k_m\)は比例定数
このように、静電気力(クーロン力)を得る公式と同じです。磁場と電場では、同じ法則がいくつもあります。なお、磁力の大きさを得る先ほどの公式は重要ではないため、覚える必要はありません。
参考までに、磁場\(H\)[N/Wb]が発生している場所に磁気量\(m\)[Wb]の磁極を置く場合、磁極が受ける力\(F\)は以下のようになります。
- \(F=mH\)
電場では、\(F=qE\)を公式として利用します。この公式に相当するのが\(F=mH\)です。なお、この公式も重要ではないので覚える必要はありません。
また、磁気量の単位であるWb(ウェーバ)についても利用する場面はほとんどありません。そのため磁気量とWbについても、そこまで重要ではありません。
電流\(I\)が流れると磁場\(H\)が作られる:右ねじの法則
磁場の概要を学んだら、電流が流れることによって作られる磁場の大きさ\(H\)を計算できるようになりましょう。また、磁場の向きを把握できるようになりましょう。
1820年、デンマークの物理学者であるエルステッドは「導線に電流を流すことにより、その周辺に磁場が発生する」ことを発見しました。以下のように、電流を中心として同心円状に磁力線が並びます。
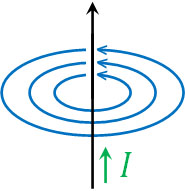
電流と磁場の向きを把握するとき、右ねじの法則を利用しましょう。右手を利用し、「Good(いいね)」の形を作ります。このとき、親指とその他の指(4本の指)の向きの関係は、電流\(I\)と磁場\(H\)の向きと同じになります。これを右ねじの法則といいます。
具体的には、右ねじの法則では以下のようになります。
- 親指の向きに電流\(I\)が流れている → その他の指の向きが磁場\(H\)の向き
- その他の指の向きに電流\(I\)が流れている → 親指の向きが磁場\(H\)の向き

このように、親指を電流\(I\)の向きと仮定する場合、その他の指(人差し指、中指、薬指、小指)の向きが磁場\(H\)の向きになります。一方で親指を磁場\(H\)の向きと仮定する場合、その他の指の向きが電流\(I\)の向きになります。
電流と磁場の向きを知りたい場合、右手でGoodの形を作りましょう。これにより、あらゆるケースで電流と磁場の向きがわかります。
なお前述の通り、電流が流れると磁場が作られます。このとき、以下の3パターンに分けて磁場の強さを考えましょう。
- 直流電流が作る磁場
- 円形電流が作る磁場
- ソレノイドが作る磁場
これらは状況が違っており、磁場の強さを得る公式も異なります。そこで、それぞれの状況について公式を含めて解説していきます。
直流電流が作る磁場の公式
電線がまっすぐ伸びているとき、電流を流すと、当然ながら電流はまっすぐ進みます。この場合、磁場の強さ\(H\)[A/m]は電流の大きさ\(I\)[A]に比例し、電流(導線)からの距離\(r\)[m]に反比例します。このとき、以下の公式によって直流電流が作る磁場の大きさ\(H\)を得ることができます。
- \(H=\displaystyle\frac{I}{2πr}\)
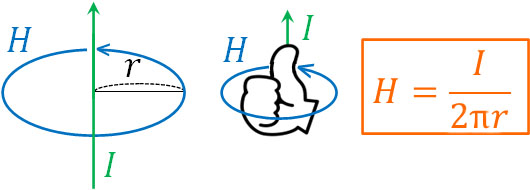
電流が強くなると磁場が強くなるのは感覚的にも理解できます。また、電流からの距離が遠くなると、磁場が弱くなることも理解できます。そのため、このような公式となるのです。
それでは、この公式は何を意味しているのでしょうか。先ほどの公式を以下のように変形しましょう。
- \(I=2πr×H\)
電流(導線)から距離\(r\)の場所にある点について、発生している磁場は磁場\(H\)です。ただ先ほどの図の通り、磁場は円形です。そこで、特定の点だけではなく、円周(\(2πr\))に沿って磁場\(H\)をすべて足しましょう。
そのため、かけ算をして\(2πr×H\)となります。これによって得られるのが電流\(I\)というわけです。
なお先ほど、磁場の単位としてN/Wbを記しました。ただ先ほどの公式をみてわかる通り、分子に\(I\)、分母に\(r\)があるため、磁場の単位はA/mでもあります。
参考までに、磁場の単位でN/Wbが利用されることはほとんどなく、主にA/mが利用されます。Wb(ウェーバ)は単位として利用する場面がほとんどないため、重要ではないのです。
円形電流が作る磁場の公式
なお、導線がまっすぐの形状とは限りません。導線が円の形状となっており、電流が円形にて流れるケースもあります。その場合についても、右ねじの法則を利用することで電流と磁場の向きを確認しましょう。
円形電流が作る磁場については、先ほどの公式とは異なります。電流の大きさが\(I\)であり、電流(導線)が作る円の半径が\(r\)[m]のとき、作られる磁場の大きさ\(H\)[A/m]は以下のようになります。
- \(H=\displaystyle\frac{I}{2r}\)
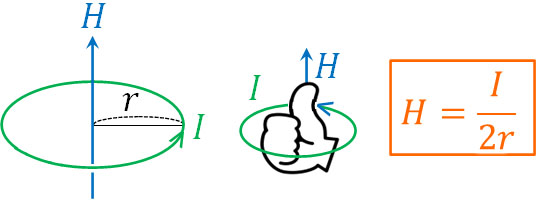
注意点として、この公式で得られる磁場\(H\)というのは、円の中心に作られる磁場の大きさを表します。実際には、磁場はさまざまな場所に作られます。そうした磁場の中でも、円の中心に存在する磁場\(H\)を計算するときに先ほどの公式を利用するのです。
また直流電流が作る磁場とは異なり、円形電流が作る磁場では、公式の分母に\(π\)がありません。それぞれの公式を区別し、間違えて利用しないようにしましょう。
導線が\(N\)巻されている場合の磁場
先ほど記した円形電流が作る磁場の公式というのは、導線によって一つの円が作られている場合に得られる磁場の強さです。それでは一つの円ではなく、導線によって複数の円が作られている場合はどのように考えればいいのでしょうか。つまり導線が\(N\)回、巻かれている場面を考えましょう。
計算方法は簡単であり、\(N\)をかけましょう。一つの円では、円の中心に作られる磁場は\(H=\displaystyle\frac{I}{2r}\)です。そのため導線が\(N\)巻されている場合、円の中心に作られる磁場は以下のようになります。
- \(H=N\displaystyle\frac{I}{2r}\)
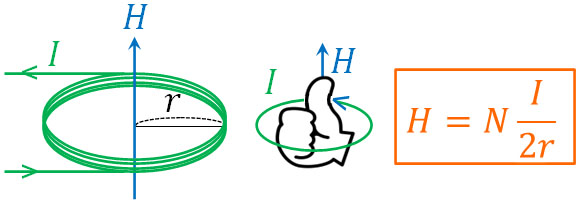
こうして、電流によって作られる磁場の大きさを計算できます。
ソレノイドが作る磁場の公式
次に、ソレノイドが作る磁場を計算できるようになりましょう。ソレノイドとは、以下のように、円筒状に導線を巻いた形状を指します。ソレノイドについても、右ねじの法則によって電流と磁場の向きを把握できます。
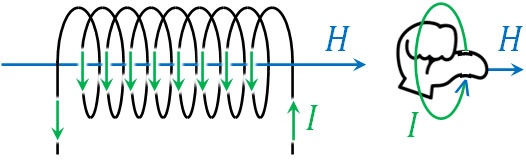
それでは、ソレノイドが作る磁場の大きさはどのように計算すればいいのでしょうか。1mあたりの導線の巻数が\(n\)回の場合、以下の公式によって磁場\(H\)を計算できます。
- \(H=nI\)
なお、\(n\)は先ほど記した\(N\)とは異なります。\(N\)は巻数のことであり、例えば100回巻きであれば、\(N=100\)です。
一方、\(n\)は1mあたりの巻数です。そのため巻数が100回であっても、0.5mで100巻きであれば、\(n=200\)になります。
電流と磁場に関する練習問題
ここまで学んだことを利用して、電流と磁場に関する練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 同じ平面上に、まっすぐの形状である導線Aと半径\(r\)の円形導線Bがあります。導線Aと円形導線Bの中心との距離が\(3r\)であり、円形導線Bでは反時計回りに電流\(I\)が流れています。導線Aに電流を流すと、円形導線Bの中心Oで磁場が消えました。導線Aを流れる電流の大きさと向きを求めましょう。
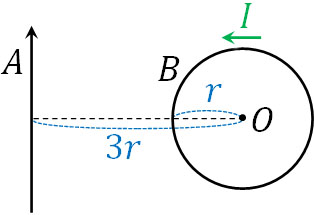
点Oでの磁場がゼロというのは、電流Aによる磁場と電流Bによる磁場が打ち消し合い、結果として磁場が消えることを意味します。そこで導線Aによる電流を\(I_A\)とすると、以下の式を作ることができます。
\(\displaystyle\frac{I_A}{2π·3r}=\displaystyle\frac{I}{2r}\)
\(I_A=3πI\)
こうして、電流Aの大きさは\(I_A=3πI\)とわかりました。次に、磁場の向きを確認しましょう。導線Aと導線Bは同一平面上にあります。そこで導線Aと導線Bが机の上にあると仮定して、あなたの右手を利用して磁場の向きを確認しましょう。
机の上に置かれている円(導線)対して、反時計回りに電流が流れている場合、手は以下のような形になります。
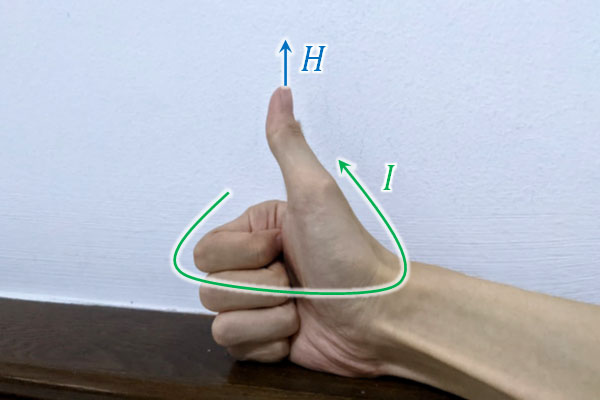
つまり、磁場の向きは上(天井)になります。そこで磁場を打ち消すためには、下(地面)の向きに磁場が発生すればいいとわかります。
なお、机に置かれている直線の導線が下向きに磁場を発するためには、電流の向きが以下の写真と同じであればいいとわかります。
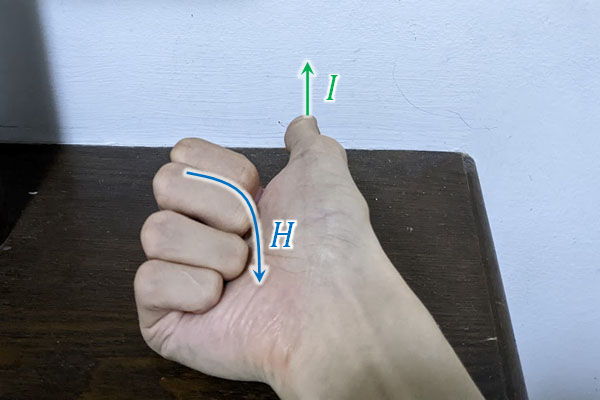
先ほどの図では、以下の向きに電流\(I_A\)が流れると電場が打ち消し合うことになります。
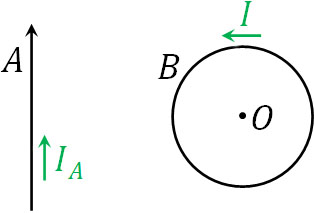
磁場の問題を解くとき、二次元ではなく三次元で考えなければいけません。そのため向きを知りたい場合、必ずあなたの右手を利用して方向を確認しましょう。これにより、電流や磁場の向きがわかるようになります。
磁場の強さと向きを把握する
すべての人が磁石を使ったことがあります。磁場が存在する場合、磁力を生じます。磁力により、反発または引き合う力を生じるのです。
なお電気と磁気は密接な関係があります。電磁気学で磁場を学ぶのは、電気に対して公式や性質が似ているからなのです。
磁場の向きを知りたい場合、右ねじの法則を利用しましょう。あなたの右手を利用することにより、磁場の向きがわかります。磁場は三次元であるため、実際に右手を利用しないと電流や磁場の向きを知ることはできません。
また磁場の強さを得る公式は3つあります。直流電流が作る磁場、円形電流が作る磁場、ソレノイドが作る磁場とそれぞれ公式が違います。そこで、それぞれの公式を使い分けて磁場の計算を行いましょう。






