物理で力学を学ぶとき、最も重要な内容の一つが運動方程式(ニュートンの第二法則)です。運動方程式を利用することにより、力の向きや加速度の大きさがわかるのです。
運動方程式を学ぶとき、力がつり合っている状態(加速度のない状態)と運動方程式を作れる状態(加速度がある状態)の違いを理解しましょう。また、運動方程式は複数の力を合算させることで得られる事実を学ぶことも重要です。
運動方程式の概要を理解したら、さまざまなパターンで練習問題を解きましょう。物体が一体化するケースや糸・ばねを利用するケース、定滑車・動滑車を使うケースなど、実際に練習問題を解くことによって運動方程式の作り方を学ぶのです。
それでは、運動方程式とは何でしょうか。また、どのように運動方程式を作ればいいのでしょうか。力学で重要な運動方程式の作り方を解説していきます。
もくじ
質量と加速度をかけることで力を得られる
まず、運動方程式(ニュートンの第二法則)とは何かを学びましょう。運動方程式とは、一つの物体に対して成り立つ関係式を指します。すべての教科書では、以下のように運動方程式を定義しています。
- \( \overrightarrow{F} =m \overrightarrow{a} \)

※\(\overrightarrow{F}\)は力の大きさ、\(m\)は物体の質量、\(\overrightarrow{a}\)は加わっている加速度です。
ただこの式を覚える必要はなく、あなたは既に理解しています。力の大きさ\(F\)の単位はニュートン(N)です。力の大きさを計算するとき、質量\(m\)と加速度\(a\)をかけることを習っていると思います。事実、重力は質量\(m\)と重力加速度\(g\)のかけ算によって得られます。
\(F=ma\)と異なるのは、\( \overrightarrow{F} =m \overrightarrow{a} \)のように、矢印が記載されていることです。物理では、矢印はベクトルを表します。そのため運動方程式ではベクトル(力の向き)が重要になります。具体的には、運動方程式では力の向きと加速度の向きが一致している必要があります。
運動方程式と力のつり合いの違い
運動方程式を学ぶとき、多くの人が混乱する内容として「運動方程式と力のつり合いの違い」があります。力のつり合いでは、一つの物体に着目します。このとき、すべての力を足すとゼロになります。
運動方程式についても、一つの物体に着目します。ただすべての力を足してもゼロにはなりません。特定の方向に力が加わることにより、物体は加速します。
・加速(または減速)している物体には力が加わっている
重要なのは、物体が動いていても力が加わっていないケースが多い事実です。
静止している物体では、当然ながら力がつり合っています。ただ摩擦力のない地面で物体を滑らせる場合についても、物体は動いているにも関わらず、物体には何も力が加わっていません。つまり、力がつり合っています。
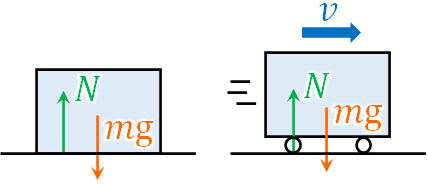
上図では、物体が静止している状態であっても、物体が速度\(v\)で動いている状態であっても、物体に力は加わっていません。そのため、図に記入できる力の種類や大きさは同じです。
等速直線運動では力は加わっておらず、力はつり合っています。一方で動いている物体(または静止している物体)に対して正の加速度を加える場合、物体は加速していきます。また負の加速度を加える場合、物体は減速または後退します。
物体が動いているかどうかで力のつり合いや加速度の有無を判断してはいけません。そうではなく、物体が加速または減速しているかどうかを確認しましょう。
力の合算(ベクトルの足し算)で力の方向がわかる
なお運動方程式では、重要な考え方がいくつかあります。一つは先ほど述べた通り、力のベクトル(力の向き)と加速度のベクトル(加速度の向き)が同じになっていることです。そのためベクトルの向きが異なる場合、角度(\(sinθ\)または\(cosθ\))を利用してベクトルを一致させなければいけません。
他に重要な概念として、「運動方程式によって最終的に得られる力の大きさは複数の力の足し算によって得られる」ことです。
例えば力の強いAさんと力の弱いBさんが異なる力で下図のように箱を押しているとします(床による摩擦力は無視します)。
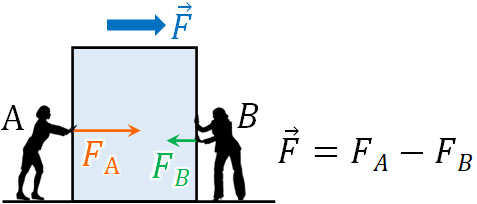
この場合、Aさんのほうが力は強いため、Aさんによる力からBさんによる力を引き、力の向きは右側に加わります。つまり、箱は加速度を伴って右側に進んでいきます。またAさんによる力とBさんによる力は同じ向き(Bさんの力は負なので反対向き)であるため、ベクトルの足し算が可能です。
次に、摩擦力のある床で箱を滑らせる場面を考えましょう。右向きに力を加える場合、作用・反作用の法則によって左向きに摩擦力が加わります。
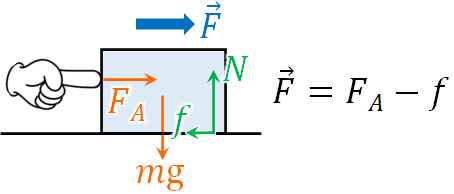
そのため、力の大きさは「右向きの力に対して、摩擦力を引く」ことによって得られます。このように運動方程式よって得られる力(加速度)というのは、すべての力を合算させることで計算できると理解しましょう。
運動方程式(ニュートンの第二法則)の作り方
それでは、実際に運動方程式(ニュートンの第二法則)を作ってみましょう。運動方程式を作る手順は以下になります。
- 着目物体を決め、着目物体に働く力を図に記入する
- 物体の運動方向と垂直方法に力を分解する
- 正の向きを決め、力を合算させることで\(\overrightarrow{F}\)を求める
例として、以下のように箱に糸をつけ、常に張力Tとなるように物体を斜め上方向に引っ張る場面を考えましょう(摩擦力は無視します)。
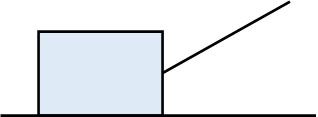
着目物体は箱であり、箱と触れている部分(糸と床)に対して力を加えましょう。また、重力を図に記載することで箱に働くすべての力を記入できます。
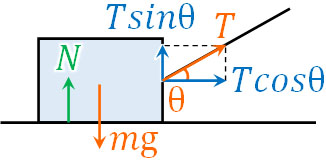
糸を引っ張る方向は右上です。ただ物体が右上に移動することはなく、地面と平行に右へ移動します。そこで、上図のように角度を利用して張力\(T\)を分解しましょう。
上図の場合、物体が移動する向き(水平方向)に加わっている力は\(Tcosθ\)のみです。そのため、\(F=Tcosθ\)です。また質量は\(m\)であるため、加速度\(a\)を利用することで以下の運動方程式を作れます。
\(Tcosθ=ma\)
\(a=\displaystyle\frac{Tcosθ}{m}\)
こうして、加速度\(a\)は\(\displaystyle\frac{T·cosθ}{m}\)と計算できます。
・なめらかな床の場合、摩擦力はゼロ
なお運動方程式を作るとき、摩擦力が働くかどうかを確認しましょう。なめらかな床に物体を置く場合、摩擦力はゼロです。しかしなめらかな床ではない場合、摩擦力を考慮して計算する必要があります。
運動方程式を利用する練習問題
ここまで解説した内容を理解して、運動方程式を作ることで計算問題を解きましょう。運動方程式を作り、答えを得られるようになるためには、何度も練習問題を解くのが最も効果的な方法です。
それでは、以下の問題の答えは何でしょうか。
- 地面との角度がθであるなめらかな斜面上に質量\(m\)の物体Aを置きます。物体Aを糸でつなぎ、滑車を利用して下図のように質量\(M\)の物体Bと糸をつなぎます。物体Bが鉛直下向きで動くとき、2つの物体の加速度\(a\)を求めましょう。なお、重力加速度\(g\)はです。
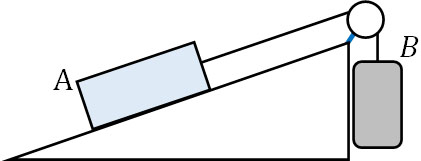
運動方程式を作るため、物体Aと物体Bに着目し、それぞれで力を図に加えましょう。以下のようになります。
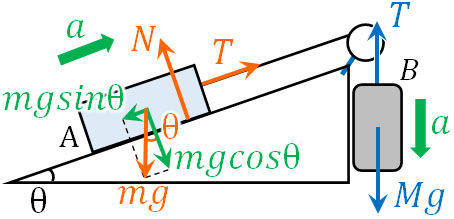
物体Aと物体Bが静止している場合、力がつり合っているため、同じベクトルの力を足して0になるように式を作ればいいです。
ただ運動方程式では、物体に力が加わることによって加速度が発生しています。そこで、物体Aに加わる力\(F_A=ma\)と物体Bに加わる力\(F_B=ma\)について、それぞれ運動方程式を作りましょう。前述の通り、物体の運動方向と同じ向きの力を合算させると、運動方向の力を得られます。
- 物体Aの力(斜面方向):\(ma=T-mg·sinθ\)
- 物体Bの力(斜面方向):\(Ma=Mg-T\)
こうして、2つの物体についてそれぞれ運動方程式を作ることができました。なお2つの物体の加速度は同じであるため、2つの運動方程式を利用して加速度\(a\)を計算しましょう。
\(Ma=Mg-T\)
\(T=Mg-Ma\)
\(T=Mg-Ma\)を\(ma=T-mg·sinθ\)へ代入する。
\(ma=Mg-Ma-mg·sinθ\)
\(a(m+M)=(M-m·sinθ)g\)
\(a=\displaystyle\frac{(M-m·sinθ)g}{m+M}\)
こうして運動方程式を作ることにより、\(a=\displaystyle\frac{(M-m·sinθ)g}{m+M}\)と計算できました。
2つの物体が一体化している場合、作用・反作用の法則が働く
先ほどは非常に単純なケースの練習問題を解きました。ただ運動方程式では、より複雑な問題を解かなければいけません。その一つに、2つの物体が一体化しているケースがあります。
例えば、以下の問題の答えは何でしょうか。
- なめらかな床で質量\(m\)の物体と質量\(M\)の物体をくっつけ、力\(F\)を常に加えます。2つの物体の加速度\(a\)を求めましょう。
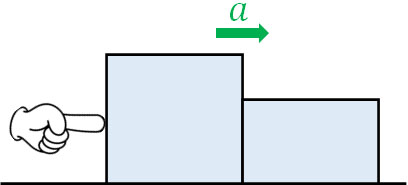
2つの物体はくっついているため、物体は一方の物体を押しています。それと同時に、作用・反作用の法則によって、押されている物体も反対方向の力で押すことになります。
物体が一方の物体を押す力を\(f\)としましょう。その場合、それぞれの物体について力の働きを図に記入すると以下のようになります。
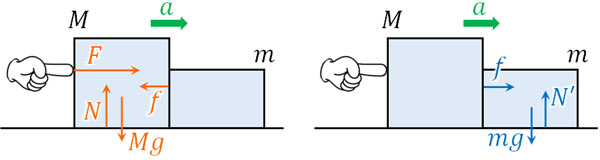
作用・反作用の法則により、「物体Mが物体mを押す力\(f\)」と「物体mが物体Mを押す力\(f\)」は同じです。そこで、それぞれの物体の運動方程式を作ると以下のようになります。
- 物体Mに着目:\(Ma=F-f\)
- 物体mに着目:\(ma=f\)
そこで、\(Ma=F-f\)に\(ma=f\)を代入しましょう。
\(Ma=F-f\)
\(Ma=F-ma\)
\(F=(M+m)a\)
\(F=(M+m)a\)となることからわかる通り、「物体がくっついているとき、力\(F\)は2つの物体の質量を足した後に加速度をかければいい」とわかります。言い換えると、くっついている2つの物体を1つの物体とみなして運動方程式を作ることができます。
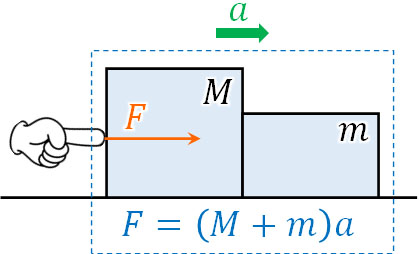
通常、異なる物体は別々に運動方程式を作らなければいけません。ただ一体化している物体の場合、例外的に質量を足すことで同じ物質とみなし、運動方程式を作ることができます。
糸やばねを利用するときの運動方程式
次に、糸やばねを利用する場合の運動方程式の立て方を学びましょう。糸やばねを利用して2つの物体をつなぐ場合、必ず糸の張力\(T\)は同じになります。また、必ずばねの弾性力\(kx\)は同じになります。
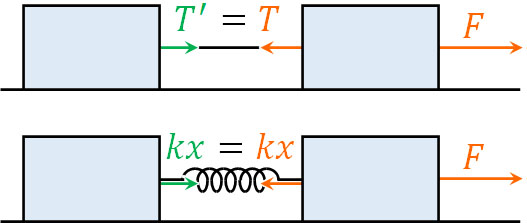
2つの物体に働く糸の張力は\(T’=T\)となりますし、2つの物体に働くばねの弾性力は両方とも\(kx\)となります。
糸やばねの質量を無視できる場合、張力や弾性力は同じであるため、力は互いに打ち消し合うことでゼロになります。つまり、2つの物体がくっついている状態と同じです。そのため、以下の図を描くことができます。
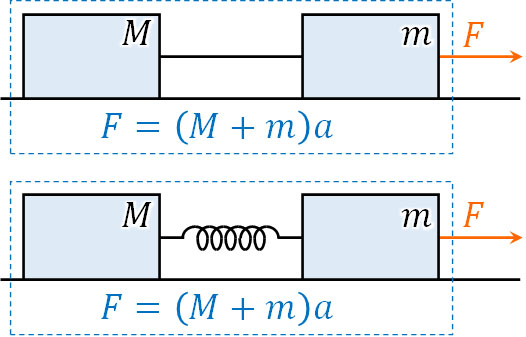
2つの物体の質量がそれぞれMとmの場合、運動方程式は\(F=(M+m)a\)となります。物体の間に糸やばねがあっても、無視できるのです。
定滑車と動滑車の性質:滑車に働く力
運動方程式では滑車を利用する問題もひんぱんに出されます。滑車には種類があり、定滑車と動滑車があります。運動方程式を作るとき、定滑車と動滑車の特徴を事前に学ばなければいけません。
位置が固定されている滑車が定滑車です。定滑車を利用する場合、力の大きさは同じです。また物体を1m引き上げる場合、あなたが引っ張らなければいけないひもの長さは1mです。
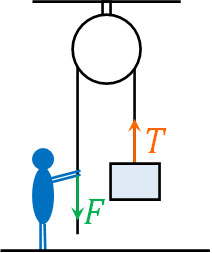
それに対して動滑車は動くことができます。動滑車を利用する場合、天井が半分の重さを支えているため、あなたが動滑車に加えるべき力は半分で済みます。ただし動滑車は動くため、例えば物体を1m上昇させるためには、あなたは2mを引っ張らなければいけません。
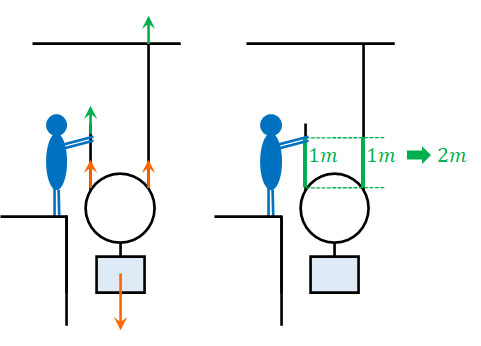
このように定滑車と動滑車では、必要な力や引っ張る距離に違いがあることを覚えましょう。
| 定滑車 | 動滑車 | |
| 力の大きさ | 変わらない | \(\displaystyle\frac{1}{2}\)倍 |
| 引っ張る距離 | 変わらない | 2倍 |
この違いを知っていないと、物理で滑車を含む問題を解くことができません。そのため、必ず定滑車と動滑車の違いを理解する必要があります。それでは、以下の問題の答えは何でしょうか。
- 摩擦がなく、重さを無視できる滑車を利用し、質量\(m\)と質量\(M\)の重りを下図のようにつるします。なお\(M>2m\)であり、重力加速度は\(g\)です。
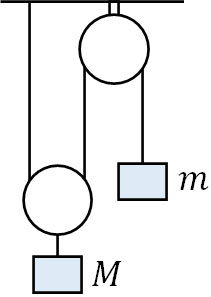
- 物体Mの加速度\(a_M\)と物体mの加速度\(a_m\)の関係を記しましょう。
- 物体Mと物体mの加速度を求めましょう。
1) 物体Mの加速度\(a_M\)と物体mの加速度\(a_m\)の関係を記しましょう
物体Mが距離\(x\)を動く場合、物体mは距離\(2x\)を動きます。動滑車を動かすためには、前述の通りその2倍のひもを動かす必要があるからです。そのため、等加速度直線運動の公式を利用すると以下のようになります(初速度\(v_0=0\))。
- 物体M:\(x=\displaystyle\frac{1}{2}a_Mt^2\)
- 物体m:\(2x=\displaystyle\frac{1}{2}a_mt^2\)
そこで、\(x=\displaystyle\frac{1}{2}a_Mt^2\)を\(2x=\displaystyle\frac{1}{2}a_mt^2\)へ代入しましょう。
\(a_Mt^2=\displaystyle\frac{1}{2}a_mt^2\)
\(2a_M=a_m\)
こうして、\(2a_M=a_m\)になるとわかります。つまり加速度\(a_M\)を2倍すると、加速度\(a_m\)を得られます。
2) 物体Mと物体mの加速度を求めましょう
\(M>2m\)であるため、物体Mは鉛直下向きに加速し、物体mは鉛直上向きに加速します。このとき物体M、物体m、動滑車について、それぞれに働く力を以下のように図に記入しましょう。
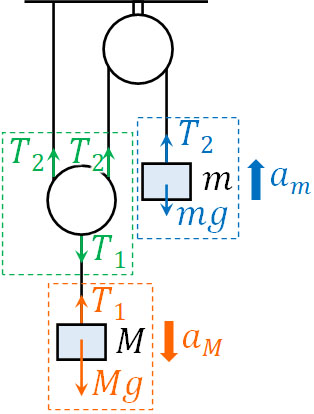
この場合、以下のように運動方程式を作ることができます。
- 物体M:\(Ma_M=Mg-T_1\)
- 物体m:\(ma_m=T_2-mg\)
- 動滑車:\(T_1=2T_2\)
なお、\(Ma_M=T_1-Mg\)としてはいけません。物体Mは下向きに加速しているからです。同様に、\(ma_M=mg-T_2\)としてはいけません。物体mは上向きに加速しているからです。
物理では、実際に物体が動いている場面を想像しなければ問題を解くことはできません。そこで、事前に物体がどちらに動くのか把握して運動方程式を作りましょう。
それでは、\(T_1=2T_2\)を\(Ma_M=Mg-T_1\)に代入しましょう。
\(Ma_M=Mg-T_1\)
\(Ma_M=Mg-2T_2\)
\(2T_2=Mg-Ma_M\)
次に\(ma_m=T_2-mg\)を2倍して、\(2T_2=Mg-Ma_M\)を代入しましょう。
\(ma_m=T_2-mg\)
\(2ma_m=2T_2-2mg\)
\(2ma_m=Mg-Ma_M-2mg\)
なお\(2a_M=a_m\)であるため、以下のように変換できます。
\(2ma_m=Mg-Ma_M-2mg\)
\(4ma_M=Mg-Ma_M-2mg\)
\(4ma_M+Ma_M=Mg-2mg\)
\(a_M(4m+M)=g(M-2m)\)
\(a_M=\displaystyle\frac{g(M-2m)}{4m+M}\)
こうして、\(a_M=\displaystyle\frac{g(M-2m)}{4m+M}\)とわかりました。また物体mの加速度は物体Mの加速度の2倍であるため、\(a_m=\displaystyle\frac{2g(M-2m)}{4m+M}\)です。
運動方程式(ニュートンの第二法則)の作り方を学ぶ
力学で最も重要な内容の一つが運動方程式(ニュートンの第二法則)です。物体が動いているとき、運動方程式を使うことで式を作りましょう。物体がつり合っているときとは異なり、加速度が加わっている状態であれば、運動方程式を作ることができます。
力を組み合わせることによって運動方程式を得られます。このとき、力の向きと加速度の向きが同じである必要があります。
なお運動方程式を作るとき、さまざまな種類の問題を解きましょう。2つの物体が糸でつながっていたり、滑車を利用していたりする問題を解くことによって運動方程式を作れるようにするのです。
物体が動いているときの性質を学び、それぞれの物体に着目して運動方程式を作りましょう。実際に問題をいくつも解くことにより、運動方程式を作れるようになります。






