電流と磁場は密接に関わっているため、電磁気学で磁場を学びます。特に重要な性質の一つとして、「磁場が存在するとき、電流が流れると電流は磁場から力を受ける」ことがあります。
電流が磁場から力を受けるとき、どの方向で力を受けるのか判断できるようになりましょう。フレミングの左手の法則を利用することにより、力の向きを判断できます。実際にあなたの左手を利用し、三次元での力の向きを把握しましょう。
また力の向きだけでなく、力の大きさを計算する必要があります。そこで、公式を利用して計算しましょう。また導線に電流を流すと磁場が発生するため、平行電流での磁場による影響を学びましょう。
それでは、どのようにフレミングの左手の法則を利用すればいいのでしょうか。また、どのように公式を活用して力の大きさを計算すればいいのでしょうか。電流が磁場から受ける力について解説していきます。
もくじ
電流が磁場を横切ると力を受ける:フレミングの左手の法則
電流が流れると磁場が発生します。そのため外部磁場が存在する場合、元々の磁場(外部磁場)と電流によって発生する磁場によって互いに影響し合い、力が加わります。
磁石では、N極とN極(またはS極とS極)は反発します。一方でN極とS極は引き合います。そのため電流が流れることにより、導線の周辺に磁場が発生して特定の方向に力が加わるのです。下図のように、磁場\(H\)に対して電流\(I\)が横切る場合、電流(導線)は磁場から力\(F\)を受けます。
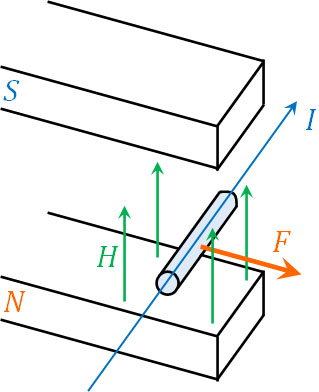
それでは、電流が流れることによってどの向きに力が加わるのでしょうか。磁場を学ぶとき、三次元で考える必要があるので複雑です。このとき役に立つのがフレミングの左手の法則です。フレミングの左手の法則では、中指・人差し指・親指を利用します。それぞれの指が電流、磁場、力を表します。
- 中指:電流
- 人差し指:磁場
- 親指:力

磁場によって電流が受ける力の方向を確認したい場合、必ずあなたの左手を利用しましょう。なおフレミングの左手の法則では、以下のようにすべて90°で交わることになります。
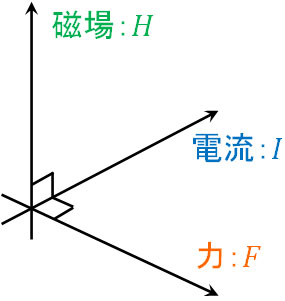
この関係を利用して電流(中指)と磁場(人差し指)の向きを合わせれば、力の向きがわかります。
電流が受ける力を計算する公式
それでは、電流が受ける力はいくらになるのでしょうか。磁場の大きさが\(H\)[A/m]であり、磁場を垂直に横切る導線の距離が\(l\)[m]、電流が\(I\)[A]のとき、力の大きさ\(F\)は比例定数\(μ\)を用いて以下のように表すことができます。
- \(F=μHIl\)
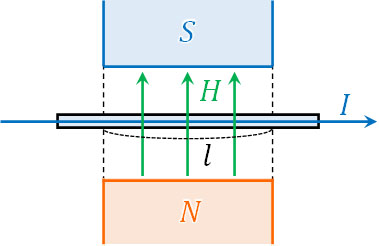
この公式の意味は容易に理解できます。磁場\(H\)が大きいほど、影響を受ける導線\(l\)が長いほど、電流\(I\)が大きいほど、それに比例して力\(F\)が大きくなるのは当然です。そこで磁場\(H\)、導線の長さ\(l\)、電流\(I\)の3つをかけましょう。
なお環境によって電流が受ける力の大きさは異なります。そこで、公式では比例定数\(μ\)を利用するのです。そうすれば、なぜ先ほどの公式を利用するのかわかります。なお、比例定数\(μ\)を透磁率といいます。
電流の向きが斜めのときの計算方法
それでは、電流の向きが斜めのときはどのように計算すればいいのでしょうか。力学を学んでいる場合、計算方法は簡単です。角度を利用して、磁場に対して垂直方向の電流の大きさを出しましょう。
なお、角度の場所によってsinθを利用するのか、それともcosθを利用するのかが異なります。いずれにしても以下のように角度を利用して、磁場に対して垂直となる電流の向きを計算しなければいけません。

左図の場合、電流と磁場の向きが垂直となるためには、\(Isinθ\)を利用すればいいとわかります。そのため、先ほどの公式を以下のように変形しましょう。
- \(F=μHIlsinθ\)
また右図の場合、電流と磁場の向きが垂直になるためには、\(Icosθ\)を利用すればいいとわかります。そのため、式は以下のようになります。
- \(F=μHIlcosθ\)
磁場と電流の向きが平行だと、磁場による力の影響はありません。そのため、磁場と電流の向きは必ず垂直でなければいけないことを理解しましょう。
平行電流が受ける力の大きさ
電流が流れている場合、磁場が発生しています。それでは、2つの電流が平行に存在する場合について、力の大きさはどのようになるのでしょうか。
例として、同じ向きに電流が流れている2つの導線があるとします。このうち、片方の電流に着目しましょう。そうすると「右ねじの法則により、もう一方の電流に対して垂直に磁場が発生する」とわかります。
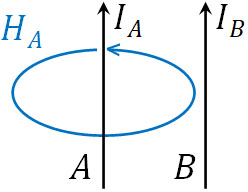
例えば上図の場合、電流\(I_A\)によって、電流Bに対して垂直に磁場が発生します。その結果、磁場\(H_A\)によって電流\(I_B\)に対して力が加わります。なおフレミングの左手の法則より、電流\(I_B\)に加わる力の向きは以下になります。
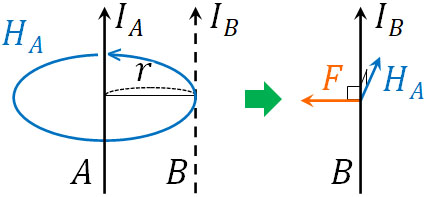
それでは、力\(F\)の大きさはどのように計算すればいいのでしょうか。公式より、電流が直線で進む場合、磁場の大きさは\(H=\displaystyle\frac{I}{2πr}\)によって計算できます。そのため、電流\(I_A\)による磁場の大きさは\(H_A=\displaystyle\frac{I_A}{2πr}\)です。
また、導線Bが\(l\)[m]あたりに受ける力の大きさ\(F\)は透過率\(μ\)を利用して\(F=μH_AI_Bl\)と表すことができます。そのため、以下のように計算できます。
\(F=μH_AI_Bl\)
\(F=μI_Bl×\displaystyle\frac{I_A}{2πr}\)
\(F=\displaystyle\frac{μI_AI_Bl}{2πr}\)
こうして、電流Bが受ける力は\(F=\displaystyle\frac{μI_AI_Bl}{2πr}\)[N]と計算できました。
なお、電流Aの影響によって電流Bに力が加わるというのは、電流Bによって電流Aに力が加わることも意味しています。つまり、電流Aと電流Bは互いに力を与えています。そこで、先ほどと同様にフレミングの左手の法則を利用すると、電流Bの影響によって電流Aは以下のように力を受けているとわかります。
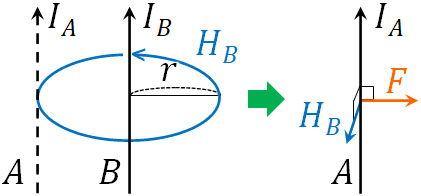
つまり、電流Aと電流Bには互いに引き合う力が働いています。また先ほどと同じように力の大きさを計算すると、電流Aに働く力は\(F=\displaystyle\frac{μI_AI_Bl}{2πr}\)[N]となります。当然ながら、電流Aと電流Bに働く力の大きさは同じです。
なお電流の向きが異なる場合、引き合う力ではなく、反発する力が働きます。磁場や電流の向きによって、力の方向が変化するのです。
磁場と電流によって発生する力に関する練習問題
それでは、電流が磁場によって受ける力について練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 下図のように直線の導線があり、電流\(I\)が矢印の向きに流れています。また、導線Aから\(x\)離れた場所にたての長さが\(a\)、横の長さが\(b\)である長方形のコイルがあり、\(\displaystyle\frac{I}{2}\)の電流が矢印の向きに流れています。透磁率が\(μ\)、円周率が\(π\)のとき、導線Aの電流からコイルが受ける力の大きさと向きを求めましょう。
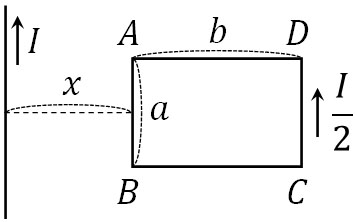
直線の導線では、電流が流れることによって磁場が発生しています。磁場とコイルを流れる電流が垂直であるため、それぞれの方向で力が働きます。フレミングの左手の法則を利用すると、力の向きはそれぞれ以下のようになります。
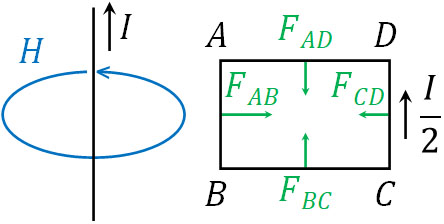
直線の導線から距離が離れるほど、コイルに加わる力が弱まります。このとき\(F_{BC}\)と\(F_{AD}\)は力の向きが反対であり、さらにはどの場所であっても導線からの距離が同じです。そのため力は打ち消し合い、力の向きに関与することはありません。
そこで、\(F_{AB}\)と\(F_{CD}\)を計算しましょう。
・\(F_{AB}\)の計算
まっすぐの導線によって発生する電場は\(H_{AB}=\displaystyle\frac{I}{2πx}\)です。またコイルについて、距離は\(a\)であり、電流は\(\displaystyle\frac{I}{2}\)なので、以下のように計算しましょう。
\(F_{AB}=μH_{AB}·\displaystyle\frac{I}{2}·a\)
\(F_{AB}=μ·\displaystyle\frac{I}{2πx}·\displaystyle\frac{I}{2}·a\)
\(F_{AB}=\displaystyle\frac{μI^2a}{4πx}\)
・\(F_{CD}\)の計算
まっすぐの導線によって発生する電場は\(H_{CD}=\displaystyle\frac{I}{2π(x+b)}\)です。またコイルについて、距離は\(a\)であり、電流は\(\displaystyle\frac{I}{2}\)なので、以下のように計算しましょう。
\(F_{CD}=μH_{CD}·\displaystyle\frac{I}{2}·a\)
\(F_{CD}=μ·\displaystyle\frac{I}{2π(x+b)}·\displaystyle\frac{I}{2}·a\)
\(F_{CD}=\displaystyle\frac{μI^2a}{4π(x+b)}\)
こうして、\(F_{AB}\)と\(F_{CD}\)がわかりました。なお、磁場から距離が離れていると力が弱まるため、\(F_{AB}>F_{CD}\)であるとわかります。そこで、以下のように計算しましょう。
\(F_{AB}-F_{CD}\)
\(=\displaystyle\frac{μI^2a}{4πx}-\displaystyle\frac{μI^2a}{4π(x+b)}\)
\(=\displaystyle\frac{μI^2a}{4π}\left(\displaystyle\frac{1}{x}-\displaystyle\frac{1}{x+b}\right)\)
\(=\displaystyle\frac{μI^2a}{4π}×\displaystyle\frac{b}{x(x+b)}\)
\(=\displaystyle\frac{μI^2ab}{4πx(x+b)}\)
こうして、コイルに加わる力は\(\displaystyle\frac{μI^2ab}{4πx(x+b)}\)と計算できました。また\(F_{AB}>F_{CD}\)であるため、コイルが受ける力の向きは図の右向きです。
磁場を利用し、電流が受ける力の向きと大きさを把握する
電流と磁場には密接な関係があります。磁場が存在する場合、電流が流れていると力を受けます。磁場と電流の向きが平行だと力は発生しないものの、磁場と電流の向きが垂直の関係にある場合、電流は磁場から力を受けます。
力の方向を確かめたい場合、フレミングの左手の法則を利用しましょう。あなたの左手を利用することにより、力の向きがわかります。
また公式を利用することにより、力の大きさを計算できるようになりましょう。公式として\(F=μHIl\)を利用することにより、電流が磁場から受ける力の大きさがわかります。
力の向きや大きさを計算するとき、三次元で考える必要があるため、磁場に関する問題は複雑です。そこでフレミングの左手の法則と公式の両方を利用できるようになりましょう。






