コンデンサーの極板間に物体を挿入することによって、電気容量を変化させることができます。このとき導体(金属)を入れることがあれば、不導体(絶縁体)を入れることもあります。
コンデンサー内に絶縁体を入れる場合、電気容量が大きくなります。コンデンサーに入れる絶縁体を誘電体といいます。
それでは、誘電体(絶縁体)をコンデンサー内に入れることにより、なぜ電気容量が大きくなるのでしょうか。また、誘電体をコンデンサー内に挿入後、電気容量をどのように計算すればいいのでしょうか。
公式を覚えるのではなく、電気容量を得る計算方法を理解しましょう。そこで、誘電体を利用することによる誘電率の変化を解説していきます。
もくじ
絶縁体を挿入するとコンデンサーの電気容量が大きくなる
コンデンサーの極板間に物体が存在する場合、コンデンサーの電気容量が変化します。特に誘電体を極板間に挿入する場合、コンデンサーの電気容量が大きくなります。
誘電体とは、不導体(絶縁体)と意味が同じと考えましょう。電気を通さない物体をコンデンサーの極板間に入れると、電気容量が増えるのです。
電気容量を計算するとき、比例定数として誘電率を利用します。真空中の誘電率を\(ε_0\)、誘電体の誘電率を\(ε\)とすると、電気容量\(C\)は以下のように変化します。
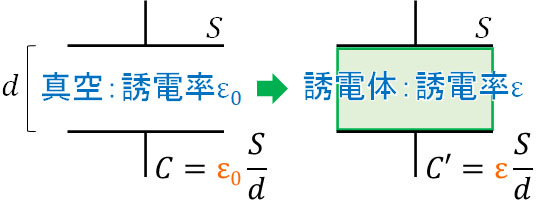
このように、真空での誘電率\(ε_0\)を誘電体の誘電率\(ε\)に変えることによって、コンデンサーの電気容量\(C\)を計算できます。
誘電率と比誘電率の関係と公式
それでは、真空中の誘電率と誘電体の誘電率を公式として表しましょう。操作前の電気容量を\(C\)、誘電体を挿入後の電気容量を\(C’\)とすると、前述の通り以下のように表すことができます。
- \(C=ε_0\displaystyle\frac{S}{d}\)
- \(C’=ε\displaystyle\frac{S}{d}\)
そこで真空中の誘電率\(ε_0\)と誘電体の誘電率\(ε\)を利用して、以下のように公式を作りましょう。
- \(ε=ε_r·ε_0\)
\(ε_r\)を比誘電率といいます。比誘電率\(ε_r\)とは、真空中の誘電率\(ε_0\)を何倍すると、誘電体の誘電率\(ε\)になるのかを表す値です。当然、誘電体によって誘電率\(ε\)は異なるため、比誘電率\(ε_r\)も変化します。
絶縁体の中でも、高い比誘電率を持つ物体が誘電体です。高い比誘電率\(ε_r\)をもつ物体では、コンデンサーの電気容量を効率的に大きくできます。
比誘電率を利用してコンデンサーの電気容量を計算する
元々の誘電率(真空中の誘電率)\(ε_0\)に対して、比誘電率\(ε_r\)をかけることにより、誘電体の誘電率\(ε\)を得ることができます。つまり、元々の電気容量に対して、比誘電率\(ε_r\)をかけることにより、誘電体を極板間に挿入した後の電気容量の計算が可能です。
前述の通り、\(C’=ε\displaystyle\frac{S}{d}\)です。そこで\(ε=ε_r·ε_0\)を利用して、以下のように公式を変形しましょう。
\(C’=ε\displaystyle\frac{S}{d}\)
\(C’=ε_r×ε_0\displaystyle\frac{S}{d}\)
\(C’=ε_rC\)
こうして、「絶縁体が存在しない場合の電気容量\(C\)に対して比誘電率\(ε_r\)をかけることで、誘電体の電気容量\(C’\)を得られる」とわかりました。
真空中の誘電率や誘電体の誘電率、比誘電率の関係を理解していれば、ここまで解説した公式を覚える必要はありません。公式を覚えなくても、比誘電率を利用することによって公式を作ることができます。
誘電体を入れると電気容量が増える理由
それでは、電荷を有するコンデンサーに対して誘電体(絶縁体)を極板間に入れると、なぜ電気容量が増えるのでしょうか。この理由を理解しましょう。
充電されているコンデンサーには電荷があります。正の電荷と負の電荷があるため、極板間には電場が発生しています。
そこで極板間(電場が発生している場所)に不導体を入れると、どのような現象が起こるでしょうか。導体とは異なり、不導体では電子は自由に動くことができません。ただ電場の影響は受けます。そのため以下のように、同じ原子内で電子の偏りを生じます。電子は正の電荷へ引き寄せられるのです。
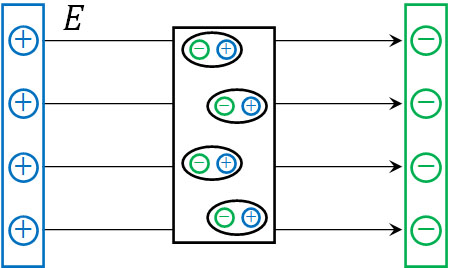
つまり、電場が発生している場所に不導体(誘電体:絶縁体)を入れると誘電分極が起こります。また誘電分極により、不導体の内部で新たな電場が発生します。元々の電場とは逆向きに不導体内部で電場が発生するため、電場の打ち消し合いにより、不導体内では外部の電場\(E\)が弱まります。
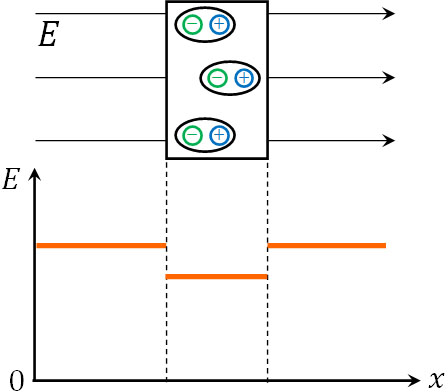
この現象は既に学んでいるはずなので、問題なく理解できると思います。
電場が弱くなり、電位差が小さくなった結果、電気容量が増加する
電位差は\(V=Ed\)によって計算できます。導体を極板間に入れ、誘導体内部の電場が\(E’\)になると、電位差は\(V=E’d\)となります。誘導体内部の電場\(E’\)は真空中の電場\(E\)よりも値が小さいため、電位差\(V\)の値も小さくなります。
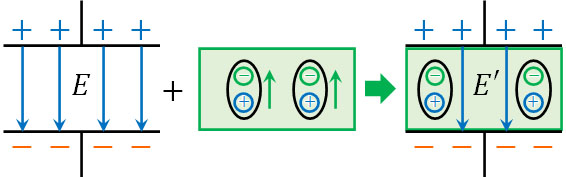
一方、コンデンサーでは極板が独立しているため、電荷の移動はなく、電気量\(Q\)は一定です。電気量\(Q\)を得る公式は以下になります。
- \(Q=CV\)
前述の通り、誘電体を極板間に入れることで電位差\(V\)が小さくなります。ただ電気量\(Q\)は一定であるため、電気容量\(C\)の値は大きくなるのです。
誘電体を利用して合成容量を計算する練習問題
それでは、誘電体を利用することで電気容量がどのように変化するのか計算しましょう。以下の問題の答えは何でしょうか。
- 真空のとき、電気容量が\(C\)のコンデンサーがあります。
- コンデンサーの右半分に比誘電率が3の誘導体を挿入する場合、電気容量はいくらですか。
- コンデンサーの下半分に比誘電率が3の誘導体を挿入する場合、電気容量はいくらですか。
1) コンデンサーの右半分に比誘電率が3の誘導体を挿入する場合、電気容量はいくらですか
コンデンサーの右半分に誘電体を挿入する場合、以下のように2つのコンデンサーが並列接続されているとみなすことができます。

また極板の面積を\(S\)、極板間の距離を\(d\)、真空中の誘電率を\(ε_0\)とすると、左半分の電気容量\(C_1\)と右半分の電気容量\(C_2\)は以下のようになります。
\(C_1=ε_0\displaystyle\frac{\displaystyle\frac{S}{2}}{d}=ε_0\displaystyle\frac{S}{2d}\)\(=\displaystyle\frac{C}{2}\)
\(C_2=3ε_0\displaystyle\frac{\displaystyle\frac{S}{2}}{d}=3ε_0\displaystyle\frac{S}{2d}\)\(=\displaystyle\frac{3C}{2}\)
\(C=ε_0\displaystyle\frac{S}{d}\)であるため、このような答えになります。またコンデンサーは並列接続であるため、足し算によって合成容量\(C’\)を計算しましょう。
\(C’=\displaystyle\frac{C}{2}+\displaystyle\frac{3C}{2}=2C\)
こうして、電気容量は\(2C\)になるとわかります。
2) コンデンサーの下半分に比誘電率が3の誘導体を挿入する場合、電気容量はいくらですか
コンデンサーの下半分に誘電体を入れる場合、直列接続によって2つのコンデンサーが存在すると考えることができます。そのため、以下の図を作りましょう。
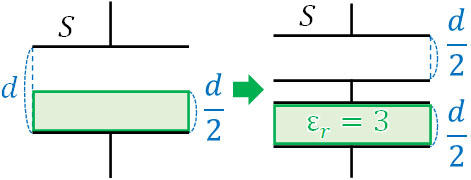
上半分の電気容量\(C_1\)と下半分の電気容量\(C_2\)は以下のようになります。
\(C_1=ε_0\displaystyle\frac{S}{\displaystyle\frac{d}{2}}=ε_0\displaystyle\frac{2S}{d}\)\(=2C\)
\(C_2=3ε_0\displaystyle\frac{S}{\displaystyle\frac{d}{2}}=ε_0\displaystyle\frac{6S}{d}\)\(=6C\)
そこで合成容量\(C’\)を計算しましょう。
\(\displaystyle\frac{1}{C’}=\displaystyle\frac{1}{2C}+\displaystyle\frac{1}{6C}\)
\(\displaystyle\frac{1}{C’}=\displaystyle\frac{4}{6C}\)
\(C’=\displaystyle\frac{3C}{2}\)
こうして、コンデンサーの電気容量(合成容量)は\(\displaystyle\frac{3C}{2}\)になるとわかります。
誘電体の誘電率を利用して電気容量を得る
コンデンサーの極板間に物体を挿入することにより、電気容量が変わります。誘電体(絶縁体)を入れる場合、電気容量が大きくなります。不導体は電気を通さないため、誘電分極によって電場を弱めます。この働きによって電場が弱まり、電位差が小さくなり、結果として電気容量が大きくなるのです。
真空中の誘電率\(ε_0\)ではなく、誘電体の誘電率\(ε\)を利用すれば、誘電体を極板間に入れた後の電気容量を計算できます。
また、「真空中の誘電率\(ε_0\)を何倍すれば誘電体の誘電率\(ε\)になるのか」を表す指標に比誘電率\(ε_r\)があります。比誘電率\(ε_r\)を利用すれば、絶縁体をコンデンサー内に挿入した後の電気容量の計算が容易です。
コンデンサーの極板間に物体があると、電気容量が変化します。そこで誘電体をコンデンサー内に入れるとき、どのような現象が起こるのか理解しましょう。






