物理で電磁気を学ぶとき、最初に理解しなければいけない内容が静電気です。静電気を学ぶことにより、電気が発生する仕組みがわかります。原子の構造や帯電が起こる仕組みを学ぶことを通して、電気の基礎知識を身に付けるのです。
なお、すべての物質が電気を通すわけではありません。物質には、電気を通しやすい導体と、電気を通しにくい不導体(絶縁体)があります。導体では静電誘導という現象が起こり、不導体では誘電分極という現象が起こります。
また静電気で必ず覚えなければいけない公式にクーロンの法則があります。静電気力(クーロン力)の大きさを計算するとき、クーロンの法則を利用します。
それでは、静電気はなぜ発生するのでしょうか。また、どのように電気量の計算をすればいいのでしょうか。電磁気の初歩である静電気について解説していきます。
もくじ
電気の基本知識と用語の解説
電磁気を理解するためには、電気に関する基本的な知識と用語を学ばなければいけません。物体がもつ電気を電荷といいます。またどれだけの電荷が存在するのか表す量を電気量と呼び、電気量の単位はC(クーロン)です。多くの場合、電気量は記号\(Q\)を利用します。
知っている通り、電荷には正電荷と負電荷があります。
- 正電荷:\(Q>0\)
- 負電荷:\(Q<0\)
正電荷同士は反発します。この力を斥力(せきりょく)といいます。一方で正電荷と負電荷では、互いに引き合います。この力を引力といいます。また、こうした電荷の間に働く力を静電気力(クーロン力)といいます。
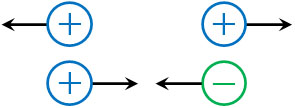
当然、電気量が大きくなると、その分だけ静電気力も大きくなります。また距離が近くなると、静電気力は大きくなります。
原子の構造と電気素量
それでは、なぜ静電気が発生するのでしょうか。原子の構造を確認することによって、電気が帯電する理由を理解しましょう。
すべての原子には陽子と電子があります。化学を学んでいる場合、原子に陽子や中性子、電子が存在することは既に知っていると思います。また、陽子と電子の数が必ず同じになることも理解していると思います。
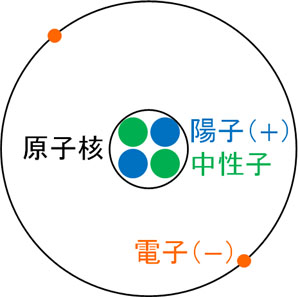
このとき、一つの陽子がもつ電気量と一つの電子がもつ電気量は以下のようになります。
- 陽子:\(1.6×10^{-19}\) C
- 電子:\(-1.6×10^{-19}\) C
\(1.6×10^{-19}\)Cは電気量の最小単位であり、これを電気素量といいます。電気素量は記号\(e\)で表すことが多いです。つまり陽子一つの電気量は\(e\)であり、電子一つの電気量は\(-e\)です。
帯電が起こる仕組み:電気量保存の法則
原子は陽子(正電荷)と電子(負電荷)の数が同じです。また、陽子と電子を比較すると電気量の絶対値は同じです。そのため、通常だと原子は帯電していません。
ただ場合によっては、原子は電子を放出することがあります。陽子や中性子に比べて、電子の質量は非常に小さいです。そのため陽子(正電荷)は動かないものの、電子(負電荷)は動くケースがあるのです。
原子から電子が放出されると、負電荷がなくなるので原子はプラスに帯電します。一方で物体が電子を受け取ると、負電荷の数が多くなるのでマイナスに帯電します。電子が移動することによって電気を帯びるのです。
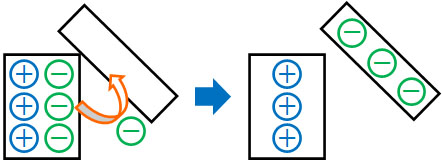
なお、電子がどちらの物体に移動するのかについては、物体の種類によって異なります。
導体と不導体(絶縁体):金属は電気を通しやすい
ただ知っている通り、多くの物体は電気を通しません。電気を通すのは多くの場合、金属です。金属で静電気が発生しやすいのは、金属が電気を通しやすいからなのです。
電気を通しやすい物体を導体、電気を通しにくい物体を不導体(絶縁体)といいます。金属は導体であり、ゴムやガラス、紙などは不導体です。
金属が電気を通す理由は化学で学びます。金属は金属結合によって原子が結合しています。金属結合には、金属元素全体で電子を共有する性質があります。つまり金属結合では電子が自由に動き回ることができ、電子(自由電子)が移動することによって帯電するのです。
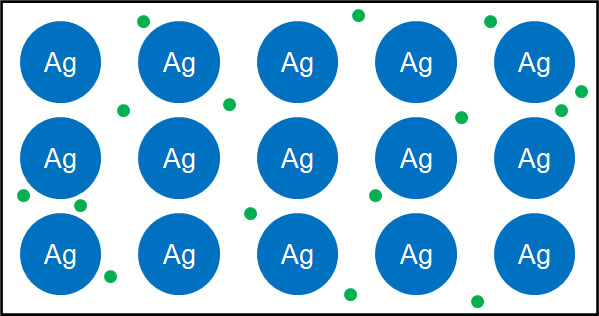
一方で金属結合していない物体では、電子は自由に動き回ることができません。金属に自由電子があるからこそ、金属は電気を通すのです。
導体による静電誘導と不導体による誘電分極
それでは帯電している物体(帯電体)を近づける場合、どのような現象が起こるのでしょうか。結論を述べると、以下のようになります。
- 導体:電子が移動し、電荷が表れる(静電誘導)
- 不導体:電子がわずかに移動し、不導体が少し帯電する(誘電分極)
金属などの導体では、自由電子は自由に動くことができます。例えば正に帯電している物体を導体に近づけると、自由電子は正の帯電体に近づきます。
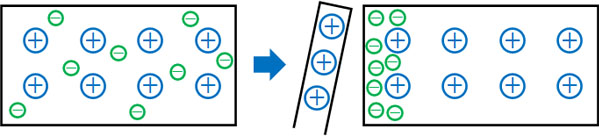
帯電体がない場合、自由電子は物体全体に散らばって存在しています。しかし帯電体が近くにあると、電子は正の帯電体へ引き寄せられた結果、正の帯電体に近い部分がマイナスとなり、その反対側がプラスになるのです。
一方で負の帯電体を導体に近づける場合、負の帯電体に近い部分がプラスとなり、その反対側がマイナスになります。
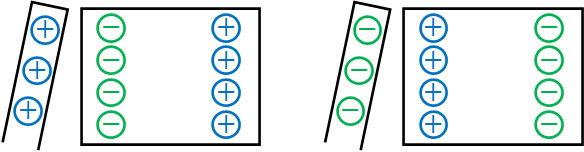
この現象を静電誘導といいます。導体では、電荷を帯びている物体を近づけることによって静電誘導が起こるのです。
・不導体での誘電分極
一方で不導体では、静電誘導ではなく誘電分極が起こります。電荷を帯びている物体(帯電体)を近づけることにより、不導体が少し電荷を帯びる現象が誘電分極です。
不導体(絶縁体)にも関わらず、帯電体を近づけることによって不導体はなぜ電荷を帯びるのでしょうか。不導体は金属とは異なり、自由電子がありません。そのため、電子が自由に動くことはできません。
電子は原子の周囲に留まるものの、帯電体が近づくことによって、原子内で電子の偏りが発生します。例えば正の帯電体を近づける場合、電子が原子核から離れることはないものの、電子は正の帯電体に引っ張られるのです。
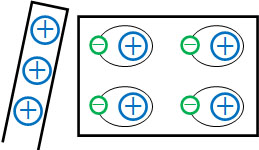
こうして、原子に着目するとわずかにプラスに荷電した部分とマイナスに荷電した部分が表れます。この現象が誘電分極です。
クーロンの法則と公式:静電気力(クーロン力)の大きさ
それでは、静電気力(クーロン力)の大きさはどのように計算すればいいのでしょうか。静電気力を計算するとき、クーロンの法則が利用されます。
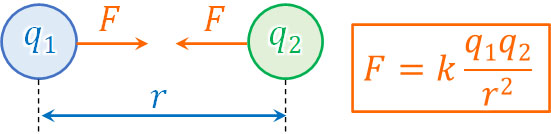
クーロンの法則では、2つの電荷の電気力が\(q_1\)[C]と\(q_2\)[C]であり、距離が\(r\)[m]離れているとき、以下の2つが成り立ちます。
- クーロン力は\(q_1\)と\(q_2\)の積に比例する
- クーロン力は距離\(r\)の2乗に反比例する
これがクーロンの法則であり、静電気力の大きさ\(F\)[N]は以下の公式で表すことができます。
- \(F=k\displaystyle\frac{q_1q_2}{r^2}\)
なお、\(k\)は比例定数(クーロン定数)であり値が決まっています。\(k\)の値は約9.0×109 [N·m2/C2]です。
参考までに、静電気力を得る公式は万有引力の公式とほぼ同じです。力学で学ぶ万有引力の公式は以下になります。
- \(F=G\displaystyle\frac{mM}{r^2}\)
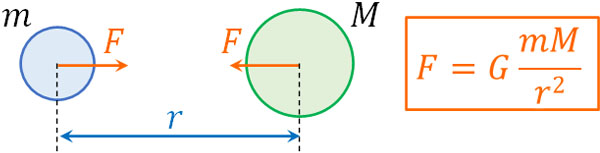
物理を学ぶとき、クーロンの法則も万有引力の公式も覚えなければいけません。そこで両者の公式がほぼ同じであることを理解すれば、あなたが覚えなければいけない公式が減ります。
静電気力を計算する練習問題
それでは、練習問題を解いてクーロン力の計算をしましょう。以下の問題の答えは何でしょうか。
- 天井の点Oから物体Aと物体Bをつるし、正に帯電させると図のように45°と30°で静止しました。物体Aと物体Bの高さは同じであり、2つの物体の水平方向と点Oの高さは\(h\)です。物体Aの電気量が\(q\)、物体Aの質量が\(m\)、クーロン定数が\(k\)、重力加速度が\(g\)のとき、物体Bの質量\(m_B\)と電気量\(q_B\)はいくらですか。
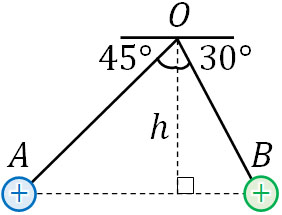
2つの物体は静止しているため、力のつり合いの式を作りましょう。なお力のつり合いの式を作るとき、クーロン力(今回のケースでは正と正の電荷による反発力)が加わっているため、これを加味する必要があります。
図を作ると以下のようになります。
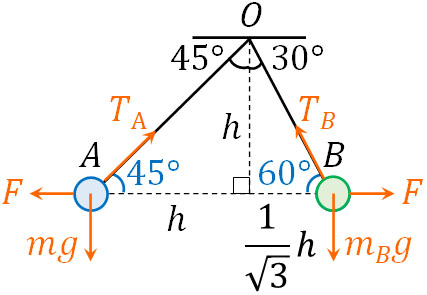
上図において水平方向に着目すると、以下の力のつり合いの式を作ることができます。
\(F=T_Acos45°=T_Bcos60°\)
\(F=\displaystyle\frac{1}{\sqrt{2}}T_A=\displaystyle\frac{1}{2}T_B\)
次に垂直方向に着目しましょう。つり合いの式は以下になります。
- \(mg=\displaystyle\frac{1}{\sqrt{2}}T_A\)
- \(m_Bg=\displaystyle\frac{\sqrt{3}}{2}T_B\)
\(F=\displaystyle\frac{1}{\sqrt{2}}T_A\)と\(mg=\displaystyle\frac{1}{\sqrt{2}}T_A\)より、\(F=mg\)です。また\(T_A=\sqrt{2}mg\)です。
なお\(\displaystyle\frac{1}{\sqrt{2}}T_A=\displaystyle\frac{1}{2}T_B\)より、以下のように計算できます。
\(T_B=\displaystyle\frac{2}{\sqrt{2}}T_A\)
\(T_B=\sqrt{2}T_A\)
\(T_B=2mg\)
そこで、\(T_B=2mg\)を\(m_Bg=\displaystyle\frac{\sqrt{3}}{2}T_B\)に代入しましょう。
\(m_Bg=\displaystyle\frac{\sqrt{3}}{2}×2mg\)
\(m_B=\sqrt{3}m\)
こうして、物体Bの質量は\(\sqrt{3}m\)とわかりました。
次に、物体Bの電気量\(q_B\)を計算しましょう。先ほどの計算より、静電気力\(F\)は\(mg\)と計算できています。そこで、クーロンの法則を用いて以下の式を作りましょう。
\(mg=k\displaystyle\frac{q·q_B}{\left(h+\displaystyle\frac{h}{\sqrt{3}}\right)^2}\)
\(mg=k\displaystyle\frac{q·q_B}{\left(\displaystyle\frac{\sqrt{3}h+h}{\sqrt{3}}\right)^2}\)
\(mg=3k\displaystyle\frac{q·q_B}{3h^2+2\sqrt{3}h^2+h^2}\)
\(mg=3k\displaystyle\frac{q·q_B}{2h^2(2+\sqrt{3})}\)
\(q_B=\displaystyle\frac{2mgh^2(2+\sqrt{3})}{3kq}\)
こうして、物体Bの電気量\(q_B\)は\(\displaystyle\frac{2mgh^2(2+\sqrt{3})}{3kq}\)とわかりました。
電気の基礎知識を学び、クーロン力の計算を行う
電磁気を学ぶとき、最も基本的な内容が静電気です。そこで電気の基礎知識や原子の構造、帯電の仕組みを理解しましょう。原子は陽子と電子をもっているため、電荷の偏りによって静電気が発生するのです。
なお物体によって電気の通しやすさが異なります。多くの物体は不導体(絶縁体)です。一方、金属は自由電子をもつ導体であり、電気を通します。帯電体を導体に近づけると静電誘導が起こり、帯電体を不導体に近づけると誘電分極が起こります。
また静電気で重要な法則がクーロンの法則です。クーロンの法則の公式を覚え、計算問題を解けるようにしましょう。
電気量や静電気力を計算するとき、力学の知識も必要になります。そこで物理で必要な知識を利用し、電気の基礎である静電気を学びましょう。






