質量が理由なく増えたり消えたりすることはありません。そのため、化学では質量保存の法則を学びます。
ただ物理では、質量保存の法則が成り立たないケースがあります。原子核の状態によって、質量が多くなったり、反対に質量が少なくなったりするのです。これには、結合エネルギーという概念が関わっています。
結合エネルギーを利用することにより、核反応(核分裂、核融合など)が起こる原理を学ぶことができます。核反応によって質量が変化し、これには結合エネルギーが関与しているのです。
それでは、結合エネルギーとは何でしょうか。また、なぜ質量保存の法則が成り立たないのでしょうか。核反応で起こる現象を解説していきます。
もくじ
特殊相対性理論による静止エネルギー
20世紀に活躍した偉大な物理学者にアインシュタインがいます。彼は特殊相対性理論を発表し、静止している物体についてもエネルギーをもつと考えました。
物理で学ぶエネルギーには力学的エネルギーや熱エネルギー、電気エネルギーなど、多くの種類のエネルギーがあります。これらのエネルギーに加えて、彼は「質量がエネルギーをもつ」と考えたのです。
詳しい説明を省きますが、質量\(m\)[kg]の物体がもつエネルギー\(E\)[K]は以下の式によって表すことができます。
- \(E=mc^2\)
※\(c\)[m/s]は真空中の光の速さ
動いている物体は運動エネルギーをもつものの、静止している物体はエネルギーをもたないと考えてしまいます。ただ、アインシュタインは静止している物体についても、存在するだけでエネルギーをもつと考えたのです。なお、先ほどの式で表されるエネルギーを静止エネルギーといいます。
つまり質量というのは、エネルギーと意味が同じです。質量はエネルギーの一種であり、質量が大きいほど、静止していたとしても大きなエネルギーを保有することになるのです。
質量欠損と原子核の重さ
それでは、なぜ静止エネルギーが重要なのでしょうか。私たちの日常生活では、質量保存の法則が成り立ちます。30kgの物体と50kgの物体を乗せると、必ず80kgになります。ただ原子核を調べていた研究者は「質量保存の法則が成り立たないケースがある」と報告しました。
陽子と中性子は質量がほぼ同じであるため、一つの陽子(または中性子)の質量を\(m\)としましょう。陽子の数が\(Z\)、中性子の数が\(N\)の場合、原子核の質量\(M\)は以下のように表すことができます。
- \(M=m(Z+N)\)
この式については、何も問題なく理解できると思います。ただ場合によっては、この式が成り立たないケースがあるのです。特定の条件では、以下のようになる場合があります。
- \(M<m(Z+N)\)
つまり、「原子核に陽子と中性子がまとまって存在している状態\(M\)」と「陽子と中性子がバラバラに存在している状態\(m(Z+N)\)」を比較すると、陽子と中性子が別々に存在しているほうが質量は大きくなります。
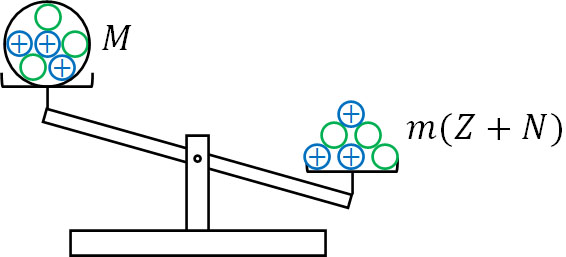
このとき、質量の差\(Δm\)は以下の式によって表すことができます。
- \(Δm=m(Z+N)-M\)
質量の差\(Δm\)を質量欠損といいます。また質量はエネルギーでもあるため、質量欠損が起こった分だけ、エネルギーが減少していることになります。そこで静止エネルギーの公式を利用すると、質量欠損に相当する静止エネルギーを以下のように表すことができます。
- \(ΔE=Δmc^2\)
つまり原子核の状態というのは、陽子と中性子がバラバラで存在している状態よりも、\(ΔE=Δmc^2\)の分だけエネルギーが低いのです。
静止エネルギーと結合エネルギーの関係
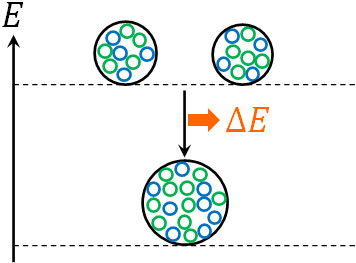
それでは、質量欠損での静止エネルギーは何を意味しているのでしょうか。先ほど、原子核の状態よりも、バラバラの状態のほうが重いと解説しました。そこで、保有するエネルギーを基準に図を作りましょう。
重い物体であるほど静止エネルギーをもつため、原子核の状態では、静止エネルギーが低くなります。ここに質量欠損に相当する静止エネルギーとして\(ΔE=Δmc^2\)を加えると、バラバラの状態のエネルギーになります。
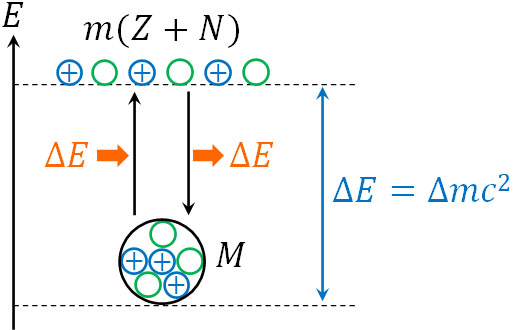
こうして、バラバラの状態では質量欠損\(Δm\)の分だけ質量が重くなります。
またバラバラの状態から質量欠損に相当する静止エネルギーが放出されると、原子核の状態になれます。なお静止エネルギーの放出により、質量欠損\(Δm\)の分だけ軽くなります。
このように原子核の状態からバラバラの状態にしたり、反対にバラバラの状態から原子核の状態に戻したりするとき、\(ΔE\)のエネルギーを与える(または放出する)ことになります。このエネルギー\(ΔE\)を結合エネルギーといいます。
原子核反応により、原子核が変化する
次に核反応(原子核反応)を解説します。原子核が粒子と衝突することにより、異なる原子核に変わる現象を核反応といいます。
人工的に核反応を成功させた人にラザフォードがいます。1919年、彼は窒素の原子核(\(_7^{14}N\))に対してα線(\(_2^4He\))を照射しました。そうすると、窒素が酸素(\(_8^{17}O\))へ変わることを彼は発見しました。このとき、酸素のほかに陽子(\(_1^1H\))も検出されました。
つまり、以下の核反応が観察されました。
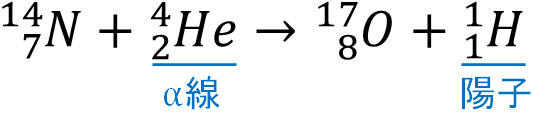
通常の化学反応では、元素が変化することはありません。一方で核反応では、原子核の種類が変化してしまうのです。なお核反応では、質量数の合計と陽子数の合計は同じです。先ほどの反応では、以下のようになっています。
- 質量数:\(14+4=17+1\)
- 陽子数(原子番号):\(7+2=8+1\)
核反応ではα線ではなく、陽子(\(_1^1H\))やβ線(\(_{-1}^0e\))、中性子線(\(_0^1n\))を利用して核反応させることも多いです。この場合であっても、質量数と陽子数の合計は常に同じです。
核分裂による結合エネルギーと質量の変化
なお質量数(陽子と中性子の数)は必ず一致するものの、全体の質量は変化します。静止エネルギーの吸収または放出により、原子核の重さが変わるのです。静止エネルギーが変化するというのは、質量が変化することを意味します。
核反応の一つに核分裂があります。一つの原子核が複数の原子核に分裂する現象を核分裂といいます。質量数の大きい原子核では、質量数の小さい原子核に分裂するほうが低いエネルギーとなるのです。
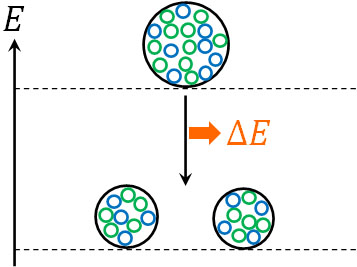
結合エネルギー\(ΔE\)を放出し、エネルギーが低くなるというのは、その分だけ質量の合計が少なくなることを意味しています。
例えばウランUの原子核に対して中性子線\(_0^1n\)を当てると、クリプトンKとバリウムBaが発生します。同時に3つの中性子線が放出されるため、以下の核分裂が起こります。
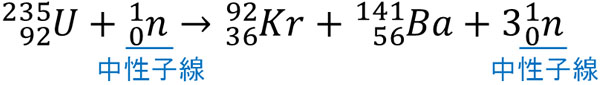
反応式を見てわかる通り、新たに中性子線が3つ放出されるため、中性子線が他のウランに当たることによって連続的に核分裂が起こります。これを連鎖反応といいます。原子力発電所では、連鎖反応を利用することによって大きなエネルギーを得て発電をしています。
核融合によってエネルギーが放出され、質量が軽くなる
ここまで、原子核が分裂することによって結合エネルギーが放出され、質量が軽くなると解説しました。ただ正確には、この説明は間違っています。
結合エネルギーを基準にすると、鉄(\(^{56}Fe\))が最も安定した原子核となります。つまり、ウランのように質量数が56よりも大きい場合、核分裂によって複数の原子核に分かれ、結合エネルギーを放出して質量を軽くします。
一方、質量数が56よりも小さい原子核の場合、質量数を多くするほうが安定します。そのため軽い原子核は複数の原子核と合体することにより、質量数を増やすことによって安定化しようとします。この反応を核融合といいます。
2つの軽い原子核が核融合によって合体し、異なる原子核になる場合、質量数は56に近づくので結合エネルギーを放出します。結合エネルギーを放出するというのは、その分だけ質量が少なくなることを意味しています。
核融合を利用する場合、水素を反応させることによってヘリウムを得ることができます。以下の反応が核融合です。
- \(4_1^1H+2e^-→_2^4He\)
水素を利用し、得られる物質はヘリウムであるため、クリーンエネルギーの一つが核融合です。太陽など、恒星は核融合によって莫大なエネルギーを生み出しています。なおエネルギーを放出しているため、太陽の質量は常に減少しています。
核反応によって発生するエネルギーを計算する
それでは、核分裂や核融合などの反応によって発生するエネルギーを計算してみましょう。以下の問題の答えは何でしょうか。
- 静止している物体が質量\(m\)と質量\(M\)の物体に分裂し、反対方向に\(v\)と\(V\)の速さで動きます。なお質量\(m\)の物体がもつ運動エネルギーを\(E_m\)、質量\(M\)の物体がもつ運動エネルギーを\(E_M\)、光の速さを\(c\)とします。
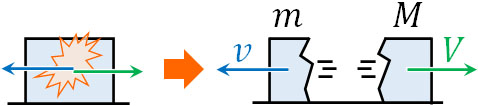
- 運動エネルギー\(E_m\)と\(E_M\)の比はいくらですか。なお、\(m\)と\(M\)を用いて表しましょう。
- 静止しているウランU原子核がα崩壊し、トリウムTh原子核へ変化しました。発生するエネルギー\(E\)はいくらですか。なお、ウラン原子核の質量を\(M_U\)、トリウム原子核の質量を\(M_{Th}\)、α粒子の質量を\(m_α\)とします。
- \(E\)を利用して、α粒子の運動エネルギー\(E_α\)を求めましょう。なお、発生したエネルギー\(E\)はすべてトリウムTh原子核とα粒子の運動エネルギーに利用されるとします。
1) 運動エネルギー\(E_m\)と\(E_M\)の比はいくらですか。なお、\(m\)と\(M\)を用いて表しましょう
運動量保存則より、以下の計算をすることができます。
\(mv=MV\)
\(\displaystyle\frac{v}{V}=\displaystyle\frac{M}{m}\)
また\(E_m=\displaystyle\frac{1}{2}mv^2\)であり、\(E_M=\displaystyle\frac{1}{2}MV^2\)です。そのため、以下のように計算しましょう。
\(\displaystyle\frac{E_m}{E_M}=\displaystyle\frac{\displaystyle\frac{1}{2}mv^2}{\displaystyle\frac{1}{2}MV^2}\)
\(\displaystyle\frac{E_m}{E_M}=\displaystyle\frac{m}{M}·\displaystyle\frac{v^2}{V^2}\)
\(\displaystyle\frac{E_m}{E_M}=\displaystyle\frac{m}{M}·\displaystyle\frac{M^2}{m^2}\)
\(\displaystyle\frac{E_m}{E_M}=\displaystyle\frac{M}{m}\)
こうして、\(E_m\)と\(E_M\)の運動エネルギーの比は\(E_m:E_M=M:m\)とわかりました。
2) 静止しているウランU原子核がα崩壊し、トリウムTh原子核へ変化しました。発生するエネルギー\(E\)はいくらですか。なお、ウラン原子核の質量を\(M_U\)、トリウム原子核の質量を\(M_{Th}\)、α粒子の質量を\(m_α\)とします
ウランは質量数が大きいため、質量数を減らすことによって安定になろうとします。言い換えると、ウランはエネルギーを放出するのです。そこで、ウランがα崩壊するときに放出する結合エネルギー(発生するエネルギー)を計算しましょう。
エネルギーを放出することにより、その分だけウランの原子核は軽くなります。このとき、質量の変化量\(Δm\)は以下のようになります。
- \(Δm=M_U-(M_{Th}+m_α)\)
そこで、静止エネルギーを得る公式に代入しましょう。
\(E=Δmc^2\)
\(E=(M_U-M_{Th}-m_α)c^2\)
こうして、発生するエネルギーは\(E=(M_U-M_{Th}-m_α)c^2\)とわかりました。
3) \(E\)を利用して、α粒子の運動エネルギー\(E_α\)を求めましょう。なお、発生したエネルギー\(E\)はすべてトリウムTh原子核とα粒子の運動エネルギーに利用されるとします
発生したエネルギー\(E\)はすべてトリウムTh原子核とα粒子の運動エネルギーに利用されるため、トリウムの運動エネルギーを\(E_{Th}\)とすると、以下の式を作れます。
- \(E=E_{Th}+E_α\)
また(1)の結果より、\(\displaystyle\frac{E_m}{E_M}=\displaystyle\frac{M}{m}\)です。つまり、以下のようになります。
\(\displaystyle\frac{E_{Th}}{E_α}=\displaystyle\frac{m_α}{M_{Th}}\)
\(E_{Th}=\displaystyle\frac{m_αE_α}{M_{Th}}\)
そこで、\(E_{Th}=\displaystyle\frac{m_αE_α}{M_{Th}}\)を\(E=E_{Th}+E_α\)に代入しましょう。
\(E=E_{Th}+E_α\)
\(E=\displaystyle\frac{m_αE_α}{M_{Th}}+E_α\)
\(E=E_α·\displaystyle\frac{m_α+M_{Th}}{M_{Th}}\)
\(E_α=E\displaystyle\frac{M_{Th}}{m_α+M_{Th}}\)
こうして、α粒子の運動エネルギーは\(E_α=E\displaystyle\frac{M_{Th}}{m_α+M_{Th}}\)とわかりました。
質量欠損と結合エネルギーの概念を学び、核反応を理解する
原子のようなミクロの世界では、通常では考えられない現象が起こります。その一つが質量欠損であり、質量保存の法則が成り立ちません。
この問題を解決したのがアインシュタインであり、彼は静止している物質であってもエネルギーをもつと考えました。特殊相対性理論の詳細を省くと、\(E=mc^2\)によって静止エネルギーを計算できます。
質量欠損と結合エネルギーの概念を知れば、核反応が起こるときに発生するエネルギーや物体の運動エネルギー、失われる物体の質量などを計算できます。そこで結合エネルギーを利用して、核分裂や核融合が起こるときの計算を行えるようにしましょう。
「質量がエネルギーをもつ」と学ぶと、核分裂や核融合によってなぜ質量が変化するのか理解できます。原子核でどのような現象が起きているのかを学び、どのように質量とエネルギーが変化するのか計算しましょう。






