電気回路に抵抗が存在するとき、オームの法則を利用することで電圧・電流・抵抗の大きさを計算できます。ただ場合によっては、オームの法則に従わないケースがあります。このような抵抗を非オーム抵抗(非直線抵抗)といいます。
非オーム抵抗では、直線のグラフとはなりません。そのため、オームの法則を利用して計算することができません。
電流が流れることで発熱する場合、非オーム抵抗となります。物理では、電球が非オーム抵抗の例としてひんぱんに利用されます。
それでは、なぜオームの法則に従わないケースがあるのでしょうか。また、どのように非オーム抵抗での電圧や電流、抵抗の値を計算すればいいのでしょうか。非オーム抵抗の特徴やグラフ、計算方法を解説していきます。
もくじ
オームの法則に従わない抵抗が存在する
回路に抵抗\(R\)が存在する場合、電流\(I\)の値が大きくなると、それに伴って電圧\(V\)も大きくなります。オームの法則では\(V=RI\)となり、式を変形すると\(I=\displaystyle\frac{1}{R}V\)となります。
抵抗の値が一定の場合、\(\displaystyle\frac{1}{R}\)は定数です。そのためたて軸を\(I\)、横軸を\(V\)とすると、\(I=\displaystyle\frac{1}{R}V\)は直線グラフになります。一方で非オーム抵抗では、曲線のグラフになります。
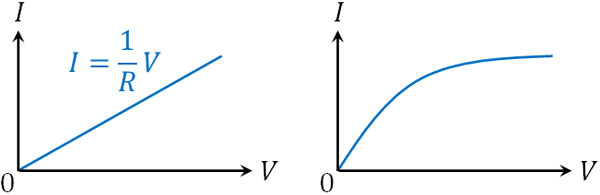
このグラフを見てわかる通り、非オーム抵抗では、電圧\(V\)を大きくしても電流\(I\)の値は少ししか変化しないとわかります。非オーム抵抗(非直線抵抗)では、いずれにしても曲線のグラフになります。
発熱があると非オーム抵抗(非直線抵抗)となる
それでは、どのような場合に非オーム抵抗となるのでしょうか。一般的な抵抗では、オームの法則に従います。一方で、電流が通ると熱くなる製品は非オーム抵抗となります。
電気が通ることによって熱くなる製品に電球があります。いまでは電流が流れても高熱になりにくい電球が利用されているものの、かつての電球(白熱電球など)は利用することで非常に高温になっていました。また電熱線を利用するなど、高温になる製品はたくさんあります。
なぜ、発熱する製品は非オーム抵抗になるのでしょうか。抵抗というのは、自由電子の流れにくさを表しています。電子が金属イオンに衝突することにより、電子の運動エネルギーが金属イオンの熱振動に利用されて発熱するのです。
低温の場合、金属イオンの振動は弱いです。この場合、自由電子はスムーズに金属内を移動できます。
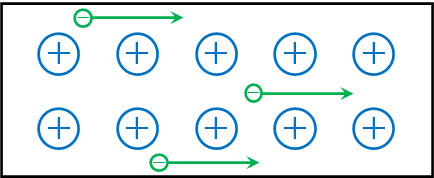
一方で発熱する製品では、熱によって金属イオンの振動が激しくなります。当然、金属イオンの振動が激しいほど自由電子は金属内を流れにくくなり、結果として抵抗がより大きくなります。
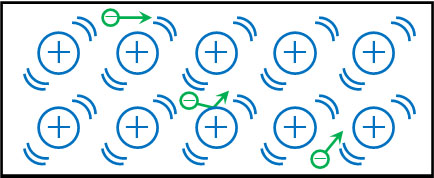
電圧を大きくしても、非オーム抵抗では発熱によって抵抗が大きくなり、電流の値が大きくなりにくいのです。非オーム抵抗(非直線抵抗)では、このように熱が関与しているのです。
非オーム抵抗の問題を解く場合、グラフとの交点を利用する
それでは、非オーム抵抗に関する問題をどのように解けばいいのでしょうか。非直線抵抗では、必ずグラフを利用しましょう。
非オーム抵抗のグラフには、電流\(I\)と電圧\(V\)を利用して曲線が記されています。この曲線に加えて、グラフに直線を書きましょう。その後、2つの線の交点を確認することで答えを得ます。
恐らく問題を解かないと、解き方を理解することはできません。そこで、以下の問題を解いてみましょう。
- 電球を含む回路あり、電圧は20V、抵抗は10Ωです。電球に電流\(I\)を流すとき、電球に加わる電圧\(V\)が下のグラフのようになるとき、電球に対する電流\(I\)と電圧\(V\)はいくらですか。
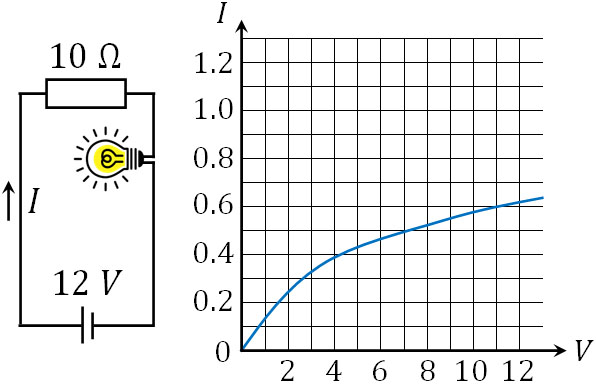
普通の抵抗の場合、オームの法則に従います。一方で電球については、非オーム抵抗となります。そこで電球による電圧降下(電位差)を\(V_1\)とするとき、回路を利用して式を作りましょう。キルヒホッフの法則より、以下のようになります。
- \(12=10I+V_1\)
そこで、この式を以下のように変形しましょう。
\(12=10I+V_1\)
\(10I=-V_1+12\)
\(I=-0.1V_1+1.2\)
こうして、傾きが-0.1、切片が1.2の直線となります。そこで、この直線をグラフに記入しましょう。
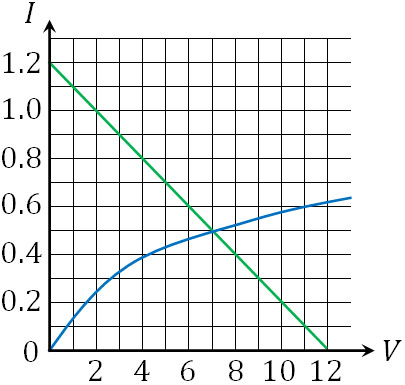
グラフを確認すると、電流\(I\)が0.5A、電圧\(V\)が7Vの場所で交わっています。そのため、0.5Aと7Vが正解です。
なぜ、2つの線の交点が答えになるのでしょうか。回路が成り立つためには、必ず\(12=10I+V_1\)となる必要があります。また、電球の特性が成り立つためには、グラフに存在する曲線を満たす必要があります。
つまり、2つの条件を満たす必要があります。交点であれば、回路の条件と電球の条件を満たすことができます。そのため、2つの線の交点が答えになるのです。
直接接続での非オーム抵抗
それでは、電球が直列接続で2つ存在する場合はどのように考えればいいのでしょうか。先ほどの問題について、まったく同じ性質の電球を利用して以下のように直列接続するとき、回路を流れる電流\(I\)と一つの電球に加わる電圧\(V\)を求めましょう。
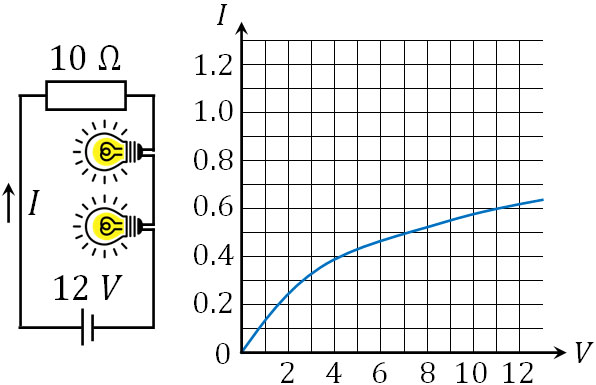
考え方は先ほどと同じです。回路全体の式を作りましょう。電球に加わる電圧を\(V_1\)とすると、以下のようになります。
\(12=10I+V_1+V_1\)
\(10I=-2V_1+12\)
\(I=-0.2V_1+1.2\)
こうして傾き-0.2、切片1.2の直線になるとわかります。そこで、以下のグラフを作りましょう。
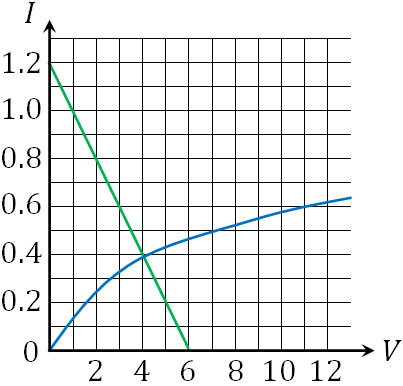
グラフの交点より、電流は0.4A、電圧は4Vになるとわかります。
並列接続での非オーム抵抗
次に、電球を並列接続する場合の非オーム抵抗を確認しましょう。先ほどと同じ電球を利用し、以下のように接続する場合、一つの電球に対する電流\(I\)と電圧\(V\)はいくらでしょうか。
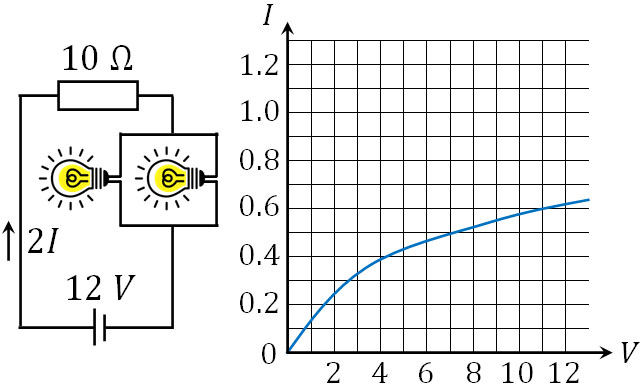
回路全体の式を作りましょう。電流はそれぞれの電球に対して半分ずつ流れます。そのため電球に電流\(I\)が流れる場合、一般的な抵抗に流れる電流は\(2I\)となります。
また電球は並列接続であるため、電位差に違いはありません。そこで電球に加わる電圧を\(V_1\)とすると、以下の式を作れます。
\(12=20I+V_1\)
\(20I=-V_1+12\)
\(I=-0.05V_1+0.6\)
直線は傾きが-0.05、切片が0.6となります。そのため、以下の直線を作りましょう。
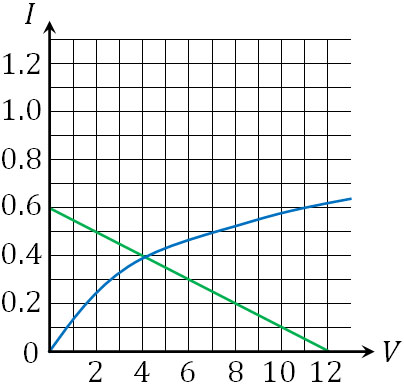
2つの線の交点を確認すると、電流は0.4A、電圧は4Vが正解であるとわかります。
グラフを利用して非オーム抵抗(非直線抵抗)の問題を解く
電気を利用した製品の中には、電流が流れることで高温になるケースがあります。発熱する電化製品を利用する場合、オームの法則に従いません。グラフを描いても、直線ではなく曲線になるのです。
この場合、オームの法則を利用して電圧や電流、抵抗を計算することはできません。一般的な抵抗とは異なり、抵抗の値は一定ではありません。発熱によって、抵抗の値が大きくなるのです。
そこで非オーム抵抗では、グラフを利用して電圧や電流を計算しましょう。回路全体に着目して式を作り、直線の式を得るのです。その後、グラフに直線を書き加えることで2つの線の交点を調べましょう。2つの線の交点が答えになります。
オームの法則を利用できないケースがあります。その場合、どのように電圧と電流を計算すればいいのか理解しましょう。






