すべての物体が受ける力に万有引力があります。ニュートンが万有引力の法則を発見したことで有名です。
万有引力の法則は主に宇宙空間での力学で利用されます。人間のように、軽い物体に働く万有引力の影響は非常に小さいです。そのため恒星や惑星、衛星のような大きい物体に対して万有引力の法則を利用するのです。
万有引力の法則では公式を利用します。そこで、公式が何を意味しているのか学びましょう。また万有引力の法則を学ぶとき、万有引力による位置エネルギーを習います。なぜ、万有引力による位置エネルギーがマイナスになるのか理解しましょう。
それでは、どのように公式を利用して万有引力を計算すればいいのでしょうか。万有引力の計算方法や公式の意味、万有引力による位置エネルギーがマイナスになる理由を含めて解説していきます。
もくじ
万有引力の法則と公式
2つの物体に働く引き合う力を万有引力といいます。質量\(m\)の物体と質量\(M\)の物体があり、2つの物体の距離が\(r\)のとき、2つの物体に働く万有引力(引き合う力)\(F\)は以下のように表すことができます。
- \(F=G\displaystyle\frac{mM}{r^2}\)
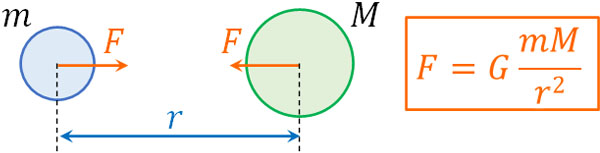
つまり2つの物体の質量をそれぞれかけた後、距離の2乗で割ることによって万有引力を得ることができます。なお\(G\)は定数であり、万有引力定数と呼ばれます。\(G\)の値は約6.67×10-11N·m2/kg2です。
それでは、50kgの人と体重60kgの人が1m離れているとき、二人の間で働く万有引力はいくらでしょうか。公式に値を当てはめると以下のようになります。
\(F=6.67×10^{-11}×\displaystyle\frac{50×60}{1^2}\)
\(F≒2.0×10^{-7}\)
二人の間で働く万有引力は\(2.0×10^{-7}\)Nであり、非常に小さい力です。万有引力はすべての物体で働くものの、日常生活で私たちが万有引力による影響を感じることはありません。
一方で地球は非常に質量の大きい物体であるため、万有引力による影響によって私たちは地球に引っ張られます。これが重力です。
万有引力の計算問題では円運動が関わる
重要なのは、万有引力の法則を利用して計算をするとき、円運動が関わることです。つまり、円運動の公式を覚えていなければ問題を解くことができません。
地球を含め、惑星の形は球です。そのためロケットを打ち上げるとき、ロケットは円運動をします。
人を乗せてロケットが月に行くにしても、ロケットは最初、地球の周りを動くので円運動をします。そのため、万有引力の法則を利用するときは円運動の公式を利用しましょう。円の半径を\(r\)、角速度を\(ω\)とすると、円運動で速さ\(v\)や加速度\(a\)を得る公式は以下になります。
- \(v=rω\)
- \(a=rω^2\)
この式を変形すると、加速度を以下のように表すことができます。
- \(a=\displaystyle\frac{v^2}{r}\)
それでは、万有引力の法則と円運動の公式を利用して練習問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 地球の半径を\(r\)、人工衛星の地表面からの高さを\(h\)、重力加速度を\(g\)とします。人工衛星の速さ\(v\)について、\(r\)、\(h\)、\(g\)を用いて表しましょう。
問題を解くため、図を描きましょう。地球の重さを\(M\)、人工衛星の重さを\(m\)、万有引力定数を\(G\)とします。
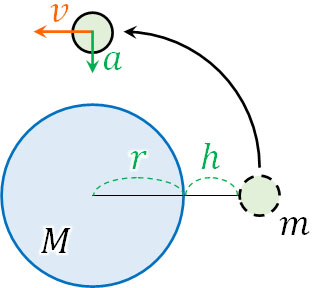
円運動している物体は中心に向かって力が働いています。人工衛星は地球の周囲を回っているため、地球の中心に向かって常に加速度\(a\)が加わっています。
なお人工衛星はどの物体とも触れていないものの、地球との間で万有引力を生じています。つまり人工衛星に生じている力(地球の中心方向へ加わる力)というのは、地球と人工衛星による万有引力と等しいです。
運動方程式より、\(F=ma\)です。前述の通り\(a=\displaystyle\frac{v^2}{r}\)(\(r\)は中心からの距離)であるため、人工衛星が円運動するとき、地球の中心に向かって加わっている力(向心力)\(F\)は以下のように表せます。
\(F=m\displaystyle\frac{v^2}{r+h}\)
地球の中心から人工衛星の距離は\(r+h\)であることに注意しましょう。なお人工衛星による向心力と「地球と人工衛星による万有引力」は等しいため、以下の運動方程式を作りましょう。
\(m\displaystyle\frac{v^2}{r+h}=G\displaystyle\frac{mM}{(r+h)^2}\)
\(v^2=\displaystyle\frac{GM}{r+h}\)
\(v=\sqrt{\displaystyle\frac{GM}{r+h}}\) (\(v>0\))
ただ答えの中に万有引力定数\(G\)が式に残っているため、万有引力定数を消しましょう。
人工衛星が仮に地表に存在する場合、重力によって加わる力は\(mg\)です。重力というのは、言い換えると万有引力\(G\displaystyle\frac{mM}{r^2}\)を指します。先ほどとは異なり、人工衛星は地表にあります。つまり地球の中心からの距離は\(r+h\)ではなく\(r\)であるため、以下の運動方程式を作りましょう。
\(mg=G\displaystyle\frac{mM}{r^2}\)
\(G=\displaystyle\frac{gr^2}{M}\)
そこで、先ほどの計算した式に\(G=\displaystyle\frac{gr^2}{M}\)を代入しましょう。
\(v=\sqrt{\displaystyle\frac{GM}{r+h}}\)
\(v=\sqrt{\displaystyle\frac{M}{r+h}×\displaystyle\frac{gr^2}{M}}\)
\(v=r\sqrt{\displaystyle\frac{g}{r+h}}\)
こうして、人工衛星の速さは\(v=r\sqrt{\displaystyle\frac{g}{r+h}}\)とわかりました。
万有引力による位置エネルギーの公式
万有引力を用いて計算するとき、運動方程式に加えて、力学的エネルギー保存則を利用できるようになりましょう。
宇宙では、ばねによる弾性エネルギーを考慮する必要はありません。その代わり、運動エネルギーと位置エネルギーを考慮しましょう。速さ\(v\)に加えて、位置エネルギーがわかれば力学的エネルギー保存則を利用できます。
質量\(m\)の物体が質量\(M\)の物体から距離\(r\)の場所にあるとき、質量\(m\)の物体の位置エネルギー\(U\)は以下の公式によって表されます。
- \(U=-G\displaystyle\frac{mM}{r}\)
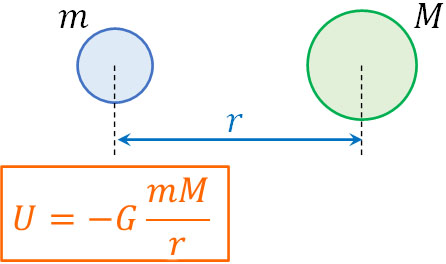
力学的エネルギー保存則を習うとき、位置エネルギーは\(mgh\)と教わったと思います。万有引力で位置エネルギーを利用する場合、\(mgh\)ではなく\(-G\displaystyle\frac{mM}{r}\)を用いて式を作りましょう。
位置エネルギーがマイナスであることは問題がない:無限遠でのエネルギー
なお万有引力による位置エネルギーを学ぶとき、「なぜ位置エネルギーにマイナスが加わっているのか」と疑問に思います。
どこを基準にするのかによって位置エネルギーが変化します。例えばあなたがビルの屋上に立って質量\(m\)のボールを自由落下させる場合、ビルの屋上から下へ距離\(h’\)の位置にあるボールの位置エネルギーは\(-mgh’\)です。

一方、ビルの屋上ではなく、地上を基準とする場合、地上からボールまでの距離が\(h\)なのであれば、ボールの位置エネルギーは\(mgh\)です。
位置エネルギーはどこを基準にするのかによって、符号がプラスになったりマイナスになったりします。そのため、位置エネルギーがマイナスであることに何か問題があるわけではありません。
それでは、万有引力ではどこを位置エネルギーの基準としているのでしょうか。万有引力では、一般的に無限遠∞(むげんえん:無限に遠い場所)を基準点として0にしている場合がほとんどです。無限遠を基準にして位置エネルギーを0にする場合、必ず位置エネルギーがマイナスになるので計算が楽です。
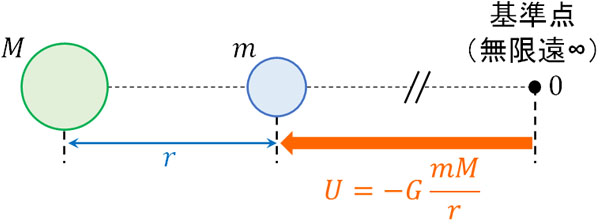
なお位置エネルギーの基準点を無限遠∞ではなく、ほかの場所に設定することも可能です。この場合、位置エネルギーはプラスになったり、マイナスになったりします。
ただ地球の中心を位置エネルギーの基準にする場合、万有引力による位置エネルギーが無限大に大きくなるため都合が悪いです。宇宙は広いため、地球から離れるに従って位置エネルギーは無限に大きくなり、計算するときに不都合です。
そこで無限遠を位置エネルギーの基準にして、無限遠よりも近い場所の位置エネルギーを計算します。これによって位置エネルギーが無限大に大きくなるのを避け、力学的エネルギー保存則を利用して計算できるようにするのです。無限遠を位置エネルギーの基準にするのはこうした理由があります。
積分を用いる万有引力での位置エネルギーの導出
それでは、どのように万有引力による位置エネルギーの公式を導き出すのか学びましょう。積分を利用するため、この部分を読み飛ばし、公式である\(U=-G\displaystyle\frac{mM}{r}\)を暗記しても問題ありません。
ただ万有引力による位置エネルギーの公式を出すとき、高校数学で学ぶ積分の初歩を学んでいれば理解できます。積分を学んだことがある場合、全員が万有引力による位置エネルギーの公式を導出できます。
位置エネルギーというのは、要は仕事と意味が同じです。仕事\(W\)は力の大きさ\(F\)と距離\(x\)のかけ算により、\(W=Fx\)によって得られます。
例えば\(mg\)の力(重力)をもつ物体を高さ\(h\)の場所にもっていくため、位置エネルギーは\(mgh\)によって計算できます。これはつまり、横軸を距離\(x\)、たて軸を力の大きさ\(F\)とするとき、面積を計算しているのと意味は同じです。
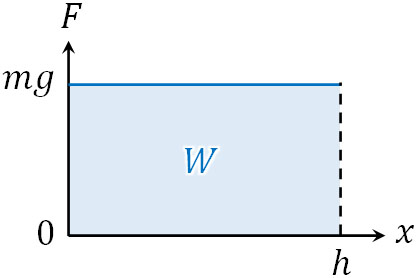
そこで同じように、万有引力について仕事(位置エネルギー)を計算しましょう。
地球(質量\(M\))から\(r\)の位置にある質量\(m\)の物体には、\(F=G\displaystyle\frac{mM}{r^2}\)の引力が働いています。そこで、\(F=G\displaystyle\frac{mM}{r^2}\)に逆らいながら無限遠までもっていく場合の仕事を計算しましょう。
ただ万有引力の大きさは地球との距離\(r\)によって変化します。無限遠に近づくほど万有引力は小さくなります。つまり同じ距離を移動するにしても、地球から遠くなるに従って仕事量が小さくなります。
そこで積分をしましょう。\(r\)から無限大までの\(x\)軸について、\(F=G\displaystyle\frac{mM}{r^2}\)によって囲まれる面積を計算するのです。これにより、万有引力による仕事(位置エネルギー)を計算できます。
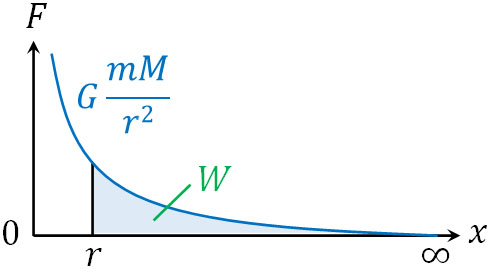
そこで、以下の計算をしましょう。
\(W=\displaystyle \int_{r}^{\infty} G\displaystyle\frac{mM}{r^2} dr\)
\(=GmM \displaystyle \int_{r}^{\infty} \displaystyle\frac{1}{r^2} dr\)
\(=GmM \displaystyle \int_{r}^{\infty} r^{-2} dr\)
\(=GmM \left[ \displaystyle\frac{1}{-2+1}r^{(-2+1)} \right]_r^{\infty}\)
\(=GmM \left[ -\displaystyle\frac{1}{r} \right]_r^{\infty}\)
\(=GmM \left(0+\displaystyle\frac{1}{r}\right)\)
\(=G\displaystyle\frac{mM}{r}\)
こうして、地球からの距離\(r\)から無限遠まで物体をもっていくために必要な仕事は\(W=G\displaystyle\frac{mM}{r}\)と計算できました。
なお前述の通り、基準点は無限遠です。そのため\(r\)の位置にある物体は無限遠に対して、エネルギーが\(G\displaystyle\frac{mM}{r}\)の分だけ低くなります。そのため、\(U=-G\displaystyle\frac{mM}{r}\)となります。
万有引力による位置エネルギーがマイナスになると説明している教科書は多いものの、理由は詳しく解説されていません。そこで、なぜ万有引力による位置エネルギーがマイナスになり、どのように位置エネルギーの公式を導出するのか理解しましょう。
力学的エネルギー保存則を利用する万有引力での練習問題
それでは、万有引力による位置エネルギーを利用して計算問題を解きましょう。位置エネルギーを利用するというのは、力学的エネルギー保存則を利用することを意味します。例えば、以下の問題の答えは何でしょうか。
- 地球の半径を\(r\)、重力加速度を\(g\)とします。地表から打ち上げた物体が再び戻ってこないために必要な初速度\(v_0\)について、\(r\)と\(g\)を利用して求めましょう。
物体を打ち上げた後の速さを\(v\)とするとき、力学的エネルギー保存則を利用すると以下の式を作ることができます。
\(\displaystyle\frac{1}{2}mv_0^2-G\displaystyle\frac{mM}{r}=\displaystyle\frac{1}{2}mv^2\)
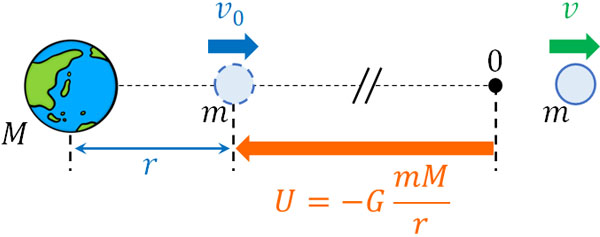
無限遠に物体が存在する場合、位置エネルギーはゼロです。このときの速さは\(v\)であるため、物体は運動エネルギーのみ保有しています。一方、地表に存在する場合は運動エネルギーとマイナスの位置エネルギーの両方をもっています。
また位置エネルギーよりも高い運動エネルギーで打ち上げると、無限遠のときに物体は速さ\(v\)で地球から遠ざかるため、地表に戻ってくることはありません。
無限遠のときに物体が速さ\(v\)となる条件は先ほどの式より以下のようになります。
\(\displaystyle\frac{1}{2}mv_0^2-G\displaystyle\frac{mM}{r}=\displaystyle\frac{1}{2}mv^2≧0\)
つまり、以下の計算をすればいいとわかります。
\(\displaystyle\frac{1}{2}mv_0^2-G\displaystyle\frac{mM}{r}≧0\)
\(v_0^2≧2G\displaystyle\frac{M}{r}\)
\(v_0≧\sqrt{\displaystyle\frac{2GM}{r}}\) (\(v_0>0\))
なおほかの練習問題で解説した通り、地表での重力による影響\(mg\)と万有引力より、以下の運動方程式が成り立ちます。
\(mg=G\displaystyle\frac{mM}{r^2}\)
\(G=\displaystyle\frac{gr^2}{M}\)
そこで、\(G=\displaystyle\frac{gr^2}{M}\)を代入しましょう。
\(v_0≧\sqrt{\displaystyle\frac{2GM}{r}}\)
\(v_0≧\sqrt{2gr}\)
こうして初速度が\(v_0≧\sqrt{2gr}\)のとき、物体は再び地表に戻ることなく、宇宙空間を進むと計算できました。
万有引力の公式を覚え、位置エネルギーの概念を理解する
すべての物体に万有引力が存在するものの、人間を含め軽い物体同士で万有引力を感じることはありません。そのため、万有引力の法則は惑星や衛星、彗星など宇宙空間で利用されます。
万有引力を計算するとき、2つの物体の質量をかけ、距離の2乗で割りましょう。これにより、2つの物体に働く力を計算できます。
また万有引力を学ぶとき、位置エネルギーを利用して式を作らなければいけないケースがたくさんあります。力学的エネルギー保存則を利用して式を作るのです。このとき、なぜ位置エネルギーがマイナスになるのか理解しましょう。
宇宙が関わる学問に万有引力があります。軌道の計算やロケットの速度、人工衛星の打ち上げではこうした知識が必要になります。力学の計算は宇宙で必須であり、これらの計算を行えるようになりましょう。