電圧を加えることにより、導体に電流が流れます。このとき、磁場が存在する場合はどのような現象が起こるのでしょうか。
磁場が存在する状態で導体に電流を流す場合であっても、電流は流れます。ただ磁場がある場合、磁場とは垂直な方向に電圧を生じます。つまり、電源による電圧とは別に電圧を生じるのです。これをホール効果といいます。
ホール効果の仕組みは複雑です。そのためホール効果やホール電圧を学ぶとき、どのような現象が起こっているのか順に確認しなければいけません。
それでは、なぜ磁場があると新たな電圧を生じるのでしょうか。また、ホール効果に関する問題をどのように解けばいいのでしょうか。磁場と電流によって新たな電圧を生じる原理を解説していきます。
もくじ
導体内での電流と電子、ローレンツ力の関係
自由電子が動くことによって電流が流れる事実は既に知っていると思います。電子が動くことによって電流が発生するのです。そこで、導体に電流が流れている場面を考えましょう。
このとき磁場(磁束密度)があると、磁場は電流に対して力を加えます。例えば下図の場合、フレミングの左手の法則を利用すると、力の向きがわかります。
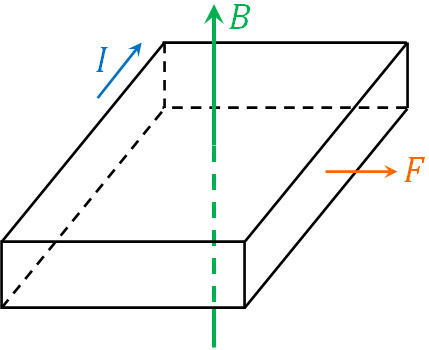
なお前述の通り、電流と電子の向きは逆です。そのため負に荷電している粒子(電子)に着目する場合、電流とは逆向きに粒子が動いています。このとき、電流に加わる力とローレンツ力(粒子に加わる力)について、当然ながら向きは同じです。そのため、以下のような図になります。
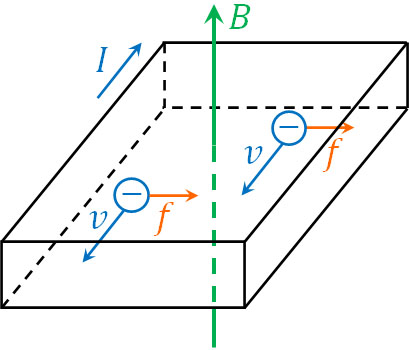
このように、ローレンツ力によって電子は力を受けます。
自由電子は一方に集まり、電荷の偏りにより電場を生じる
磁場(磁束密度)があるとローレンツ力が働くため、電子は導体内の一方に移動します。例えば下図のように、側面1よりも、側面2で自由電子の数が多くなります。
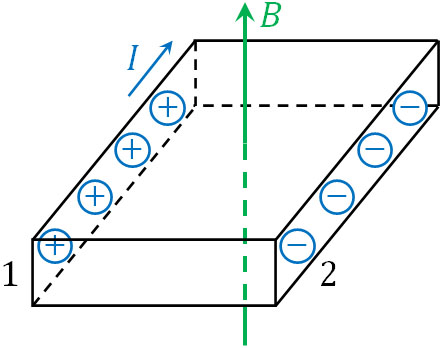
側面2で電子が多い場合、側面2は負に荷電します。一方、側面1では電子が少なくなるため、正に荷電します。このように、電荷の偏りを生じるのです。つまり、側面1と側面2の間には電位差(電圧)を生じます。
このとき生じる電圧をホール電圧といいます。図を確認すればわかる通り、ホール電圧は電流と磁場の両方向に対して垂直です。
また、この現象をホール効果といいます。磁場が存在するとき、電流を流すことによって、電流と磁場に対して垂直方向に新たな電圧(ホール電圧)を生じる現象がホール効果です。電源による起電力とは別に、導体の側面に起電力(ホール電圧)を生じるのです。
ローレンツ力と電場による力がつり合う
それでは、電場が存在する状態で自由電子が動くと、ローレンツ力によってすべての電子が側面2へ移動するのでしょうか。実際には、そのような現象は起こりません。
正電荷と負電荷がある場合、正電荷から負電荷に向かって電場を生じます。電子はマイナスの電荷を帯びているため、電場の影響を受けて正電荷へ引き寄せられます。電子の電気量を\(-e\)、電場を\(E\)とすると、電子が電場から受ける力は\(F=eE\)です。
ただ先ほど述べた通り、磁場の影響によって電子にはローレンツ力が働きます。ローレンツ力\(f\)は\(f=evB\)です。
電場によって側面1へ移動するための力が働き、ローレンツ力によって側面2へ移動するための力が働きます。そのため時間が経過すると、電場による力\(F\)とローレンツ力\(f\)がつり合います。
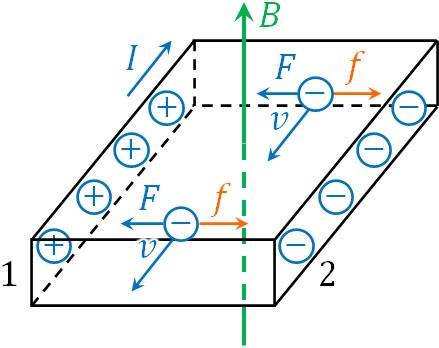
つまり、以下の状態となっています。
\(F=f\)
\(eE=evB\)
\(E=vB\)
ホール効果によって電場の強さが\(E=vB\)となると、電場による力とローレンツ力がつり合い、電子は導体内をまっすぐ進みます。
練習問題を解き、ホール効果を理解する
それでは、練習問題を解くことによってホール効果への理解を深めましょう。以下の問題の答えは何でしょうか。
- 下図のように横の長さ\(a\)、たての長さ\(b\)の長方形を断面とする導体に電流\(I\)が流れています。また、電流\(I\)の向きと磁束密度\(B\)の向きは図に記している通りです。なお、電子の電気量を\(-e\)、電子の速さを\(v\)、単位体積(1m3あたり)に存在する電子数を\(n\)とします。
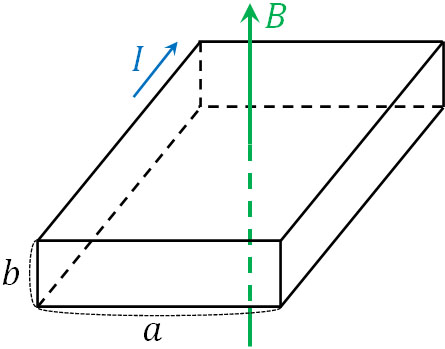
- 電流の大きさを求めましょう。
- \(v\)と\(B\)を用いてホール電圧を表しましょう。
- \(n\)を用いてホール電圧を表しましょう。
1) 電流の大きさを求めましょう
電流の定義を学んでいるはずなので、容易に答えを出せると思います。経過時間を\(t\)とすると、\(t\)秒で電子が進む距離は\(tv\)[m]です。断面積は\(ab\)[m2]であるため、\(t\)秒で電子が進む体積は\(abtv\)[m3]です。
そのため、一つの電子による電気量\(Q\)は\(eabtv\)[C]です。また単位体積あたりに存在する電子数は\(n\)なので、合計の電気量は\(enabtv\)[C]です。
電流の定義より、1秒で得られる電気量が電流なので\(I=\displaystyle\frac{Q}{t}\)です。そのため、電流は\(I=enabv\)[A]です。
2) \(v\)と\(B\)を用いてホール電圧を表しましょう
先ほど解説した通り、\(E=vB\)となります。そこで、この式をさらに変形しましょう。ホール電圧を\(V\)とすると、電場\(E\)と距離\(a\)の関係は以下のようになります。
\(V=aE\)
\(E=\displaystyle\frac{V}{a}\)
電気を学んでいる場合、この関係を何度も利用していると思います。一様な電場\(E\)は距離\(d\)(問題文の\(a\)に該当)と電圧(高さ)\(V\)に対する傾きを表します。
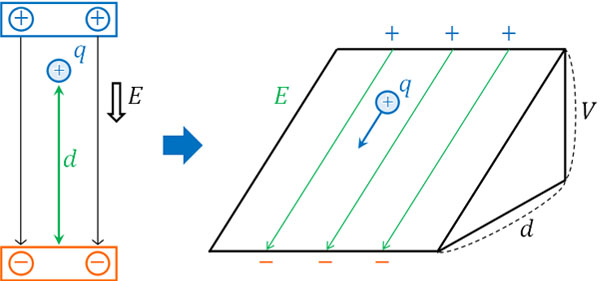
そこで、\(E=\displaystyle\frac{V}{a}\)を\(E=vB\)に代入しましょう。
\(E=vB\)
\(\displaystyle\frac{V}{a}=vB\)
\(V=avB\)
こうして、\(V=avB\)であるとわかりました。
3) \(n\)を用いてホール電圧を表しましょう
次に、ほかの数式によってホール電圧を表しましょう。\(I=enabv\)であるため、\(v=\displaystyle\frac{I}{enab}\)です。そこで、\(v=\displaystyle\frac{I}{enab}\)を\(V=avB\)に代入しましょう。
\(V=avB\)
\(V=aB×\displaystyle\frac{I}{enab}\)
\(V=\displaystyle\frac{IB}{enb}\)
こうして、ホール電圧は\(V=\displaystyle\frac{IB}{enb}\)とわかりました。
ホール効果の詳細を知り、ホール電圧を計算する
ホール効果が発生するメカニズムは複雑です。そのためホール効果を言葉で説明しても、理解するのは難しいです。そこで磁場が存在し、かつ自由電子が導体内を動くとき、どのような現象が起こるのか一つずつ確認しましょう。
導体内を電子が動く場合、磁場が存在するとローレンツ力が発生します。これによって電子に偏りを生じ、電荷が発生します。こうして生じる新たな起電力がホール電圧です。
また電荷の偏りによって電場が発生し、電場による力とローレンツ力がつり合います。これにより、電子はまっすぐに導体内を進みます。
なおホール効果が起きているとき、ホール電圧を計算できるようになりましょう。「ホール効果によってどのような現象が起きているのか」について原理を学べば、ホール電圧の計算が可能になります。






