金属元素と金属元素は互いに結合を作ります。これを金属結合といいます。金属結合というのは、共有結合やイオン結合と同じ化学結合の一種です。金属結合をするため、金属は一つの塊として存在できるのです。
化学結合の一つであるため、金属結合には独自の特徴があります。金属は電気を通すことができますし、物理的に伸ばすこともできます。これは、金属結合の特徴です。
また金属結合している場合、金属原子が規則正しく配列していることになります。これを金属結晶といいます。このとき、どのように原子が整列しているのかによって金属結晶の種類が異なります。
金属は私たちの身近に存在しており、金属結合を学ぶことで金属の性質をより深く理解できるようになります。そこで、化学で学ぶ金属結合や金属結晶について解説していきます。
もくじ
金属原子は金属結合によって結合している
通常、物質が原子のみの状態で存在することはありません。例えば酸素の場合、1つの酸素原子が存在することはなく、必ず分子(またはイオン)で存在します。具体的には、酸素分子(O2)として存在することによって最外殻電子が8になり、安定状態となります。
一方で元素によっては、最外殻電子を8にする必要がないケース(オクテット則を満たさなくても問題ないケース)があります。この例の一つが金属元素です。金属元素の場合、金属結合を作ることができるので金属単体で存在できるのです。
例えば鉄(Fe)や銅(Cu)、アルミニウム(Al)、金(Au)、銀(Ag)、プラチナ(Pt)などの金属というのは、酸素原子(O)や塩素原子(Cl)などのように、その他の原子と結合しなくても、金属単体で存在できることは多くの人が理解できると思います。
ほかの原子と電子を共有していないにも関わらず原子単体で存在できるのは、前述の通りこれらの元素が金属結合を形成できるからなのです。
電子は共有され、自由電子として自由に動ける
すべての原子は最外殻電子が8(水素原子の場合は最外殻電子が2)の状態で安定となります。つまり、必ずオクテット則を満たさなければいけません。
ただ金属結合の場合、金属元素全体で電子を共有し、最外殻電子は原子核を離れて自由に動き回れるという性質があります。そのため金属結合を形成すれば、電子はオクテット則を気にする必要がありません。
また価電子が金属全体で共有されるため、前述の通り電子は金属内を自由に動き回ることができます。この電子を自由電子といいます。
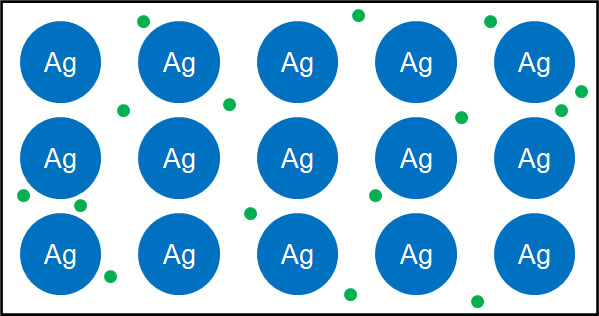
自由電子がたくさん存在するため、金属は電気を通します。通常、分子が電気を通さないのは電子を手放さないからです。一方で金属の場合、自由電子が大量に存在するため電子が動くのは容易であり、電気が流れるのです。
金属結合でつながっている場合、金属原子は電子を失い、すべて陽イオンとなります。またすべての陽イオン(金属原子)によって、電子を共有します。このように、ほかの化学結合とは異なる性質をもつのが金属結合です。
電気伝導性・熱伝導性が高く、展性・延性がある
私たちの身の回りにある金属を見ればわかりますが、金属には特有の光沢があります。これは自由電子が存在することによって起こる現象です。自由電子に光が当たることで可視光のほとんどが反射され、これによって金属光沢を生じるのです。

自由電子があるため、前述の通り金属は電気を通します。また熱は振動によって伝わり、通常は原子が振動することによって熱が伝わります。一方で自由電子をもつ場合、自由電子の振動によって熱を伝えることもできます。そのため、金属は熱が伝わりやすいです。
金属で電気伝導性や熱伝導性に優れるのは自由電子があるからなのです。
また金属では、圧縮したときに変形する能力(展性)や伸ばすときに変形する能力(延性)があります。共有結合している分子やイオン結合している物質の場合、当然ながら電子の動きは制限されます。分子から電子が離れるというのは、結合が壊れることを意味します。
一方で金属結合の場合、結合に関与している電子は全体で共有されており、自由に動くことができます。そのため、外力が加わるとき金属は変形しやすいのです。
金属結合での結晶構造:金属結晶の結晶格子と単位格子
金属は私たちの身の回りに存在するため、金属結合の性質を理解するのは難しくありません。ただ化学で金属結合を学ぶとき、同時に金属結晶の構造を習います。
金属結合によって金属元素が連なるとき、規則正しく配列する必要があります。これを金属結晶といいます。金属原子がどのように配列するのかによって、複数の種類に分かれます。結晶について、原子の空間的な配列を結晶格子といいます。
また、結晶格子の最小単位を単位格子といいます。単位格子は最小単位であるため、単位格子が何度も繰り返されることによって金属結晶となります。
体心立方格子、面心立方格子、六方最密構造の内容
それでは、金属結晶の結晶格子にはどのような種類があるのでしょうか。金属結晶の結晶格子には、以下の3種類があります。
- 体心立方格子
- 面心立方格子
- 六方最密構造
結晶格子の形や特徴は私たちにとって馴染みがありません。ただ化学で問題が出されるとき、単位格子の特徴を覚えていないと問題を解けません。そこで、それぞれの内容を確認していきましょう。
・体心立方格子
立方体について、それぞれの頂点と中心に原子が配置されている結晶構造を体心立方格子といいます。
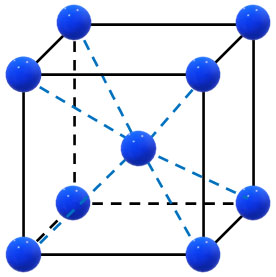
立方体の中心に原子があり、その周りを取り囲むように原子が存在することになります。
・面心立方格子
面心立方格子では、それぞれの頂点と面の中心に原子が存在します。
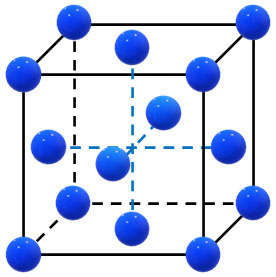
体心立方格子のように、立方体の中心に原子は存在しません。その代わり、面の中心に原子が存在することになります。
・六方最密構造
体心立方格子や面心立方格子に対して、六方最密構造は複雑な構造になっています。以下が六方最密構造です。
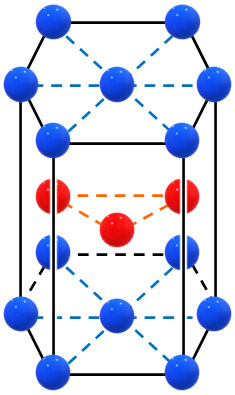
体心立方格子と面心立方格子の両方が組み合わさることによって六方最密構造になります。
なお六方最密構造の注意点として、単位格子を間違えないようにしましょう。六方最密構造の場合、以下の部分が単位格子になります。
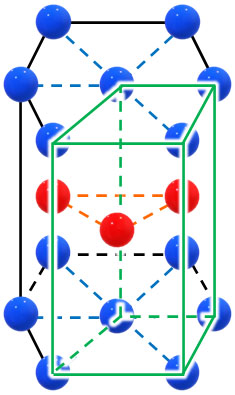
六角柱のうち、3分の1が単位格子です。六角柱全体が単位格子ではない点に注意しましょう。
結晶格子で重要な要素
なお化学では、これらの結晶格子を利用して問題が出されます。問われる内容は以下になります。
- 配位数
- 単位格子に存在する原子の数
- 単位格子一辺の長さと原子半径
- 充填率
そこで、これらの項目に対して答えられるようにしましょう。
配位数や単位格子に存在する原子の数、原子半径の計算
まず、配位数や単位格子に存在する原子の数、原子半径を計算しましょう。配位数とは、一つの原子に着目するとき、いくつの原子と接しているのかを指します。
・体心立方格子
結晶格子では、立方体を基準に考えましょう。立方体からはみ出ている部分をカットする必要があり、例えば体心立方格子では以下のようになります。
真ん中にある原子に着目すると、接している原子の数は8です。そのため、配位数は8です。また体心立方格子に存在する原子の数については、以下のように計算できます。
\(1+\displaystyle\frac{1}{8}×8=2\)
こうして、単位格子に存在する原子の数は2とわかりました。
また原子の半径を計算するとき、単位格子の一片の長さを\(a\)、原子半径を\(r\)としましょう。このとき、原子が接している部分に着目すると以下の図を作れます。
たての長さ(一辺の長さ)は\(a\)です。また、三平方の定理を利用して正方形の対角線の長さを計算すると\(\sqrt{2}a\)になります。横の長さが\(\sqrt{2}a\)であるため、上図での対角線の長さは\(\sqrt{3}a\)です。
それに対して、半径\(r\)が4つ存在するため、長方形の対角線の長さは\(4r\)です。そのため、以下のように原子半径を計算できます。
\(4r=\sqrt{3}a\)
\(r=\displaystyle\frac{\sqrt{3}}{4}a\)
・面心立方格子
次に面心立方格子の配位数や単位格子に存在する原子の数、原子半径を確認していきましょう。面心立方格子では以下の図で考えます。
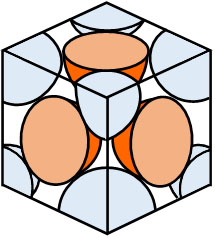
配位数については、以下のように2つの単位格子を利用すると理解しやすいです。
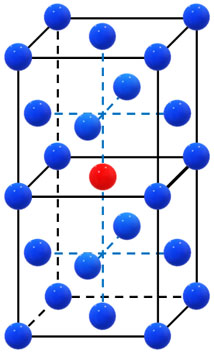
赤色の原子に着目すると、12個の原子と接していることがわかります。そのため、面心立方格子での配位数は12です。
また単位格子に存在する原子の数について、以下のように計算しましょう。
\(\displaystyle\frac{1}{2}×6+\displaystyle\frac{1}{8}×8=4\)
こうして、単位格子の中に4つ分の原子が含まれているとわかります。
それでは、原子半径についてはどのように計算すればいいのでしょうか。単位格子の一片の長さを\(a\)、原子半径を\(r\)とするとき、正方形の図を利用して半径を計算しましょう。
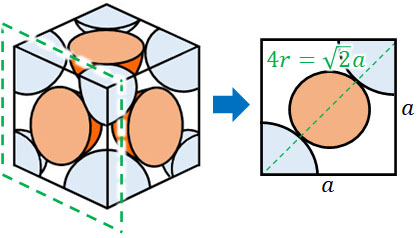
一辺が\(a\)であるため、正方形の対角線の長さは\(\sqrt{2}a\)です。また半径\(r\)が4つあるため、以下の計算によって半径を出すことができます。
\(4r=\sqrt{2}a\)
\(r=\displaystyle\frac{\sqrt{2}}{4}a\)
・六方最密構造
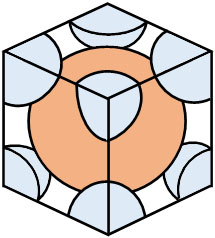
六方最密構造で配位数を数えるとき、以下のように2つの単位格子をつなぎましょう。
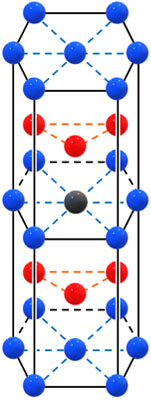
黒色の原子に着目すると、12個の原子と隣接していることがわかります。そのため、六方最密構造の配位数は12です。
また単位格子に存在する原子の数について、上面にある原子は1.5個、中にある原子は3個、下面にある原子は1.5個です。つまり、合計6個の原子が六角柱に存在します。
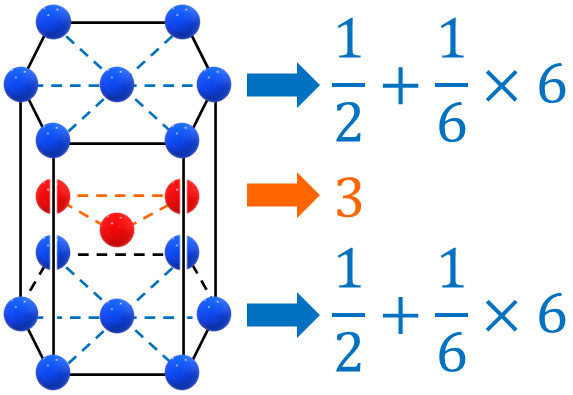
なお前述の通り、六方最密構造の単位格子は3分の1です。そのため、単位格子に存在する原子の数は2です。
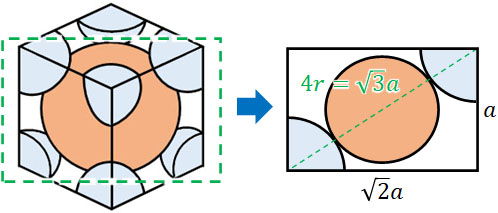
原子半径については、単位格子の一片の長さを\(a\)、原子半径を\(r\)とするとき、以下の図を利用することによって計算できます。
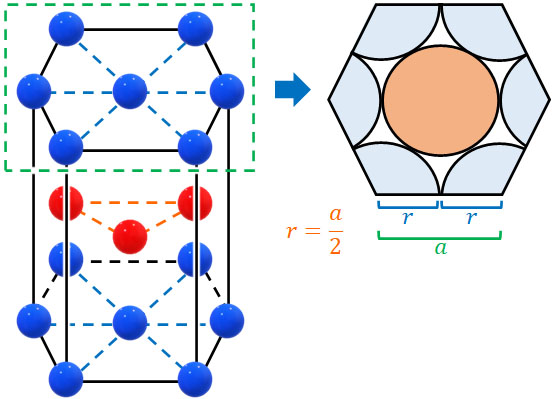
こうして、六方最密構造の原子半径は\(r=\displaystyle\frac{a}{2}\)とわかります。
結晶格子の充填率の概念
結晶格子について、どれだけ原子で満たされているのかを表すのが充填率(じゅうてんりつ)です。原子と原子の間には、当然ながらすき間があります。充填率というのは、どれだけすき間がなく原子が埋まっているのかを指します。
充填率については、原子の体積に対して、結晶格子の体積で割ることによって計算できます。実際に計算をすると以下のようになります。
- 体心立方格子:充填率68%
- 面心立方格子:充填率74%
- 六方最密構造:充填率74%
面心立方格子は別名で立方最密構造と呼ばれます。そのため、面心立方格子と六方最密構造で最も充填率が高くなります。
金属には特有の性質がある
化学を学ぶとき、共有結合とイオン結合はメインとなる化学結合です。それに対して、金属結合は共有結合やイオン結合ほど重要ではありません。
ただ私たちの周りには多くの金属が存在しており、金属結合を学ぶことによって、これらの性質をより深く理解できます。金属がもつ特徴というのは、金属結合によって自由電子が存在するために起こります。
また金属結晶の種類も学びましょう。金属結晶には体心立方格子、面心立方格子、六方最密構造の3種類があります。これら結晶格子の形を覚えましょう。また配位数や単位格子に存在する原子の数、原子の半径を計算できるようになるといいです。
特徴的な結合の一つが金属結合です。また、金属結合によって作られるのが金属結晶です。これらの性質を理解しましょう。