負の数を学ぶとき、多くの人が混乱します。異なる符合の掛け算や割り算をすると、符合が変わるからです。さらにいうと、マイナスとマイナスの掛け算をすると、符合はプラスになります。なぜ、そのようになるのでしょうか。
この理由を説明できる人はほとんどいません。ただ、中学校の数学を理解するためには事前に疑問を解決する必要があります。
掛け算での符合を理解すれば、割り算や累乗だけでなく、四則計算などの応用問題を解けるようになります。
負の数の計算について、概念を理解できず難しいと感じる人が多いです。そこで、マイナスの掛け算で符合が変わる理由や問題の解き方を解説していきます。
もくじ
符合の違いにより、掛け算はプラスまたはマイナスになる
プラスの数だけを勉強する場合、マイナスの数を考慮する必要がありません。ただ中学数学では、負の数を取り扱わなければいけません。
数学には掛け算(乗法)と割り算(除法)があります。掛け算をするとき、どのような符号を利用するのかによって、答えの符合が変化します。掛け算では、以下のようになります。
- 正の数\((+)×\)正の数\((+)=+\)
- 負の数\((-)×\)正の数\((+)=-\)
- 正の数\((+)×\)負の数\((-)=-\)
- 負の数\((-)×\)負の数\((-)=+\)
4つも覚えなければいけないのかと考える人がいるかもしれません。ただ、これを覚える必要はありません。以下のようになります。
- 同じ符合の掛け算:\(+\)になる
- 異なる符合の掛け算:\(-\)になる
例えば、\(4×-3=-12\)です。異なる符合の掛け算だからです。一方で\(-4×-3=12\)です。同じマイナスの符合同士の掛け算だからです。
ただ、なぜ正の数と負の数を掛けると、答えはマイナスになるのでしょか。また、なぜ負の数と負の数を掛けると、答えはプラスになるのでしょうか。この理由を正しく説明できる人はほとんどいないため、この疑問を解決していきます。
プラスとマイナスによる掛け算(乗法)が成り立つ理由
掛け算(乗法)をするとき、プラスとマイナスの答えがなぜマイナスになるのでしょうか。この疑問を最初に解決しましょう。
一般的には、この疑問を解決するときは速さ・時間・距離で考えます。以下の公式が存在します。
- 速さ \(×\) 時間 \(=\) 距離
例えば、1km/h(時速1km)の速さで歩き、3時間が経過すると、3kmの距離を歩いていることになります。ここから、正の数同士の掛け算が成立すると分かります。
・異なる符合で答えがマイナスになる理由
それでは、なぜ異なる符合を利用すると答えがマイナスになるのでしょうか。0(ゼロ)は基準点を表します。またプラスの符合だけで計算する場合、将来のみを考えることになります。しかし実際には、過去も存在します。
歩いた距離については、以下のような図を作ることができます。
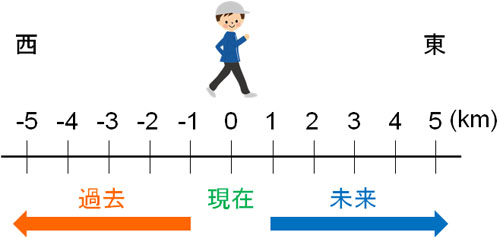
このとき、-1km/h(時速-1km)の速さで歩き、3時間が経過すると、どこにいるでしょうか。時速-1kmで歩くとは、上図でいういと、西に向かって時速1kmで歩いていることを意味します。西に向かって歩き、3時間が経過すると、-3kmの場所にいます。
- 時速\(-1km×3\)時間\(=-3km\)
また、1km/h(時速1km)の速さで歩き、-3時間が経過すると、どこにいるでしょうか。-3時間が経過するとは、3時間前のことを意味しています。東に向かって時速1kmで歩くとき、3時間前は-3kmの場所にいます。
- 時速\(1km×-3\)時間\(=-3km\)
このように考えると、なぜ正の数と負の数を掛けると、答えがマイナスになるのか理解できるようになります。
負の数と負の数を掛けると、プラスになる理由
それに対して、負の数と負の数を掛けるとなぜプラスになるのでしょうか。先ほどと同じように、速さ・時間・距離の関係で考えてみましょう。-1km/h(時速-1km)の速さで歩き、-3時間が経過したら、どこにいるでしょうか。
-1km/h(時速1km)の速さで歩くとは、西に向かって歩いていることを意味しています。また-3時間が経過するとは、3時間前のことを意味します。
西(マイナス)に向かって歩いている場合、3時間前では、+3km(東に3km)の場所にいることになります。
- 時速\(-1km×-3\)時間\(=+3km\)
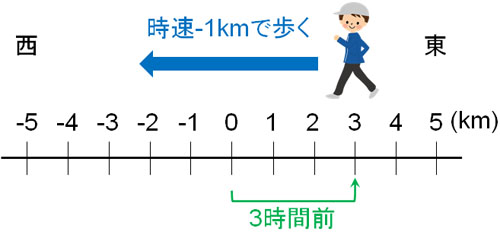
このような考え方によって、なぜマイナスとマイナスの掛け算をすると、答えがプラスになるのか分かります。
割り算(除法)も同じく符合が変化する
ここまで、掛け算について解説しました。それでは、割り算(除法)はどうなるのでしょうか。
割り算については、掛け算とまったく同じように考えます。つまり同じ符合同士の割り算では、答えはプラスの符合になります。一方で異なる符合の割り算では、答えはマイナスの符合になります。
- 同じ符合の割り算:\(+\)になる
- 異なる符合の割り算:\(-\)になる
この理由としては、掛け算も割り算も同じだからです。例えば、1km/h(時速1km)の速さで3時間歩くと、3kmを歩くことになります。
- 時速\(1km×3\)時間\(=3km\)
それでは、3kmの距離を3時間で歩いている場合、時速はいくらでしょうか。計算式と答えは以下のようになります。
- \(3km÷3\)時間\(=\)時速\(1km\)
このように、掛け算は割り算に変化させることができます。
例えば分数の割り算では、上下を逆にすることで、掛け算に直した式にすることができます。これは、掛け算と割り算は変化させることができるからです。掛け算と割り算は同じ性質です。そのため割り算(除法)での符合の変化は、掛け算と同じになります。
マイナスが偶数または奇数なのかで符合が変わる
ただ数学の計算をするとき、2つの数字だけの計算をすることは稀です。多くの場合、複数の数字の掛け算または割り算をします。いくつもの正の数や負の数を掛ける場合、符合はどのようになるのでしょうか。
この問題について、掛け算(または割り算)をするときマイナスの数が偶数であれば、答えの符合はプラスになります。それに対して、掛け算(または割り算)をするときマイナスの数が奇数であれば、答えの符合はマイナスになります。
| マイナスの数 | 計算式 | 答えの符合 |
| 1(奇数) | \(+×-\) | \(-\) |
| 2(偶数) | \(-×-\) | \(+\) |
| 3(奇数) | \(-×-×-\) | \(-\) |
| 4(偶数) | \(-×-×-×-\) | \(+\) |
| 5(奇数) | \(-×-×-×-×-\) | \(-\) |
前述の通り、マイナスは反対の性質があります。反対の反対は表です。そのためマイナスが偶数の場合、答えの符合はプラスです。それに対して、マイナスが奇数の場合は符合がマイナスになります。
整数だけでなく、小数や分数にマイナスがある場合であってもこの法則に従います。例えば、以下のようになります。
- \(-1×-1×-\displaystyle\frac{1}{2}=-\displaystyle\frac{1}{2}\)
マイナスの数が3個で奇数のため、答えはマイナスになります。掛け算と割り算の計算では、マイナスの数が偶数なのか奇数なのかによって、答えの符合が変化します。
累乗を用いた指数計算の方法
なお正の数と負の数では、掛け算や割り算と同じくらい重要な概念として累乗があります。同じ数をいくら掛けたのかを表す計算が累乗です。累乗では、例えば\(3×3\)を32と表します。また、\(4×4×4\)を43と表します。
読み方としては、32は3の2乗です。43は4の3乗です。
また、右上にある小さい数字を指数といいます。例えば43の場合、3が指数です。指数を確認することで、同じ数字をいくつ掛けるのか分かります。
累乗を用いた指数計算では、例えば以下のようになります。
- \(3^4=3×3×3×3=81\)
- \((-2)^3=-2×-2×-2=-8\)
- \(0.1^2=0.1×0.1=0.01\)
累乗の計算をするとき、指数をみることで、いくつの数を掛ければいいのか確認するようにしましょう。
累乗の計算は符合の違いとかっこに注意
なお、累乗の計算では符合の違いを認識することが、答えを出すときに最も重要です。例えば、以下の累乗の答えはどのようになるでしょうか。
- \(-3^2\)
- \((-3)^2\)
- \(-(-3)^2\)
この違いを理解しなければ、正しく累乗の計算をすることができません。そこで、指数のルールを学びましょう。指数には以下の性質があります。
- 直前の数字に対し、累乗をする:符合(-1)は含まない
符合を含めず、直前の数字だけを累乗するのが指数です。そのため、-32は以下のように計算します。
- \(-3^2=-1×3^2=-1×3×3=-9\)
-32には、-1が隠されています。そこで-1と32を分けて考えます。指数は直前の数字に対してのみ有効であり、符合(-1)を含めないルールになっているからです。

ただ先ほど、「\((-2)^3=-2×-2×-2=-8\)」と解説しました。指数は符合を含めないにも関わらず、なぜ(-2)3では-2を3つ掛けるのでしょうか。それは、かっこを使っているからです。
かっこには、「かっこ内にある式を一つの数字として考える」というルールがあります。(-2)3では、かっこの中に-2が存在します。そこで-2を一つの数字と考えると、(-2)3は「\((-2)^3=-2×-2×-2\)」となります。同じように考えると、(-3)2は以下のようになります。
- \((-3)^2=-3×-3=9\)
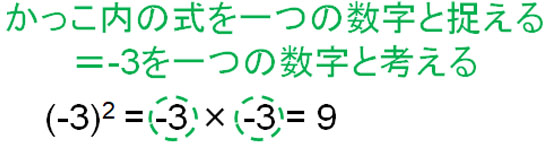
それに対して、-(-3)2はどのようになるのでしょうか。前述の通り、指数は直前の数字のみを累乗します。また、かっこの中にある式を一つの数として考えます。そのため、以下のような計算式になります。
- \(-(-3)^2=-1×(-3)^2=-1×-3×-3=9\)
(-3)の右にある指数は2です。そのため、-3を2つ掛けます。ただ、(-3)の前にある符合(-1)と分けて計算しなければいけません。その結果、上に記した計算式になります。
分数の累乗でもかっこに注意するべき
かっこがあるのかないのかによって、累乗を計算するときの答えが大きく異なります。分数の累乗でも、かっこに注意するようにしましょう。
例えば、以下の答えは何でしょうか。
- \(\displaystyle\frac{2^4}{3}\)
- \(\left(\displaystyle\frac{2}{3}\right)^4\)
指数は直前の数字のみ有効です。そのため、以下のように考えます。
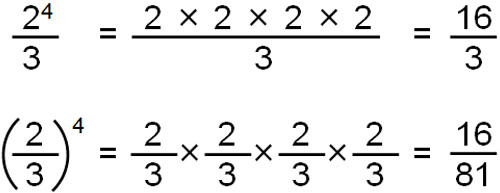
\(\displaystyle\frac{2^4}{3}\)では、2のみ4乗をします。直前の数字は2だからです。
一方で\(\left(\displaystyle\frac{2}{3}\right)^4\)では、\(\left(\displaystyle\frac{2}{3}\right)\)を4乗します。直前にかっこがあるため、かっこの中にある数字すべてに対して4乗します。
かっこがない場合、直前の数字だけ累乗しましょう。それに対して、かっこがある場合、かっこの中にある数字すべてを累乗しましょう。指数計算では、かっこがあるのかないのかによって、計算方法が変わることを理解しなければいけません。
練習問題:中学数学の掛け算・割り算・乗数
Q1. 次の計算をしましょう
- \(3×-4\)
- \(-30÷-5\)
- \(-4×-6×-3\)
A1. 解答
正の数と負の数を用いて掛け算または割り算をするとき、重要なのは「マイナスが偶数だと答えはプラスになり、マイナスが奇数だと答えはマイナスになる」ことです。そのため、答えは以下のようになります。
- \(3×-4=-12\)
- \(-30÷-5=6\)
- \(-4×-6×-3=-72\)
Q2. 次の計算をしましょう
- \(-3^2×(-2)^2\)
- \((-3)^3×8÷2^2\)
- \(-(-2)^4÷\displaystyle\frac{1}{3}×\left(-\displaystyle\frac{2}{3}\right)^2\)
A2. 解答
数学の問題を解くとき、最初に累乗を計算しなければいけません。累乗は一つの数字と意味は同じだからです。例えば\(12÷2^2\)という問題を解くとき、最初に22を計算しなければ問題を解くのは不可能です。22は\(2×2=4\)のため、\(12÷4=3\)となります。
同じように、最初に累乗の計算をしましょう。そうすると、以下のようになります。
- \(-3^2×(-2)^2=-9×4=-36\)
- \((-3)^3×8÷2^2=-27×8÷4=-54\)
(c)の問題は以下のように考えます。
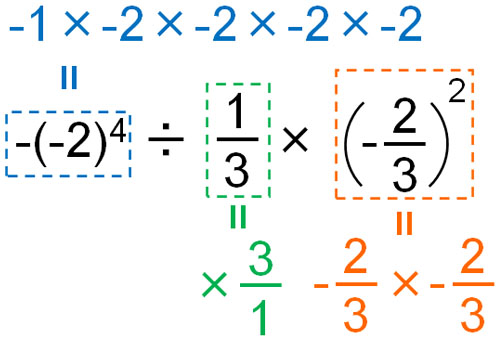
\(-(-2)^4÷\displaystyle\frac{1}{3}×\left(-\displaystyle\frac{2}{3}\right)^2\)
\(=-16×3×\displaystyle\frac{4}{9}\)
\(=-\displaystyle\frac{192}{9}\)
\(=-\displaystyle\frac{64}{3}\)
それぞれを分けて計算することで、最終的に掛け算だけの式にすることができます。
乗法と除法でプラスとマイナスの計算をする
プラスとマイナスの計算をどのようにするのか理解しなければ、まず数学での計算ができません。そこで掛け算(乗法)や割り算(除法)をするとき、符合がどのようになるのか学びましょう。
特にマイナスとマイナスの掛け算(または割り算)をするとき、なぜプラスになるのか理解できず、混乱する人が非常に多いです。そこで、なぜ負の数と負の数の掛け算で答えがプラスになるのか解説しました。
また重要なのは、マイナスが偶数だと答えがプラスになり、マイナスが奇数だと答えがマイナスになる事実です。
それに加えて、乗数の概念も学びましょう。乗数ではかっこが重要であり、どこにかっこがあるのかによって答えが違ってきます。これが、正の数と負の数で学ぶべき掛け算と割り算の考え方です。






