大きさがあり、外から力が加わっても変形しない物体を剛体といいます。剛体を棒につるす場合、棒は回転します。剛体によって生まれる回転する力を力のモーメントといいます。
力のモーメントを計算するとき、距離と重さが重要です。ただ角度を考慮する必要があるため、どのように角度を利用して力のモーメントを計算すればいいのか理解しましょう。
また力のモーメントを利用することにより、剛体のつり合いを計算できます。剛体が静止している状態というのは、力のモーメントが同じであることを意味しています。そこで、力のモーメントを利用して式を作れるようにしましょう。
それでは、どのように力のモーメントを計算すればいいのでしょうか。剛体に働く力のつり合いを解説していきます。
もくじ
剛体を回転させる力が力のモーメント
棒に剛体をつるすと回転させる力が働きます。力のモーメントでは棒と剛体の関係を考えます。例えば以下の図では、点Aに重りをつるすことにより、点Oを支点として棒には矢印の向きに回転する力が加わります。
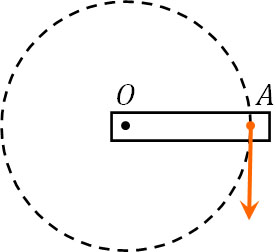
力のモーメントを計算するとき、支点からの距離と剛体による重力をかけます。長さ\(l\)の棒に対して、垂直に力\(F\)が加わる場合、力のモーメント\(M\)は以下の式によって表されます。
- \(M=l×F\)

ただこの式を覚える意味はなく、感覚的に理解できます。
力のモーメントを理解するとき、シーソーを想像しましょう。支点からの距離が同じ場合、重い側に力のモーメントは動きます。

なぜこのような現象が起こるかというと、力のモーメントでは力の大きさが重要だからです。また重さが違っていたとしても、以下のように距離を調節すれば力はつり合います。
加える力が弱くても、支点からの距離が遠い場合、力のモーメントは大きくなります。この現象は私たちが日常生活で感じているため、容易に理解できると思います。
ただ物理では、数式で表す必要があります。つまり、支点からの距離が遠くなるほど、また加える力が大きくなるほど、力のモーメントが大きくなるようにするのです。そこで、支点からの距離\(l\)と力の大きさ\(F\)をかけることで力のモーメント\(M\)を出しましょう。
角度によって変わる力のモーメントと垂直の関係
なお力のモーメントを計算するとき、支点から伸びる棒に対して、加える力の向きは必ず垂直でなければいけません。例えば以下の場合、線OAと加える力の向きは垂直です。

ただ、棒と力の向きが垂直の関係となっているとは限りません。例えば、以下のケースもあります。

このように垂直の関係になっていない場合、どのように考えればいいのでしょうか。
考え方は二つあります。一つ目は、力を分解する方法です。以下のように力を分解すると、棒に対して垂直方向の力を得るには、\(cosθ\)をかければいいとわかります。つまり、棒の長さ\(l\)と力の大きさ\(Fcosθ\)をかけることで、力のモーメント\(M\)を得ることができます。
- \(M=l×Fcosθ\)
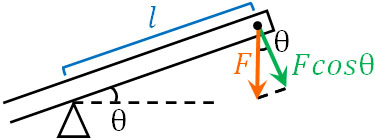
または、力の向きに対して垂直になるように、支点からの距離を測定しましょう。このとき、距離\(l\)に対して\(cosθ\)をかけることで力に対して垂直となる線を引くことができます。
なお力の延長線上を作用線と呼び、作用線上(直線上)であれば力の移動が可能です。そこで、支点からの距離\(lcosθ\)と力の大きさ\(F\)をかけましょう。
- \(M=lcosθ×F\)

どちらの方法で計算しても、\(M=lFcosθ\)によって力のモーメントを得ることができます。いずれにしても、棒と力の向きが垂直でない場合、角度を利用して計算すればいいことを理解しましょう。
力の作用線上であれば移動が可能
なお先ほど、作用線上(直線上)であれば、力を移動できることを解説しました。力の向きを変えてはいけません。ただ力の向きを変えないのであれば、自由に移動させることができるのです。
例えば棒ではなく、板に対して力を加える場面を考えてみましょう。以下のように支点Oを基準にした長方形の板に対して、以下のように点Bに力\(F\)を加えます。

この場合、力のモーメントはどのように計算すればいいのでしょうか。前述の通り、作用線上であれば自由に力を移動できます。そこでベクトルの向きを変えないように、以下のように移動させましょう。
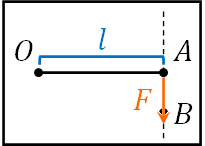
こうして、\(M=l×F\)によって力のモーメントを計算できます。
それでは、なぜ作用線上であれば力を移動させることができるのでしょうか。力のモーメントを計算するとき、必ず線と力の向きが垂直でなければいけません。そこで、OBの長さとOBに垂直な力を計算してみましょう。
角度を用いて計算すると、以下のようになります。
- OBの長さ:\(\displaystyle\frac{l}{cosθ}\)
- OBに垂直な力:\(Fcosθ\)
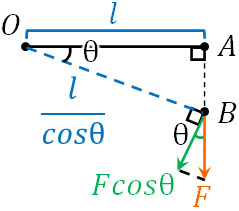
そこでOBの長さとOBに垂直な力をかけ、力のモーメントを計算すると以下のようになります。
\(M=\displaystyle\frac{l}{cosθ}×Fcosθ\)
\(M=l×F\)
こうして、作用線上で力を移動させたときと同じ式を得ることができました。このように計算上でも、作用線上(直線上)であれば力を動かしても問題ないことがわかりました。
力のモーメントの計算方法:正と負の考え方
それでは、実際に力のモーメントを計算してみましょう。力のモーメントには、時計回りの力(右回りの力)と反時計回りの力(左回りの力)があります。そこで、どちらか一つを正にしましょう。
どちらを正にしても問題ありません。計算結果は同じになるからです。例えば右回りの力を正にしたのであれば、左回りの力を負にしましょう。例えば以下の図について、点Oを支点とするとき、質量\(m\)、長さ\(l\)の棒での力のモーメントはどのようになるでしょうか。
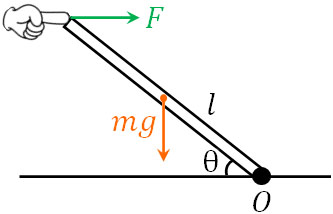
方法は2つあり、これまで説明した通り「力を分解する」または「力を作用線上で移動させる」ことによって力のモーメントを計算できます。
まず右回りと左回りのうち、どちらか一方を正にしましょう。どちらを正にしても問題ありません。仮に右回りの力を正にする場合、左回りの力は負になります。
・力を分解するケース
それでは、力を角度によって分解するパターンを確認しましょう。以下のように力を分解することによって、右向きの力と左向きの力をそれぞれ計算しましょう。
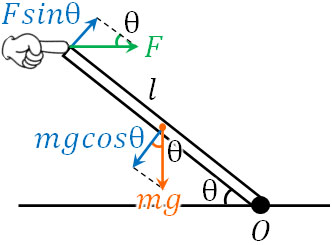
力のモーメントを計算するとき、このやり方のほうがわかりやすいです。力の分解をするとき、どこがθになるのかを把握すれば、このように力の分解が可能です。なお右向きの力を正とするため、以下のように力のモーメントに関する式を作ることができます。
\(M=Fsinθ·l-\displaystyle\frac{l}{2}·mgcosθ\)
質量\(m\)の棒では、上図より棒に垂直方向の力は\(mgcosθ\)です。ただ重力は物質の中心(棒の中点)に働くため、長さは\(\displaystyle\frac{l}{2}\)を利用します。
・力を作用線上で移動させるケース
次に力を作用線上で移動させる方法を解説していきます。力のモーメントを計算するとき、棒と力は必ず垂直でなければいけません。そこで、作用線上で以下のように力を移動させましょう。
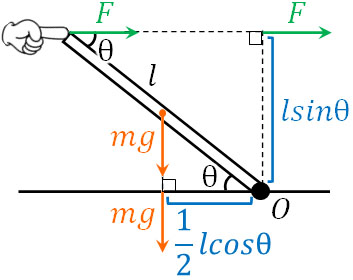
こうして、棒と力の向きが垂直になります。また右向きの力を正、左回りの力を負で力のモーメントの式を作ると以下のようになります。
\(M=Fsinθ·l-\displaystyle\frac{l}{2}·mgcosθ\)
力を分解するケースと計算結果は同じです。また、計算方法はどちらでも問題ありません。出題される問題に応じて、どちらの方法を利用して計算するのか決めましょう。
方程式を作り、剛体のつり合いを考える
次に、剛体が静止している状態(剛体のつり合い)を学びましょう。物体が動いておらず、静止している状態では、右回りの力と左回りの力が同じです。そこで、方程式を作れるようになりましょう。つまり右回りの力と左回りの力が同じようになるようにイコールで結ぶのです。
例えば、以下の図で棒が回転しておらず静止しているのであれば、作るべき式は次のようになります。
\(l·mg=x·Mg\)
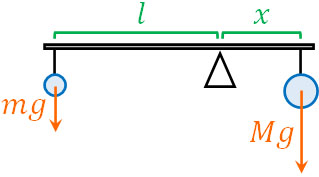
左回りの力と右向きの力を同じにするため、式は\(l·mg=x·Mg\)となります。
水平棒のつり合い:練習問題
それでは、ここまでの解説を参考にして力のモーメントに関する問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 以下の図のように、長さ\(l\)の棒ABが地面と平行になるようにACとBCが糸で壁とつながれています。また棒ABの中点に重さ\(m\)の重りをつるします。なおABとBCの角度をθ、重力加速度を\(g\)とします。また、棒と壁によって生じる摩擦力と棒の重さは無視できます。

- 点Aを支点とするとき、力のモーメントの式を作りましょう。また、力のつり合いの式を作りましょう。
- 点Bでの糸の張力\(T_B\)を求めましょう。
- 点Aでの糸の張力\(T_A\)を求めましょう。
- 点Aでの抗力\(N\)を求めましょう。
1) 点Aを支点とするとき、力のモーメントの式を作りましょう。また、力のつり合いの式を作りましょう
力のモーメントや力のつり合いの式を作るとき、一つの物体に着目しましょう。棒に着目する場合、3点で接しているため、重力を加えて4つの力が棒に働いているとわかります。
- 棒と壁:\(N\)
- 棒と糸AC:\(T_A\)
- 棒と糸BC:\(T_B\)
- 重力:\(mg\)
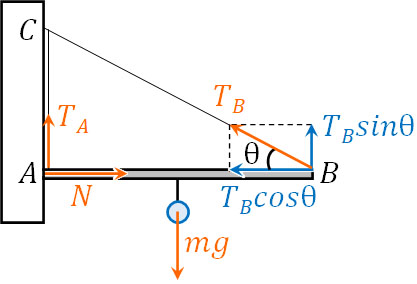
そこで点Aを支点として、右回りの力と左回りの力がつり合うように力のモーメントの式を作りましょう。以下のようになります。
\(\displaystyle\frac{l}{2}·mg=l·T_Bsinθ\) – ①
点Aが支点であるため、距離が0の\(T_A\)を式に含めないようにしましょう。またNは距離が0であるだけでなく、棒に対する角度が0であるため、力のモーメントには関与しません。
また、力のつり合いの式を作りましょう。静止しているというのは、力がつり合っていることを意味します。そこで水平方向と鉛直方向で以下のように式を作りましょう。
- 水平方向:\(N=T_Bcosθ\) – ②
- 鉛直方向:\(T_A+T_Bsinθ=mg\) – ③
こうして、力のつり合いの式を作ることができます。またこれらの式を作ることができれば、その後の計算は容易です。
2) 点Bでの糸の張力\(T_B\)を求めましょう
式①より、以下のようになります。
\(\displaystyle\frac{1}{2}l·mg=l·T_Bsinθ\)
\(T_B=\displaystyle\frac{mg}{2sinθ}\)
3) 点Aでの糸の張力\(T_A\)を求めましょう
式①と式③より、以下のようになります。
\(T_A+T_Bsinθ=mg\)
\(T_A=mg-T_Bsinθ\)
\(T_A=mg-\displaystyle\frac{mg}{2}\)
\(T_A=\displaystyle\frac{mg}{2}\)
4) 点Aでの抗力\(N\)を求めましょう
式①と式②より、以下のようになります。
\(N=T_Bcosθ\)
\(N=\displaystyle\frac{mg}{2sinθ}×cosθ\)
\(N=\displaystyle\frac{mg}{2tanθ}\)
力のモーメントを利用し、剛体のつり合いの式を作る
静止状態のつり合いを考えるとき、水平方向と鉛直方向の力のつり合いだけでなく、力のモーメントを考慮しましょう。棒や板に対して力が加わっている場合、剛体を回転させる力が働いています。
力のモーメントでは、静止しているのであれば右回りの力と左回りの力が同じです。正の力と負の力が同じであるため、物体は静止しているのです。そこで角度を用いて力を分解したり、力の作用線上で移動させたりして、力のモーメントの式を作りましょう。
なお力のモーメントを利用する問題が出題されるとき、力のつり合いも利用して問題を解かなければいけないケースが多いです。そこで一つの物体に着目し、物体に働いている力を書き出した後、力のモーメントと力のつり合いに関わる式を作りましょう。
力学では、回転するときにどう力が働くのか学びます。力のモーメントは回転するときに働く力を考える場合に重要です。そこで物体に働く力を探し、式を作れるようになりましょう。






