電磁誘導では、必ずコイルを学ぶことになります。そこで直流回路にコイルを含むとき、どのように電流が流れるのか学びましょう。
コイルに電流が流れるとき、自己誘導を起こします。電流が流れると同時に、自己誘導によって反対向きに電流が流れるため、スイッチを入れた直後はコイルに電流が流れません。つまり、コンデンサーとは反対の機能をもつ部品がコイルです。
また、コイルにはエネルギーを蓄積する働きがあります。そこで、コイルに蓄えられるエネルギーを計算できるようになりましょう。
それでは回路にコイルを含むとき、どのように公式を利用して計算すればいいのでしょうか。回路にコイルを含むときの考え方を解説していきます。
もくじ
スイッチを入れた直後、コイルに電流は流れない
導線に電流が流れると磁場が発生します。このとき、コイルは磁場の変化を嫌います。そのため電流の大きさが変わることによって磁場が変化する場合、コイルは磁場の変化を和らげるように電流を流します。
具体的には、コイルは自身を流れている電流の大きさが変化すると、コイルで電磁誘導が起こることで新たな電流を発生させます。これを自己誘導といいます。
自己誘導では、電流の変化とは反対向きの現象が起こります。電流を大きくする場合、自己誘導によって反対向きに電流が流れます。一方で電流を弱める場合、電流と同じ向きに新たな電流が生まれます。
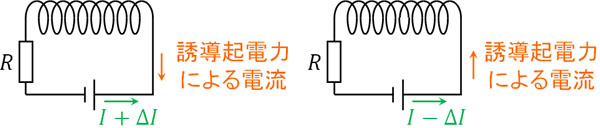
この性質により、コイルが回路に存在する場合、スイッチを入れた直後は回路に電流が流れません。自己誘導により、反対向きの電流が流れるため相殺されるからです。ただ時間が経過すると、徐々にコイルに電流が流れます。
コイルとコンデンサーの違いを比較する
そのためコイルが直流回路に存在する場合、以下のように考えましょう。
- スイッチを入れた直後:断線しているとみなす
- スイッチを入れ、十分な時間が経過した後:導線とみなす
自己誘導により、スイッチを入れた直後はコイルに電流が流れません。そのためスイッチを入れた直後では、コイルの部分は断線していると考えることができます。例えば以下の回路では、スイッチを入れた直後はコイルに電流が流れないので、コイルの部分を無視できます。

一方、時間経過と共にコイルに電流が流れるようになります。コイルは磁場の変化を嫌うものの、変化後の磁場環境に徐々に慣れていきます。そのため電流の大きさが変化しない場合、十分な時間が経過すれば、コイルによる電磁誘導が起こらなくなります。
つまり、コイルによる自己誘導によって発生していた逆向きの電流がなくなります。そのためスイッチを入れて十分な時間が経過している場合、コイルの抵抗はゼロなので、コイルを導線とみなすことができます。先ほどの回路であれば、以下のように変えることができます。
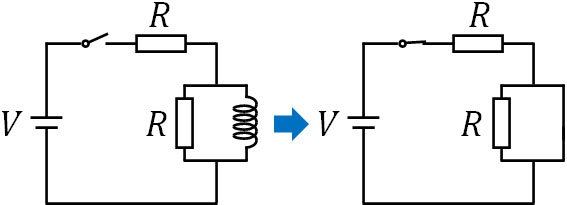
このように考えると、コイルとコンデンサーは逆の性質をもつとわかります。コンデンサーが直流回路にある場合、以下のように考えます。
- 電源につないだ直後:コンデンサーを導線とみなす
- 電源につなぎ、十分な時間が経過した:コンデンサーで断線される
コイルとコンデンサーの違いを理解すれば、コイルの性質を覚えやすくなります。
自己誘導がない場合とある場合のグラフの違い
それでは、コイルによる自己誘導がない場合とある場合では、どのような違いがあるのでしょうか。コイルがない場合、スイッチを入れた瞬間に電流\(I\)が流れます。たて軸を\(I\)、横軸を経過時間\(t\)とすると、オームの法則より電流の値は\(I=\displaystyle\frac{V}{R}\)となります。
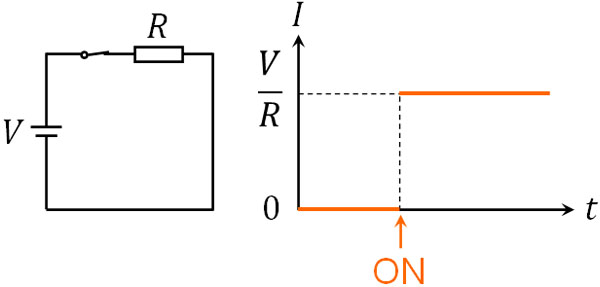
一方でコイルがある場合、前述の通り自己誘導が起こるため、スイッチを入れた直後は電流が流れません。また、時間経過と共に徐々に電流が流れます。そのため、以下のようなグラフになります。

十分な時間が経過すると、コイルを導線とみなすことができるため\(I=\displaystyle\frac{V}{R}\)となります。いずれにしても、コイルが存在する直流回路ではこのようなグラフになることを理解しましょう。
スイッチを切った後の電流の様子と自己誘導
それでは、スイッチを切った後はどのように考えればいいのでしょうか。直流回路にコイルがない場合、スイッチを切った瞬間に電流が流れなくなります。
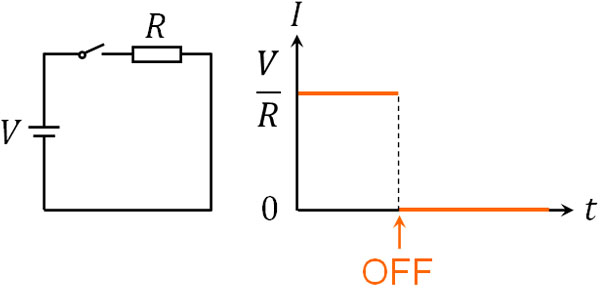
一方でコイルが回路にある場合、スイッチを切ったとしても少しの間は電流が流れます。スイッチを切ると、コイル周辺の電場が弱くなります。コイルは電場の変化を嫌うため、電場を増やすように自己誘導によって電流を増やすのです。
言い換えると、スイッチを切ることによって、なくなった電流を補うように電磁誘導を起こすのです。そのため、以下のようなグラフになります。
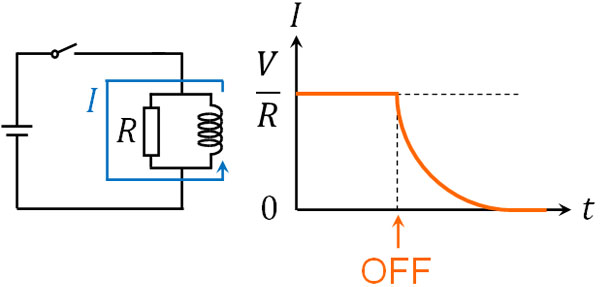
このように、スイッチを切った後であってもわずかな時間、電流を流す性質をもつのがコイルです。
コイルに蓄えられるエネルギーの公式
スイッチを切った後も電流が流れるというのは、コイルにはエネルギーが蓄えられていることを意味しています。エネルギーが存在するため、スイッチを切った後であってもエネルギーを放出することができるのです。
このとき、自己インダクタンス\(L\)のコイルに電流\(I\)が流れている場合、コイルに蓄えられているエネルギー\(U\)は以下の公式によって表すことができます。
- \(U=\displaystyle\frac{1}{2}LI^2\)
この公式については、公式の作り方を覚えるのではなく、暗記しても問題ありません。公式を覚えるほうが素早く計算できます。
面積の計算によってエネルギーの公式を得る
ただ公式を覚えるというのは、「公式の導出方法を理解しなくてもいい」という意味ではありません。物理では、必ず公式の導き出し方を学びましょう。そうでないと物理を学ぶ意味がなく、どのように公式を得るのか理解する必要があります。
それでは自己インダクタンスが\(L\)であるコイルを利用し、電流\(I\)が流れており、\(Δt\)秒での電流の変化が\(ΔI\)としましょう。公式は\(V=L\left|\displaystyle\frac{ΔI}{Δt}\right|\)なので、コイルの両端で生じる誘電起電力\(V\)の大きさは以下になります。
- \(V=L\displaystyle\frac{ΔI}{Δt}\)
なお、1秒あたりの電気量\(Q\)が電流の定義です。そのため、電流は\(I=\displaystyle\frac{Q}{t}\)と表すことができます。式を変形すると、\(Q=It\)です。そのため電流\(I\)が\(Δt\)秒、流れるときの電気量は以下になります。
- \(Q=IΔt\)
電気による仕事というのは、電気量\(Q\)を電圧\(V\)の高さまで持ち上げるために必要なエネルギーであるため、\(W=QV\)が公式です。そのため、非常に短い時間\(Δt\)について、電気による仕事\(ΔW\)は以下のように計算できます。
\(ΔW=IΔt×L\displaystyle\frac{ΔI}{Δt}\)
\(ΔW=LIΔI\)
それでは、非常に短い時間(\(Δt\)の時間)が経過し、そのつど\(ΔI\)の電流が上昇していく場合、どのようなグラフになるでしょうか。横軸を\(I\)、たて軸を\(LI\)とすると、微小時間\(Δt\)で電流が\(ΔI\)変化するときの仕事\(ΔW\)はグラフの以下の部分が該当します。
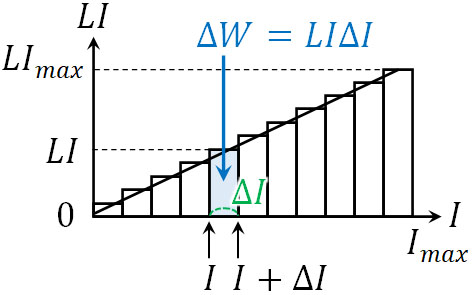
なお最初は電流が流れていないため、\(I=0\)からスタートすることになります。また、十分な時間が経過すると、電流は最高値\(I_{max}\)に到達します。そこで、電流\(I\)が\(I_{max}\)まで変化するとき、すべての\(ΔW\)を足しましょう。
これを計算するためには積分が必要になります。ただ幸いなことに、\(Δt\)が非常に短い場合、実質的に三角形の面積の計算と同じになります。数学で積分を学ぶとき、「微小変化(\(Δt\)の変化)を近似する」と教わったと思うので、これについては問題なく理解できると思います。
そこで、三角形の面積を計算すると以下の式を得ることができます。
- \(W=\displaystyle\frac{1}{2}LI_{max}^2\)
なお仕事\(W\)が行われたのであれば、コイルには同じ値の内部エネルギー\(U\)が蓄積します。つまり、以下のように表すことができます。
- \(U=\displaystyle\frac{1}{2}LI_{max}^2\)
回路に電流が流れていない状態で電流\(I\)を流す場合、\(I_{max}=I\)です。こうして、先ほどの公式である\(U=\displaystyle\frac{1}{2}LI^2\)を得ることができました。
コンデンサーとコイルでは、エネルギーを得る公式が似ている
電磁気学でコイルを学ぶのであれば、既にコンデンサーの性質を理解していると思います。コンデンサーとコイルを比較すると、エネルギーを得る公式が似ています。コンデンサーに蓄積する静電エネルギーは以下の公式を利用して計算します。
- \(U=\displaystyle\frac{1}{2}CV^2\)
コンデンサーでは、どれだけ電荷を蓄えられるのかが重要です。そのため、静電エネルギーの計算では電圧\(V\)を利用します。
一方でコイルの場合、電磁誘導では電流の大きさが重要になります。電流が流れることによって磁場が変化するためです。そこで電圧ではなく、電流を利用することによってコイルに蓄積するエネルギー\(U\)を計算しましょう。
コイルに蓄積するエネルギーの練習問題
それでは、コイルに蓄積するエネルギーに関する練習問題を解きましょう。以下の問題の答えは何でしょうか。
- \(Δt\)秒でコイルを流れる電流が\(I\)から\(6I\)へと変化し、コイルに誘導起電力\(V\)を生じました。コイルが蓄えているエネルギーの変化量はいくらですか。
コイルを流れる電流が変化するとき、コイルに生じる誘電起電力を得る公式は\(V=L\left|\displaystyle\frac{ΔI}{Δt}\right|\)です。そこで、以下のように計算して自己インダクタンスを得ましょう。
\(V=L\left|\displaystyle\frac{ΔI}{Δt}\right|\)
\(L=\displaystyle\frac{VΔt}{5I}\)
またエネルギー変化量\(ΔU\)の計算では、変化後から変化前を引けばいいです。そのため、以下の計算になります。
\(ΔU=\displaystyle\frac{1}{2}·\displaystyle\frac{VΔt}{5I}(6I)^2-\displaystyle\frac{1}{2}·\displaystyle\frac{VΔt}{5I}I^2\)
\(ΔU=\displaystyle\frac{36VIΔt}{10}-\displaystyle\frac{VIΔt}{10}\)
\(ΔU=\displaystyle\frac{7VIΔt}{2}\)
こうして、エネルギーの変化量は\(ΔU=\displaystyle\frac{7VIΔt}{2}\)と計算できました。
コイルを含む回路とエネルギーの公式を学ぶ
電流の大きさが変化することにより、自己誘導によって電流を発生する装置がコイルです。直流回路にコイルが存在する場合、スイッチを入れた直後は電流が流れません。ただ、時間経過と共に徐々に電流が流れます。
そこで回路にコイルが存在する場合、スイッチを入れた直後は断線しているとみなしましょう。一方、十分な時間が経過した後はコイルを導線とみなしましょう。こうして、回路に関わる計算ができるようになります。
また回路に電流が流れることにより、コイルにエネルギーが蓄えられます。事実、スイッチを切るとコイルから電流が流れます。磁場が変化することで電磁誘導が起こり、コイルに誘導起電力を生じるのです。そこで、コイルがもつエネルギーを計算できるようになりましょう。
コイルを学ぶとき、コンデンサーの内容も復習しましょう。コンデンサーに比べて、コイルは性質が反対となっていることがあれば、似ていることもあります。コイルとコンデンサーを比較することにより、回路でのコイルの性質を覚えやすくなります。






