コンデンサーに電荷が蓄積している場合、電荷による影響によって静電気力(クーロン力)が発生します。2つの金属板が荷電しているとき、互いに引き合う(または反発する)のは既に理解していると思います。
それでは、2つの金属板を引き離す場合、どのような変化があるのでしょうか。また、極板が引き合うときの力(極板間引力)はいくらでしょうか。
極板間引力では、静電気力(クーロン力)に加えて、仕事、静電エネルギーを利用して引き合う力を計算します。
仕事とエネルギーは意味がほぼ同じです。そこで、どのように仕事とエネルギーを利用して引き合う力を計算すればいいのか解説していきます。
もくじ
静電気力により、コンデンサーの極板は引き合っている
正電荷同士(または負電荷同士)は反発します。一方で正電荷と負電荷は引き合います。このような力を静電気力(クーロン力)といいます。
充電によってコンデンサーに電荷が存在する場合、必ず正電荷と負電荷の金属板が向かい合うことになります。つまり、極板間では静電気力によって引き合う力が発生しています。

極板は固定されているため、動くことはありません。ただ静電気力により、常に引き合う力が働いているのです。この力を極板間引力といいます。
力\(F\)は一定であり、静電気力と外力はつり合っている
それでは、極板間引力を計算するにはどうすればいいのでしょうか。方法としては、極板を少しだけ動かすときの仕事を計算します。
前述の通り、極板は固定されているため、実際には極板は動きません。そこで、少しだけ極板を動かすと仮定するのです(実際には、極板が動くことはない)。極板間の距離が\(d\)のとき、\(Δd\)だけ引き離すことで極板間の距離を大きくしましょう。つまり、極板間の距離は\(d\)から\(d+Δd\)へと変化します。
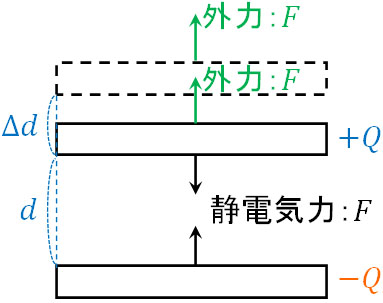
ゆっくり動かす場合は加速度がなく、外力\(F\)と静電気力\(F\)はつり合っており、\(F\)の値は同じです。また常に同じ力\(F\)で外力を加え、極板を移動させることになるため、\(W=Fx\)を利用することで外力による仕事を計算できます。
動かす距離は\(Δd\)であるため、外力による仕事は\(W=FΔd\)となります。こうして、極板を引き離すときに必要な力を計算することができました。
コンデンサーの電気容量\(C\)の変化
それでは、極板を引き離すことによってコンデンサーの電気容量\(C\)はどのように変化するのでしょうか。コンデンサーの公式より、極板の面積を\(S\)、真空中の誘電率を\(ε_0\)とすると、以下のように電気容量\(C\)を計算できます。
- \(C=ε_0\displaystyle\frac{S}{d}\)
また極板を動かすことで極板間の距離が\(d+Δd\)になる場合、電気容量\(C’\)は以下のようになります。
- \(C’=ε_0\displaystyle\frac{S}{d+Δd}\)
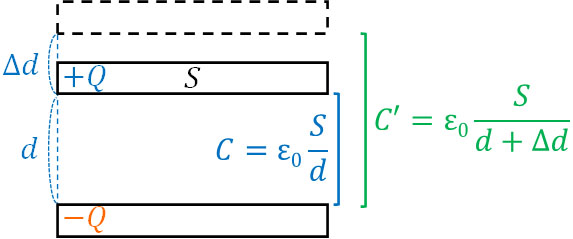
こうして、操作を行う前後の電気容量を計算することができました。
公式を用いた静電エネルギーの計算方法
なぜ電気容量の計算をしたかというと、電気容量を得ることができれば静電エネルギーの計算が可能だからです。コンデンサーがもつ静電エネルギー\(U\)は以下の公式によって計算できます。
- \(U=\displaystyle\frac{Q^2}{2C}\)
電気量保存の法則より、極板を引き離しても電気量\(Q\)に変化はありません。極板は独立しており、電荷は動けないからです。また電気量は勝手に生まれたり、消えたりしません。一方、先ほど計算した通り電気容量は変化します。つまり、コンデンサーが保有する静電エネルギーが変化します。
そこで、極板を動かす前と後でコンデンサーがもつ静電エネルギーを計算しましょう。極板を動かす前の静電エネルギー\(U\)の計算では、公式に\(C=ε_0\displaystyle\frac{S}{d}\)を代入しましょう。また、極板を動かした後の静電エネルギー\(U’\)の計算では、公式に\(C’=ε_0\displaystyle\frac{S}{d+Δd}\)を代入しましょう。
- \(U=\displaystyle\frac{dQ^2}{2ε_0S}\)
- \(U’=\displaystyle\frac{(d+Δd)Q^2}{2ε_0S}\)
こうして、極板を動かす前と動かした後の静電エネルギーを計算することができました。
仕事と静電エネルギーの関係から力\(F\)を求める
ここまでの計算を利用して、静電気力\(F\)を計算しましょう。仕事とエネルギーは意味が同じであり、仕事をすることによってエネルギーが増えたり減ったりします。また、操作の前後でエネルギーの合計は変わりません。
力学ではエネルギー保存則を利用します。電磁気学でも、エネルギー保存則を利用して式を作りましょう。
静電エネルギー\(U\)をもつコンデンサーに対して、外力を加えることで仕事\(W\)をすることにより、結果としてコンデンサーの静電エネルギーは\(U’\)へと変化します。そのため、以下の関係となります。
- 操作前の静電エネルギー\(U\)+ 外力による仕事\(W\) = 操作後の静電エネルギー \(U’\)
エネルギーと仕事の関係を利用して式を作りましょう。以下のように計算します。
\(U+W=U’\)
\(\displaystyle\frac{dQ^2}{2ε_0S}+FΔd=\displaystyle\frac{(d+Δd)Q^2}{2ε_0S}\)
\(FΔd=\displaystyle\frac{(d+Δd)Q^2}{2ε_0S}-\displaystyle\frac{dQ^2}{2ε_0S}\)
\(FΔd=\displaystyle\frac{ΔdQ^2}{2ε_0S}\)
\(F=\displaystyle\frac{Q^2}{2ε_0S}\)
こうして、静電気力(外力)が\(F=\displaystyle\frac{Q^2}{2ε_0S}\)になると計算できました。また静電気力は極板間引力を意味します。極板間引力を得るとき、仕事とエネルギーを利用して計算しましょう。
なお電気量\(Q\)、真空中の誘電率\(ε_0\)、極板の面積\(S\)は一定であるため、極板間引力\(F\)の値に変化はなく、定数であるとわかります。
極板を動かしても電気量は同じであるため、電場も一定です。一様の電場では静電気力が一定であるため、極板間引力\(F\)が定数になるのは当然の結果です。
仕事とエネルギーを利用して極板間引力を得る
極板間引力を計算するとき、仕事とエネルギーの関係を利用しましょう。解き方を理解していないと難しいものの、解き方を知っていれば極板間引力を得ることができます。
コンデンサーに存在する極板は固定されているため、実際には動きません。ただ、\(Δd\)の距離を動かすと仮定して式を作りましょう。極板を引き離す場合、電気量\(Q\)は変化しないものの、電気容量\(C\)が変化します。結果として、静電エネルギー\(U\)も変化します。
そこで力学的エネルギー保存則を利用して、外力による仕事とエネルギーを用いた式を作りましょう。これにより、静電気力(=極板間引力)を計算できます。
複数の公式を利用することにより、極板間引力を計算できます。力のつり合いや仕事とエネルギーの関係を利用して、極板間引力を計算できるようになりましょう。






