ジュールの法則：電力やジュール熱、公式、内部エネルギーの関係

電流を利用することにより、熱を発生させることができます。ドライヤーやオーブンなど、あなたが日常的に利用している電化製品には、電気を利用することによって発熱させている製品が多いです。

電気と熱の関係で重要な法則がジュールの法則です。電気によって発生する熱をジュール熱と呼び、ジュール熱は電力と時間に比例します。

ジュールの法則を学ぶとき、公式がもつ意味を理解しましょう。ジュール熱を得る公式は内部エネルギーや仕事、オームの法則を利用することによって計算できます。公式を覚える必要はなく、いつでも作れるようになりましょう。

それでは、電力とジュール熱にはどのような関係があるのでしょうか。また、どのように公式を利用すればいいのでしょうか。ジュールの法則を利用し、熱を計算する方法を解説していきます。

1 抵抗によって熱が発生する
- 1.1 ジュール熱が発生する理由
2 内部エネルギーと仕事の関係を利用する
- 2.1 ジュール熱を計算する公式を得る
- 2.2 オームの法則を利用し、ジュールの法則で利用される公式を得る
3 ジュール熱は電力量でもある：電力と電力量の関係
- 3.1 電流による仕事率が電力
- 3.2 自由電子の運動とジュール熱、電力量に関する練習問題
4 ジュールの法則の原理を学ぶ

抵抗によって熱が発生する

電気では電圧、電流、抵抗の3つが重要な要素になります。このとき、抵抗に電流が通ると熱が発生します。また、発生する熱をジュール熱といいます。抵抗に電流が流れるとき、抵抗で消費される熱エネルギーがジュール熱です。

熱を発生させる電化製品というのは、製品の中に非常に大きい抵抗が存在します。電気エネルギーを熱エネルギーへと変換することにより、ジュール熱を得るのです。

例えば以下のドライヤーでは、製品の中に電熱線（抵抗）があります。電熱線に風が当たることによって温風を得ることができ、髪を効率的に乾かすことができます。

そこで、なぜ抵抗に電流が流れることによってジュール熱が発生するのか学びましょう。

ジュール熱が発生する理由

電流が発生しているというのは、自由電子が動いていることを意味しています。抵抗が大きく、ジュール熱が発生しているとき、自由電子が陽子に衝突しています。

自由電子が動いているとき、当然ながら自由電子は運動エネルギーをもっています。ただ衝突により、自由電子がもつ運動エネルギーは陽子へ移動します。

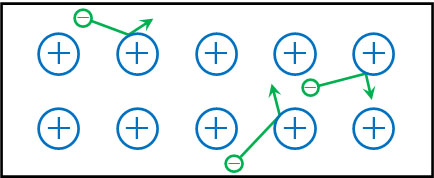
陽子は電子に比べて非常に重く、動くことができません。金属中の陽子は動けないものの、振動することができます。言い換えると、陽子は熱運動をすることによってジュール熱を放出します。

熱力学では、運動エネルギーが大きいと温度が高くなることを学びます。運動エネルギーが大きいと、それに比例して内部エネルギー（温度）が上昇するのです。熱力学で学ぶ気体の分子運動を復習すると、理想気体の単原子分子では以下の式が成り立ちます。

\(\displaystyle\frac{1}{2}m\overline{v^2}=\displaystyle\frac{3}{2}kT\)

このように運動エネルギーが大きいと、その分だけ温度\(T\)が高くなります。また分子の運動量は気体の圧力\(P\)や体積\(V\)の影響を受けず、温度\(T\)のみが決定要因となります。これが、陽子の運動エネルギー（熱振動）が大きいとジュール熱が大きくなる理由です。

内部エネルギーと仕事の関係を利用する

それでは、どのようにしてジュール熱を計算すればいいのでしょうか。一様な電場での位置エネルギー\(U\)を学ぶとき、以下の公式を知ることになります。

\(U=qV\)

電荷\(q\)の物体が電位差\(V\)の高さにあるとき、位置エネルギー\(U\)はこの公式を利用して計算できます。力学では、内部エネルギーを得る公式は\(mgh\)です。一方、電気では\(qV\)が内部エネルギーを得る公式です。

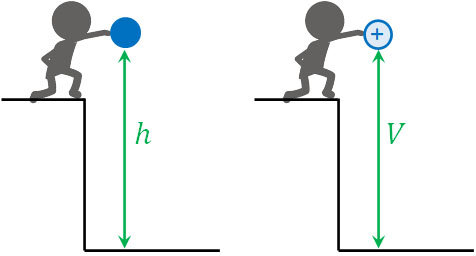
また物体がもつ位置エネルギー\(U\)は物体に対して行われた仕事\(W\)と同じであり、\(U=W\)です。これは電荷をもつ物体でも同様であるため、以下のようになります。

\(W=qV\)

仕事\(W\)の単位はジュール（J）です。なお力学では、仕事を得る公式として\(W=Fx\)を学びます。つまり、力の大きさ（ニュートン）と移動距離（メートル）をかけることで仕事を得られます。つまり、ジュール（J）の単位はN·mでもあります。

同様に、電荷\(q\)の物体を電位差（高さ）\(V\)の場所まで運ぶとき、ジュール熱の大きさ（J）を得るためには、\(W=qV\)[J]を利用して計算すればいいとわかります。

ジュール熱を計算する公式を得る

\(W=qV\)によってジュール熱を計算できることを復習すれば、ジュール熱を計算するために必要な公式を得ることができます。具体的には、\(W=qV\)を利用して電流\(I\)を利用する公式へ変換しましょう。

電流の定義より、1秒間に流れる電気量\(q\)を表しているのが電流\(I\)です。そのため、\(t\)秒間で電気量\(q\)が流れるとき、以下の式によって電流を得ることができます。

\(I=\displaystyle\frac{q}{t}\)

この公式を変形すると、\(q=It\)[C]となります。そこで、\(q=It\)を\(W=qV\)に代入しましょう。

\(W=IVt\)

電場が電荷をもつ物質を運ぶときにした仕事\(W\)[J]を計算するとき、\(W=IVt\)によって得られるとわかりました。

なお、衝突によってすべてのエネルギーが陽子に移り、陽子の運動エネルギー（熱振動）として利用される場合、陽子から発せられるジュール熱\(Q\)[J]は\(W=Q\)となります。つまり、電荷をもつ物体（自由電子）の位置エネルギーが陽子の運動エネルギーへ変換され、陽子が振動することでジュール熱が発生するのです。

なお、仕事\(W\)もジュール熱\(Q\)も単位はジュールであり、\(W=Q\)となるのは問題なく理解できると思います。そこで、\(W=IVt\)を以下のように変えましょう。

\(Q=IVt\)

こうして、電荷をもつ物体（自由電子）の位置エネルギーが減少した分だけ、陽子が振動することでジュール熱が発生するとわかります。

ジュールの法則を学ぶとき、教科書には公式が掲載されているものの、公式の導出方法や考え方が記載されていないことがあります。また、教え方が下手な教師はここまで解説したことを説明せず、公式を暗記するように教えるかもしれません。

ただ、それでは物理を学ぶ意味がありません。ジュール熱を得る公式を導き出すとき、公式の変形は難しくありません。また、ほかの分野の復習にもなります。そこで公式を覚えず、公式を作れるようになりましょう。

オームの法則を利用し、ジュールの法則で利用される公式を得る

\(Q=IVt\)であるとわかれば、ジュールの法則で利用される公式を得ることができます。オームの法則を利用して、\(Q=IVt\)へ代入しましょう。

オームの法則より、\(V=RI\)です。そこで\(Q=IVt\)へ代入すると、以下のようになります。

\(Q=I^2Rt\)

またオームの法則より、\(V=RI\)であるため、\(I=\displaystyle\frac{V}{R}\)です。そこで\(I=\displaystyle\frac{V}{R}\)を\(Q=IVt\)へ代入すると、以下のようになります。

\(Q=\displaystyle\frac{V^2t}{R}\)

こうして、以下の関係が成り立つとわかります。

\(Q=IVt=I^2Rt=\displaystyle\frac{V^2t}{R}\)

この関係をジュールの法則といいます。

ジュール熱は電力量でもある：電力と電力量の関係

なお、ジュール熱\(Q\)[J]は電力量でもあります。電流が行う仕事を電力量と呼び、記号は\(W\)[J]を利用します。ジュール熱\(Q\)[J]と電力量\(W\)[J]は同じであるため、公式は以下になります。

\(W=IVt=I^2Rt=\displaystyle\frac{V^2t}{R}\)

\(Q\)を\(W\)に変えることにより、電力量の計算が可能です。それでは、なぜジュール熱と電力量が同じになるのでしょうか。

例えば物を落下させると、内部エネルギーは運動エネルギーへと変換されます。つまり、スピードが上昇します。また仕事をすると、その分だけ内部エネルギー（または運動エネルギー）が上昇します。

同じように、電流によって仕事が行われると、その分だけ熱運動で利用されるエネルギーが上昇します。そのため、ジュール熱\(Q\)[J]と電力量\(W\)[J]は同じ式となるのです。

電流による仕事率が電力

電力量\(W\)というのは、電力が\(t\)秒で行った仕事を指します。それでは、1秒間で電力が行う仕事率はどのように計算すればいいのでしょうか。

電流が1秒間で行う仕事（仕事率）を電力といいます。\(t\)[s]での電力量が\(W\)[J]であるため、電力\(P\)[J/s]を計算するためには、電力量\(W\)を時間\(t\)で割ればいいとわかります。つまり、電力\(P\)を得る公式は以下になります。

\(P=\displaystyle\frac{W}{t}\)

また前述の通り、ジュールの法則と電力量の関係より、以下の公式が成り立ちます。

\(W=IVt=I^2Rt=\displaystyle\frac{V^2t}{R}\)

そこで、この式を\(P=\displaystyle\frac{W}{t}\)へ代入しましょう。

\(P=IV=I^2R=\displaystyle\frac{V^2}{R}\)

こうして、電力\(P\)の計算に必要な公式を得ることができました。電力量\(W\)の公式から時間\(t\)を取り去ることによって、電力\(P\)の公式を導出できます。

なお電力\(P\)の単位はW（ワット）です。電力\(P\)の単位はJ/sでもあり、W（ワット）でもあるのです。電化製品でW（ワット）が記されていることは多く、多くの人にとって電力は馴染みがあると思います。

物理では、電力量の記号として\(W\)[J]を利用する一方、電力\(P\)の単位でW（ワット）を利用します。電力量の記号である\(W\)と電力\(P\)の単位であるW（ワット）を間違えないようにしましょう。

自由電子の運動とジュール熱、電力量に関する練習問題

それでは、次に自由電子の運動とジュール熱、電力量の関係を学びましょう。練習問題を利用することにより、自由電子の運動がどのように熱へ変換されるのか理解するのです。以下の問題を解いてみましょう。

断面積\(S\)、長さ\(l\)の金属棒に電圧\(V\)を加えると電流が流れました。自由電子に着目すると、電子は電場\(E\)の影響を受けて加速し、\(t\)秒後に速さ\(v\)となります。ただ\(t\)秒後に熱振動するイオンと衝突し、速さは0になり、これを繰り返します。

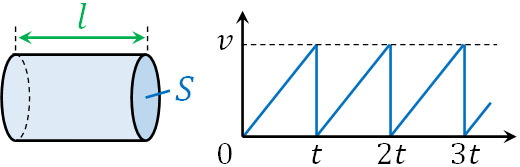
この場合、平均するとこの電子は一定の速さ\(\overline{v}\)で動いているとみなすことができます。なお、金属棒には単位体積あたり\(n\)個の自由電子が存在し、すべての電子は同じ運動をしています。

電子の電荷が\(-e\)のとき、電子が電場から受ける力の大きさ\(F\)はいくらですか。
電子が金属中のイオンと衝突する直前の速さ\(v\)を求めましょう。なお、電子の質量を\(m\)とします。
電子の速さ\(v\)を利用して、金属内を流れる電流\(I\)を計算しましょう。
金属の抵抗\(R\)が\(R=\displaystyle\frac{2ml}{ne^2tS}\)であることを示しましょう。
電子がイオンと衝突することで失う運動エネルギーを利用して、金属内に存在するすべての電子が1秒間に消費する運動エネルギー\(P\)を求めましょう。なお、答えには抵抗\(R\)を含めましょう。

電力やジュール熱に関する問題であるものの、問のほとんどはこれまで学んできたことの復習になります。そこで、復習を含めて問題を解きましょう。

1) 電子の電荷が\(-e\)のとき、電子が電場から受ける力の大きさ\(F\)はいくらですか

一様な電場では、電子が電場から受ける力は\(F=qE\)です。また、電圧\(V\)は電場\(E\)と距離\(d\)をかけることによって得られるため、\(V=Ed\)です。そのため、\(E=\displaystyle\frac{V}{d}\)となります。

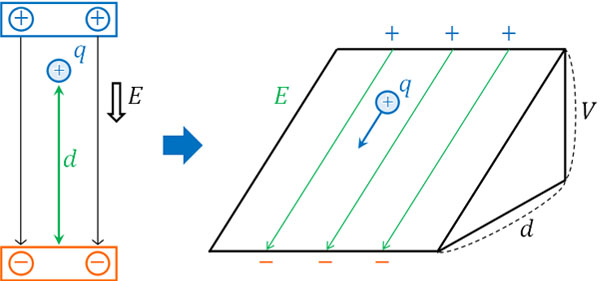
なお問題文より、金属棒の長さは\(l\)なので、\(E=\displaystyle\frac{V}{l}\)です。そこで、\(E=\displaystyle\frac{V}{l}\)を\(F=qE\)に代入しましょう。なお、電子の電荷は\(-e\)なので、\(q=e\)です。

\(F=qE\)

\(F=\displaystyle\frac{eV}{l}\)

こうして、力の大きさは\(F=\displaystyle\frac{eV}{l}\)となります。

2) 電子が金属中のイオンと衝突する直前の速さ\(v\)を求めましょう。なお、電子の質量を\(m\)とします

電子は電場による力を受けて加速しています。そこで、以下の運動方程式を作りましょう。

\(F=ma\)

\(\displaystyle\frac{eV}{l}=ma\)

\(a=\displaystyle\frac{eV}{lm}\)

電子の加速度は\(a=\displaystyle\frac{eV}{lm}\)です。また\(t\)秒後の速さ\(v\)を計算するため、等加速度直線運動の公式を利用しましょう。

\(v=at\)

\(v=\displaystyle\frac{eVt}{lm}\)

こうして、電子がイオンと衝突する直前の速さは\(v=\displaystyle\frac{eVt}{lm}\)と計算できました。

3) 電子の速さ\(v\)を利用して、金属内を流れる電流\(I\)を計算しましょう

電子に着目すると、\(v\)[m/s]で\(t\)秒が経過する場合、動いた距離は\(vt\)[m]です。また断面積は\(S\)[m²]であるため、\(t\)[s]で電子が動く金属の体積は\(vtS\)[m³]です。

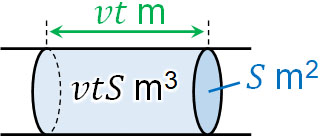
なお、金属棒には単位体積あたり\(n\)個の自由電子が存在するため、\(vtS\)[m³]に存在する電子の数は\(nvtS\)[個]です。また電子の電荷は\(-e\)であるため、全体の電気量は\(envtS\)[C]です。

前述の通り、電流は\(I=\displaystyle\frac{q}{t}\)によって計算できます。全体の電気量は\(envtS\)であるため、式に代入しましょう。

\(I=\displaystyle\frac{q}{t}\)

\(I=envS\)

こうして、電流は\(I=envS\)とわかります。

4) 金属の抵抗\(R\)が\(R=\displaystyle\frac{2ml}{ne^2tS}\)であることを示しましょう。

オームの法則より、\(V=RI\)であるため、\(R=\displaystyle\frac{V}{I}\)です。そこで、\(V\)または\(I\)へ値を代入することによって答えを得ましょう。

なお、抵抗を計算するためには、電子の平均の速さ\(\overline{v}\)を得なければいけません。図より、平均の速さは\(\overline{v}=\displaystyle\frac{v}{2}\)とわかります。

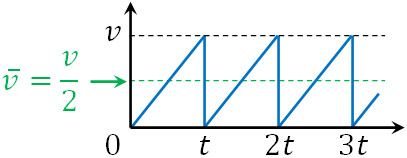
電子の平均スピードは最高スピードの2分の1となるため、電流の平均値は\(I=\displaystyle\frac{envS}{2}\)です。

また先ほど、\(v=\displaystyle\frac{eVt}{lm}\)と計算しました。そこで、この式を代入しましょう。

\(I=\displaystyle\frac{envS}{2}\)

\(I=\displaystyle\frac{enS}{2}×\displaystyle\frac{eVt}{lm}\)

\(V=\displaystyle\frac{2mI}{ne^2tS}\)

そこで、\(R=\displaystyle\frac{V}{I}\)へ\(V=\displaystyle\frac{2mI}{ne^2tS}\)を代入しましょう。

\(R=\displaystyle\frac{V}{I}\)

\(R=\displaystyle\frac{1}{I}×\displaystyle\frac{2mI}{ne^2tS}\)

\(R=\displaystyle\frac{2ml}{ne^2tS}\)

こうして、\(R=\displaystyle\frac{2ml}{ne^2tS}\)とわかりました。

5) 電子がイオンと衝突することで失う運動エネルギーを利用して、金属内に存在するすべての電子が1秒間に消費する運動エネルギー\(P\)を求めましょう。なお、答えには抵抗\(R\)を含めましょう

1つの電子がもつ運動エネルギーは\(t\)秒間で\(\displaystyle\frac{1}{2}mv^2\)になります。これをつまり、1つの電子がイオンと衝突することで、\(t\)秒後に\(\displaystyle\frac{1}{2}mv^2\)の運動エネルギーを失うことを意味しています。

また、金属棒の体積は\(Sl\)であり、単位体積あたり\(n\)個の自由電子が存在するため、金属棒に存在する電子の総数は\(nSl\)です。

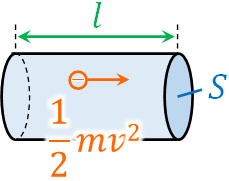
そのため、金属棒に存在する電子全体では、\(t\)秒間で以下の運動エネルギーが失われます。

\(\displaystyle\frac{1}{2}mv^2×nSl\)

それでは、\(t\)秒ではなく1秒間で失われるエネルギー\(P\)はいくらでしょうか。比例式を利用して計算しましょう。

\(t:1=\displaystyle\frac{1}{2}mv^2×nSl:P\)

\(P=\displaystyle\frac{1}{2}mv^2×nSl×\displaystyle\frac{1}{t}\)

\(v=\displaystyle\frac{eVt}{lm}\)と計算しているため、これを式へ代入しましょう。

\(P=\displaystyle\frac{m}{2}×\displaystyle\frac{e^2V^2t^2}{l^2m^2}\)\(×nSl\)\(×\displaystyle\frac{1}{t}\)

\(P=\displaystyle\frac{ne^2tS}{2ml}V^2\)

なお、\(R=\displaystyle\frac{2ml}{ne^2tS}\)であるため、式に代入しましょう。

\(P=\displaystyle\frac{V^2}{R}\)

こうして、1秒間で消費する運動エネルギーは\(P=\displaystyle\frac{V^2}{R}\)と計算できました。なお、得られた答えは電力\(P\)を得る公式です。

\(P=IV=I^2R=\displaystyle\frac{V^2}{R}\)

ここまでの計算というのは、電子一つを利用することにより、電力の公式を得るための計算です。もちろん、時間\(t\)をかけることによって電力量の公式を得ることも可能です。

内部エネルギーと仕事の関係ではなく、電子の運動エネルギーに着目することによっても電力の公式を得ることができます。どの方法であっても得られる答えは同じです。いずれにしても、物理では一つの物体（電子）に着目することで公式を導出することもできます。

ジュールの法則の原理を学ぶ

物理でジュールの法則を学ぶとき、多くのケースで公式の説明が乏しいです。そのためジュールの法則について、ほとんどの人が原理や詳細を学ぶことなく、公式を利用します。ただ、これでは何も学んでいないのと同じです。

内部エネルギーと仕事の関係を利用すれば、容易にジュール熱を得る公式を作れます。またオームの法則を利用すれば、ジュールの法則で利用される公式を導出できます。

なお、ジュール熱は電力量でもあります。電力量と電力の関係を学び、それぞれを計算できるようになりましょう。

応用問題にはなりますが、一つの電子に着目することでジュールの法則を得ることも可能です。いずれにしても、これまで学んだ知識とオームの法則を利用して、ジュール熱と電力量の計算を行えるようになりましょう。