波の干渉では、回折格子が関わる問題を出されます。光の経路差を計算することにより、波が強め合う場所を計算できます。
このとき、回折格子とは何かを学ばなければいけません。回折格子を利用する波の干渉というのは、ヤングの実験と似ています。計算方法は大きく異なるものの、ヤングの実験を学んでいる場合、回折格子を理解できます。
ただ回折格子には独自の特徴があります。回折格子では明線の間隔を計算できるものの、暗線条件がありません。この理由は何でしょうか。また回折格子に白色光を当てると、虹のように見える理由は何でしょうか。
計算方法や性質を知っていないと、回折格子に関する問題を解くことはできません。そこで、回折格子を用いるときの波の干渉条件をどのように計算すればいいのか解説していきます。
もくじ
回折格子とは何か:回折格子の原理と格子定数
まず、回折格子とは何かを学びましょう。回折格子を簡単に考えると、「ガラス板の片面に多数の溝をもつ物体」と理解しましょう。ただ溝は等間隔、かつ平行である必要があります。また、溝の間隔は非常に短く、回折格子には1mmの間に数百の溝が存在します。
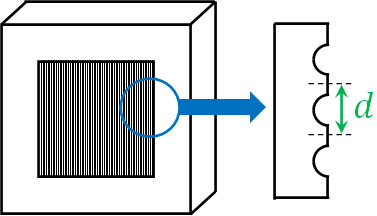
なお、溝の間隔を格子定数\(d\)といいます。
通常、光は直進します。ただ回折格子に光を当てると回折します。光が回折することにより、スクリーン上に複数の明線が表れます。

このように、光を回折させるアイテムが回折格子です。
回折格子はスリットと同じ役割となる
それでは、回折格子に入った光はどのように進むのでしょうか。前述の通り光は回折するわけですが、溝の部分については、光は通過することができません。そのため光が回折格子に入ると、光が通過する部分と遮られる部分が存在することになります。
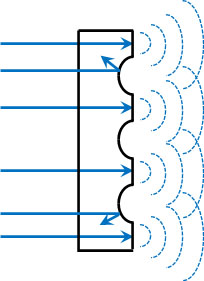
回折格子を利用するときの光の進み方を学ぶと、「回折格子はヤングの実験でのスリットと同じ役割である」とわかります。
ヤングの実験では、単スリットと複スリットを利用します。スリットを通過した光は波が広がりながら進みます。こうして波の干渉が起こり、明線と暗線がスクリーン上に作られます。回折格子はスリットと同じ機能を発揮するのです。
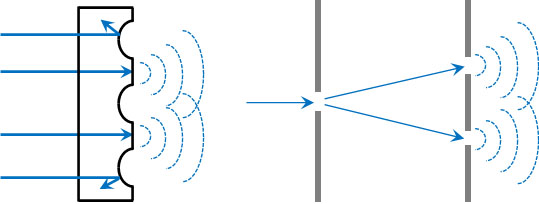
ヤング実験を学んでいる場合、回折格子の問題を解くことができます。回折格子で光の回折が起こる理由は、ヤングの実験で利用されるスリットのケースと同じだからです。つまり、光が回折するときの距離の差を計算することにより、波の干渉条件を得ることができます。
回折格子で明線を生じる条件
それでは、回折格子で明線を生じるときの条件を確認しましょう。光が回折して明線を生じるとき、光は一つの点に集まります。
ただ回折格子とスクリーンとの距離に対して、格子定数\(d\)の幅は非常に短いです。そのため、回折格子から角度θで発生される光は平行と考えることができます。
本当は平行ではないものの、平行の光と考えることによって計算することができます。光の回折で近似を利用するのは、ヤングの実験でも回折格子でも同様です。そこで、以下の図を作りましょう。
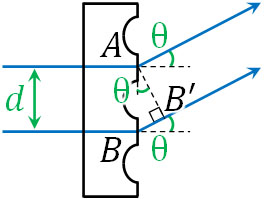
このように図を作ると、2つの光の距離の差はBB’であるとわかります。そのため明線を生じる条件を計算したい場合、BB’の距離を求めましょう。上図より、2つの光の経路差(BB’の距離)は\(dsinθ\)です。
また回折格子を利用するとき、同じ光を回折させます。そのため同位相の波が強め合うことになります。つまり距離BB’が半波長の偶数倍であれば、明線を生じます。そのため、波が強め合う条件(明線を生じる条件)は以下になります。
- \(dsinθ=\displaystyle\frac{λ}{2}×2m\) (\(m=0,1,2…\))
なお格子定数\(d\)は一定であり、回折後の光はすべて平行です。回折格子では、多くの光が回折します。ただすべての経路差は\(dsinθ\)です。そのため2つの波が強め合う場合、ほかの光線も同様に強め合うことになります。
ヤングの実験と違い、回折格子では細く明るい線になる
光の回折を利用し、スクリーン上に明線を生じるという意味では、ヤングの実験と回折格子の実験は似ています。それでは、ヤングの実験と回折格子の実験では何が違うのでしょうか。
ヤングの実験に対して、回折格子の実験では細く明るい線を作ることができます。以下のようなイメージです。

ヤングの実験で利用されるスリットは2つだけです。そのため線が明るくなるためには、2つの光がピッタリ重ね合わさる必要があります。同様に、暗くなるためには波の山と谷がぴったり重ね合わさる必要があります。
このとき、少し位置がずれた場合であってもぼんやり明るい状態(または暗い状態)となります。そのため、ヤングの実験で作られる光は太くなります。
一方、回折格子では2つのスリットではなく、非常に多くのスリットが存在することになります。そのため光がピッタリ重なる部分(波が強め合う部分)は非常に明るくなります。しかし少し場所がずれると、位相の異なる多くの波が重なることにより、合成波は0に近づきます。つまり、少し場所がずれると急に暗くなります。
暗線条件が回折格子で存在しない理由
回折格子の実験では、明線条件の計算問題を出されるものの、暗線条件を計算することはありません。この理由として、回折格子では暗線の場所があいまいだからです。
ヤングの実験では、2つのスリットのみを利用するため、明線と暗線が作られます。一方で回折格子の実験では、明線の場所は明らかであるものの、明線から少しずれると暗くなるため、暗線がわかりにくいのです。
回折格子の実験では、明線が表れている場所以外は暗いです。これが、回折格子で暗線条件がない理由です。
白色光を回折格子に当てると虹のように見える理由
なお白色光を回折格子に当てると、虹のように見えます。以下のように、スクリーン上に色が表れるのです。

真ん中はすべての可視光が集まるため、白色になります。ただその他の部分については、白色光の回折によって虹が表れます。この理由として、可視光は色によって波長が異なるからです。
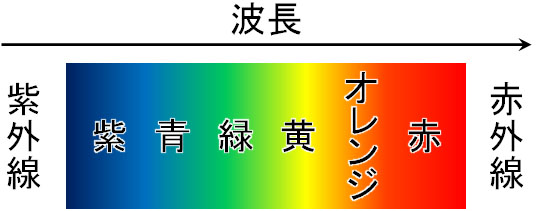
紫色では波長が短く、赤色では波長が長いです。可視光によって波長が異なるため、光が回折するとき、色によって強め合う位置が変化します。これが、白色光を回折格子に当てると虹が出現する理由です。
斜めに入射する光に関する練習問題
それでは、回折格子の実験に関する問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 以下の図のように斜め(角度θ)に波長\(λ\)のレーザー光を回折格子に入射させるとき、角度\(r\)のときに明線を生じる条件について、整数\(m\)を用いて表しましょう。なお、格子間隔は常に\(d\)であり、角度の大きさは\(r>θ\)です。

先ほどと同じように、経路差を確認しましょう。以下のように図を作ると、2つの光で点線の部分は共通部分とわかります。
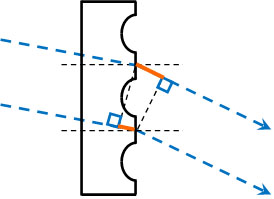
つまり、上図でオレンジ線が2つの光の距離の差に関与しています。波の干渉条件というのは、2つの経路差が重要です。そこで、それぞれのオレンジ線の長さをそれぞれ計算した後、引き算をしましょう。
図を作ると、以下のようになります。
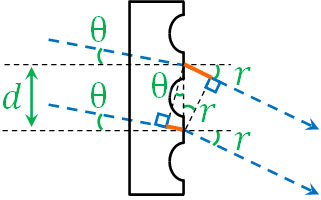
2つの光を比べると、一つの光は\(dsinr\)の距離があり、もう一方の光は\(dsinθ\)の距離があります。そのため、2つの光の経路差は\(dsinr-dsinθ\)です。\(r>θ\)であるため、\(dsinθ-dsinr\)ではなく、\(dsinr-dsinθ\)にしましょう。
こうして、2つの光について距離の差を得ることができました。波が強め合うとき、半波長の偶数倍になる必要があります。そのため、以下の式を作りましょう。
- \(dsinr-dsinθ=\displaystyle\frac{λ}{2}×2m\) (\(m=0,1,2…\))
こうして、回折格子へ斜めに入射する光の明線条件を計算できました。
反射型の回折格子ではさまざまな方向へ光が反射する
なお回折格子を学ぶとき、反射型の回折格子についても理解しましょう。基本的な考え方は同じであるものの、解き方を学んでいないと答えを得ることができません。
光が反射するとき、入射角と反射角が同じであることを既に学んでいると思います。ただ反射の法則は広い平面でなければ起こりません。
狭い平面で反射する場合、入射角と反射角は同じになりません。回折格子では多くの溝があり、光が反射する部分と反射しない部分が規則的に並んでいます。そのため光は狭い平面で反射することになり、反射型の回折格子では、反射後の光は同心円状に広がります。つまり、さまざまな方向に反射します。
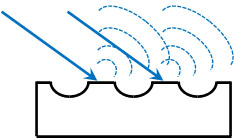
回折格子を利用する場合、光を透過させる場合であっても、反射させる場合であっても、光は回折します。光が回折するため、反射型の回折格子を利用すると明線が表れるようになります。
反射型の回折格子で経路差を得る計算
それでは、反射型の回折格子で経路差を計算してみましょう。回折格子へ斜めに入射する光の経路差を計算できる場合、反射型の回折格子の経路差も計算できます。以下の問題の答えは何でしょうか。
- 以下の図のように角度θにて、斜めに波長\(λ\)のレーザー光を回折格子に入射させるとき、反射角度\(r\)のときに明線を生じる条件について、整数\(m\)を用いて表しましょう。なお、格子間隔は常に\(d\)であり、角度の大きさは\(r>θ\)です。
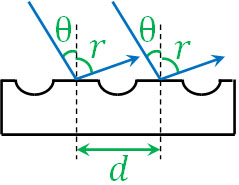
2つの光の経路差がどの部分なのかを考えましょう。以下のように図を作ると、点線の部分は長さが共通しています。
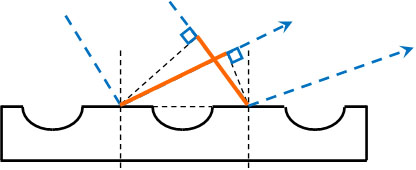
一方、オレンジの部分に違いを生じています。そこで、それぞれのオレンジ線の長さを計算し、差を求めましょう。2つの光の経路差が半波長の偶数倍であれば、2つの波は互いに強め合います。
そこで、以下の図を作りましょう。
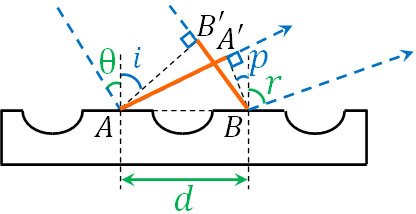
図より、以下がわかります。
- \(θ+i=90°\)
- \(i+∠BAB’=90°\)
そのため、\(∠BAB’=θ\)とわかります。また図より、以下がわかります。
- \(r+p=90°\)
- \(p+∠ABA’=90°\)
そのため、\(∠ABA’=r\)とわかります。つまり、それぞれのオレンジ線の長さは\(dsinθ\)と\(dsinr\)になります。角度の大きさは\(r>θ\)であるため、2つの光の経路差は以下になります。
- \(dsinr-dsinθ\)
つまり、明線条件は以下の式になります。
- \(dsinr-dsinθ=\displaystyle\frac{λ}{2}×2m\) (\(m=0,1,2…\))
反射型の回折格子で2つの光の経路差を計算するとき、どの辺の長さを計算すればいいのか認識しましょう。また角度がどこに該当するのかを確認し、引き算をすることによって経路差を得るといいです。
回折格子の原理と特徴、計算方法を学ぶ
波の干渉で重要な内容の一つが回折格子です。回折格子の実験はヤングの実験と似ており、回折によってスクリーン上に明線が表れます。
ただヤングの実験と回折格子の実験には違いがあります。ヤングの実験では明線と暗線の条件があります。一方で回折格子の実験では、暗線の条件がなく、明線の条件のみ計算することになります。
そこで2つの光の経路差を計算し、明線が表れるときの条件を出しましょう。同位相の波が強め合うため、回折格子の実験では、半波長の偶数倍になれば明線が表れます。このとき、斜めに入射する光や反射型の回折格子の計算問題を解けるようになりましょう。
波の干渉条件に関する応用問題が回折格子です。回折格子は重要な学習内容の一つであるため、どのように2つの光の経路差を計算すればいいのか理解しましょう。