私たちは物理で重心を学びます。剛体の回転では、力のモーメントを考慮する必要があります。力のモーメントがゼロになる点が重心です。数学で学ぶ重心と物理で学ぶ重心はまったくの別物であり、分けて考える必要があります。
なお物理の教科書には、重心の公式が記載されています。ただ重心の公式を覚える必要はなく、公式を覚えると応用問題を解けなくなります。
それよりも、重心の公式がなぜ成立するのかを学ばなければいけません。これにより、物体の重心の意味がわかります。
それでは、どのように重心を計算すればいいのでしょうか。重心の概念や公式の意味、計算方法を解説していきます。
もくじ
力のモーメントが0になる部分が重心
まず、物理で学ぶ重心とは何でしょうか。重心というのは、力がつり合う点を指します。例えば以下の状態では、2つの重りはバランスが取れて静止しています。
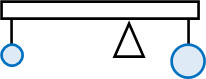
このときの支点(物体を支えている点)が重心です。重心とは、言い換えると力のモーメントが0になる点を指します。
棒や板、直方体など、物体によって形はさまざまです。こうした物体には重心があり、一つの点(重心)に乗せることによって、傾くことなくその場で静止します。重心では力のモーメントが0であるため、回転する力が働かないからです。
重心の本質を理解するとき、力のモーメントが0になる点が重心であることを知るのは必須です。
物理での重心の公式は覚えなくていい
なお物理の教科書では、必ず重心の公式が提示されます。質量がそれぞれ\(m_1,m_2,…\)である複数の物体があるとき、重心の座標\(x_G\)を得る公式は以下になります。
- \(x_G=\displaystyle\frac{m_1x_1+m_2x_2+…}{m_1+m_2+…}\)
ただ、この公式を覚えてはいけません。事実、応用問題が出されると公式を利用できなくなります。また、説明の下手な人ほど公式を覚えさせ、公式に値を代入することを推奨します。そうではなく、なぜこの公式が成り立つのかを理解しましょう。
先ほど解説した通り、力のモーメントが0になる点が重心です。そこで、力のモーメントを利用して式を作りましょう。
例えば下図の状態で静止している物体について、\(x\)軸の左側に任意の点\(x_0=0\)を作ります。
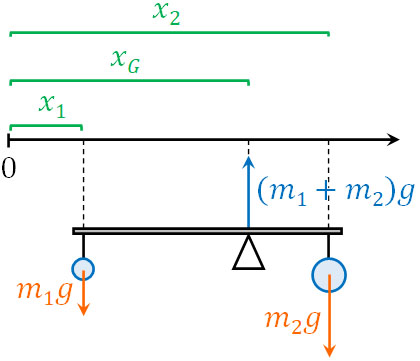
\(x_0\)を基準にするとき、重心\(x_G\)はどこでしょうか。\(x_0\)を支点にすると、2つの重りによって下向きの力が加わっています。一方、重心\(x_G\)では上向きの力が加わっています。そのため、力のモーメントの式は以下のようになります。
\((m_1+m_2)g·x_G=m_1g·x_1+m_2g·x_2\)
また、式を変形すると以下のようになります。
\(x_G=\displaystyle\frac{m_1x_1+m_2x_2}{m_1+m_2}\)
こうして、先ほどの公式と同じ形にすることができました。なお重りの数が増えたとしても、力のモーメントが0になるように式を作ればいいのでやり方は同じです。重心の本質を学べば、なぜ重心の公式を覚える必要がないのか理解できます。
物理の重心では、出発点を決めなければいけない
先ほどの計算方法を確認すればわかる通り、出発点\(x_0\)が重要です。重心の位置は変わらないものの、任意の点\(x_0\)がどこなのかによって座標が変わります。言い換えると、\(x_1\)と\(x_2\)の長さが変わります。
そのため物理で重心の問題を解く場合、スタート地点\(x_0\)がどこになるのか把握しましょう。例えば以下のように、出発点\(x_0\)を重りの場所と一致させる場合はどのように力のモーメントを計算すればいいでしょうか。
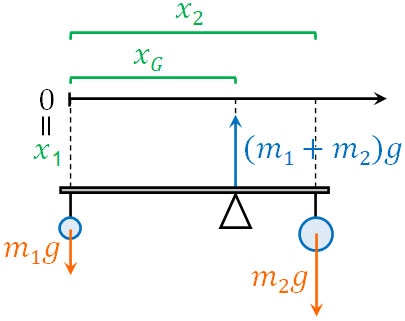
この場合、\(x_0=x_1=0\)になります。そこで、\(x_1\)を基準にするときの力のモーメントを作りましょう。以下のようになります。
\((m_1+m_2)g·x_G=m_2g·x_2\)
\(x_1\)は出発点であるため、\(x_1=0\)です。また重心ではすべての重さが加わっているため、質量は\(m_1+m_2\)となります。出発点と重心の距離は\(x_G\)であり、上向きの力が加わっています。
それに対して、もう一方の重りの質量は\(m_2\)、出発点との距離は\(x_2\)であり、下向きの力が加わっています。そのため、先ほど記した式を作ることができます。そこで式を変形すると以下のようになります。
\(x_G=\displaystyle\frac{m_2x_2}{m_1+m_2}\)
こうして、\(x_1=0\)とする場合の重心を計算できました。重心の位置は同じであるものの、スタート地点をどこにするのかによって式が変化し、計算過程を簡単にできます。スタート地点が変わると、当然ながらスタート地点と重心との距離は変化するのです。
数学で学ぶ重心と物理で学ぶ重心は異なる
なお数学で学ぶ重心では、公式を覚えていないと問題を解くことができません。数学と物理では、重心の概念が大きく異なるのです。
物理は世の中の自然現象を取り扱います。そのため、物体に重さがあることを考慮して式を作らなければいけません。
一方で数学の図形で学ぶ重力では、物体の重さを考慮しません。数学の場合、すべての物体は質量が1と仮定して計算します。
なお、数学では質量がすべて1であるため、ここまで解説した公式に質量1を代入すると数学で学ぶ重心の公式になります。いずれにしても、数学と物理では重心の計算方法が大きく異なる事実を理解しましょう。
L字物体に存在する重心の練習問題
それでは、物理での重心を計算してみましょう。以下の問題の答えは何でしょうか。
- 下図のように、L字の棒があります。棒の重心はどこですか。

棒の上には重心がありません。重心というのは、物体上に存在するとは限らないのです。そこで、L字方の棒に質量0の透明で硬いフィルムが以下のように存在すると仮定しましょう。

この場合、フィルム上のどこかにL字棒の重心があります。
重心では力のモーメントが0になります。また図を確認すると、左下の座標が\(0,0\)となっています。そこで、この点を出発点にして力のモーメントの式を作りましょう。
問題文にある図では、座標\((0,0)\)を支点として、座標\((0,1)\)に質量\(m\)、座標\((2,0)\)に質量\(2m\)の物体が存在すると考えることができます。「棒や板などの重さ」は中心を基準とするため、座標は\((0,1)\)と\((2,0)\)になるのです。
このとき、どこが重心か不明であるものの、ひとまず重心の座標\((x_G,y_g)\)を設定しましょう。また重心を求めるとき、\(x\)座標と\(y\)座標を分けて計算する必要があります。そこで\(x\)座標での力のモーメントの式と\(y\)座標での力のモーメントの式を作りましょう。
このとき、重心に置くことでL字棒が静止している場合、\(x\)座標では以下の図を作ることができます。
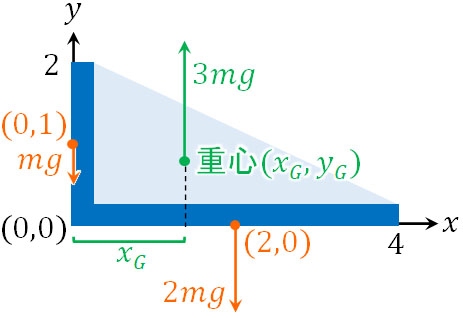
また、\(x\)座標での力のモーメントの式は以下のようになります。
\(3mg·x_G=2mg×2\)
\(x_G=\displaystyle\frac{4}{3}\)
こうして、\(x\)座標の重心は\(\displaystyle\frac{4}{3}\)とわかります。
次に\(y\)座標の重心を計算しましょう。どの角度であっても重心は変化しません。つまり、計算しやすいように自由に角度を動かして重心を計算できます。そこで理解しやすいように、\(y\)座標を地面に平行にして、\(x\)座標を天井に向けましょう。そうすると、図は以下のようになります。
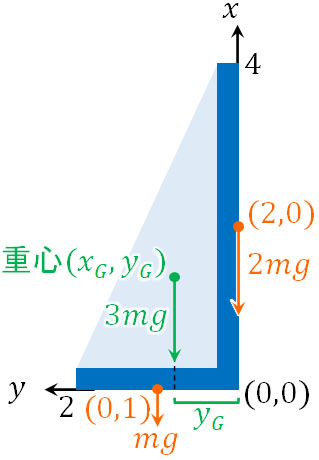
地面と平行になっているのは\(y\)座標であるため、\(y\)座標に着目して力のモーメントの式を作りましょう。そうすると、以下のようになります。
\(3mg·y_G=mg×1\)
\(y_G=\displaystyle\frac{1}{3}\)
こうして、\(y\)座標の重心は\(\displaystyle\frac{1}{3}\)とわかりました。つまり、重心の座標は\(\left(\displaystyle\frac{4}{3},\displaystyle\frac{1}{3}\right)\)です。
重心の公式を利用していませんが、答えを得ることができます。またこの方法で式を作れば、すべての応用問題を解くことができます。物理で重心を学ぶとき、公式を覚えることに意味はなく、物理現象の本質を学ぶことのほうが重要です。
切り抜き図形での重心の計算
次に、切り抜き図形での重心を求めましょう。長方形や円の図形を切り抜くとき、重心がどこに存在するのか計算するのは応用問題に当たります。以下の問題の答えは何でしょうか。
- 円の一部を切り取った以下の図形の重心を求めましょう。なお、点Oは大きい円の中心です。
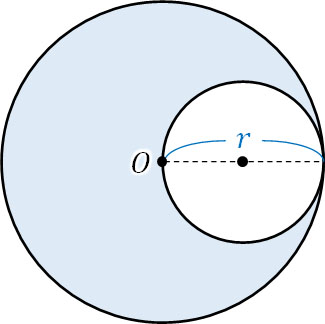
切り抜きの図形では、公式を利用して問題を解くことができません。そのため、物理で重心を学ぶときは力のモーメントを利用して式を作るべきなのです。
まず、それぞれの円の重さを計算しましょう。切り抜いた円(小さい円)を元に戻せば、大きい円となります。
また質量の比は面積比と同じです。切り抜かれた円の面積は\(\displaystyle\frac{3}{4}πr^2\)であり、切り抜いた円(小さい円)の面積は\(\displaystyle\frac{1}{4}πr^2\)です。そのため、半径を利用して面積比を求めると以下のようになります。
- 切り抜かれた円:切り抜いた円(小さい円)\(=3:1\)
例えば切り抜いた円(小さい円)の質量が\(m\)の場合、切り抜かれた円の質量は\(3m\)です。
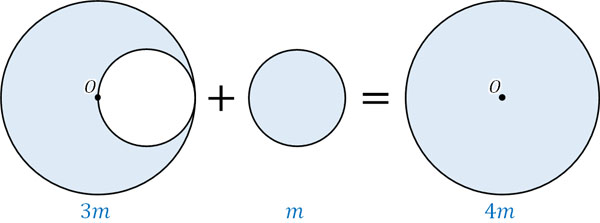
力のモーメントを計算するためには質量が必須なので、このようにしてそれぞれの円の質量を計算しましょう。
・重心の計算を行う
まず、重心がどこにあるのか予測しましょう。円の右側がくり抜かれているため、円の右側は軽くなっています。言い換えると、点Oを支点にすると左に傾いて倒れます。そこでバランスを保つためには、重心は以下のオレンジ線のどこか(点Oの少し左)に存在すると予想できます。
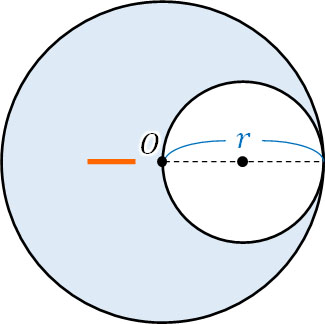
物理では、実際に現象が起こる場面を想像しなければ問題を解くのが難しいです。そのため、このように重心の場所がどこか推測しましょう。
なお切り抜かれる前の円では、重心は明らかに点Oです。つまり切り抜かれる前では、点Oを支点にすると力のモーメントは0になります。
そのため切り抜かれた円と切り抜いた円(小さい円)を足す場合、重心が点Oにならなければいけません。言い換えると、点Oを支点とするとき、切り抜かれた円の力のモーメントと切り抜いた円(小さい円)の力のモーメントを足すと0になります。
この関係を利用して力のモーメントの式を作りましょう。仮に左回りを正とすると、右回りの力は負になります。この場合、力のモーメントの式は以下のようになります。
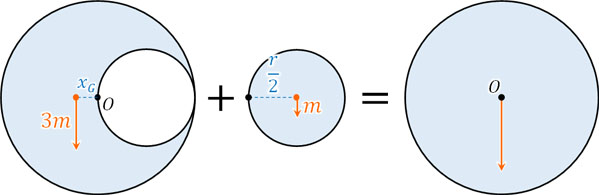
\(3m·x_G-m·\displaystyle\frac{r}{2}=0\)
\(3m·x_G=m·\displaystyle\frac{r}{2}\)
\(x_G=\displaystyle\frac{r}{6}\)
こうして、重心は点Oから左に\(\displaystyle\frac{r}{6}\)の位置にあるとわかります。
負の質量をもつと考えて計算する
参考までに、先ほどの問題では別解もあります。別解では、負の質量を考えましょう。重りをつけると、当然ながら質量は重くなります。一方で物体を切り取ると、質量は軽くなります。そこで物体を切り取るとき、「物体は負の質量をもつ」と考えるのです。
切り取る前の円から小さい円を引くと、問題文にある図形を作ることができます。つまり、以下のように力のモーメントを考えます。
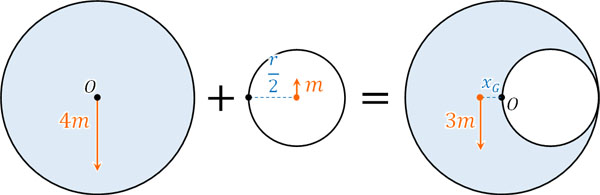
元の大きい円に対して、小さい円を引くと、新たな円では重心\(x_G\)で力のモーメントがゼロになります。言い換えると回転する力がなく、バランスが取れることによってつり合います。
これはつまり、\(x_G\)を支点とするとき、元の大きい円と小さい円の力のモーメントが同じであることを意味します。そこで\(x_G\)を支点(距離0)として、以下の図を作りましょう。
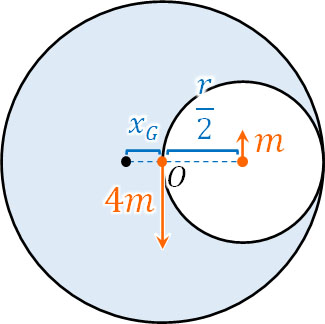
この図を利用して力のモーメントの式を作ると、以下のようになります。
\(4m·x_G=m\left(x_G+\displaystyle\frac{r}{2}\right)\)
\(4x_G=x_G+\displaystyle\frac{r}{2}\)
\(3x_G=\displaystyle\frac{r}{2}\)
\(x_G=\displaystyle\frac{r}{6}\)
こうして、先ほどと同じ答えを得ることができます。物質を切り抜くとき、負の質量をもつことを学べば、この性質を利用することによっても答えの計算が可能です。
公式を利用せず、座標と力のモーメントを利用して重心を計算する
物理では公式を覚えないほうがいいケースは多いです。理由としては、公式を覚えても応用問題を解けない場合が多いからです。物理で学ぶ重心は公式を利用してはいけない学習内容の一つです。
重心は決まっており、動くことはありません。重心で支えれば、必ず力のモーメントは0になります。この本質を学べば、力のモーメントを利用して重心の計算をするべきとわかります。またこの方法であれば、すべての応用問題を解けます。
なお重心を探すとき、出発点がどこになるのか見極めましょう。計算しやすい場所を出発点に設定すれば、力のモーメントの式を作りやすいです。
物理の問題を解くためには、公式を覚えるのではなく、物理現象が起こる理由を学びましょう。そうすれば、物理の計算が可能になります。






