有機化学では、立体配座がどのようになっているのか理解しなければいけません。有機化合物は平面ではなく、立体構造を有しているからです。立体化学を学ぶことで、化学反応が進行するかどうかを予測できることは多いです。
また同じ分子であっても、どのような立体配座になるのかが違ってきます。置換基がどの位置に存在するのかによってエネルギーが異なるのです。
立体化学で最初に学ぶものの一つがアルカンの立体配座です。アルカンの立体化学ではNewman投影式(ニューマン投影式)を利用します。軸の回転に着目して、分子の様子を記すのがニューマン投影式です。
ニューマン投影式を利用することで、アルカンがどのような立体配座になるのか理解できるようになります。ここでは、立体化学の初歩であるアルカンの立体構造について解説していきます。
もくじ
Fischer投影式とNewman投影式の関係
有機化合物の構造式を書くときには、さまざまな方法があります。その中でも、Fischer投影式(フィッシャー投影式)が利用されることはよくあります。
キラル炭素(不斉炭素原子)があったとしても、分子の構造を二次元にて書き記す方法がフィッシャー投影式です。
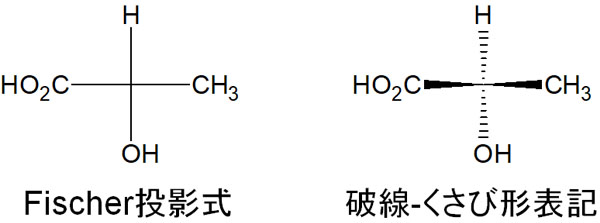
キラル中心がある場合、頻繁に用いられる手法が破線-くさび形表記です。平面に分子を記すものの、破線で記すと置換基は奥に存在することを意味します。くさび形では、手前に置換基が存在します。一方、結合をすべて平面で記すのがフィッシャー投影式です。
・Fischer投影式(フィッシャー投影式)では立体配座が分からない
ただフィッシャー投影式には、分子の立体配座がまったく分からないという欠点があります。そのため、立体化学を考えるときはNewman投影式(ニューマン投影式)が頻繁に利用されます。
同じ分子で置換基の位置がどのようになっているのか表すのがニューマン投影式です。例えば、以下のようになります。
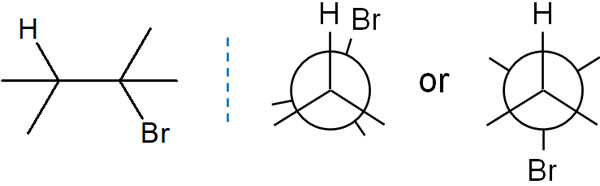
フィッシャー投影式では無理であっても、ニューマン投影式であれば、分子がどのような立体配座を分子が取るのかを理解できるようになります。
アルカンの立体配座をニューマン投影式で考える
立体化学でアルカンがどのように機能するのかについては、ニューマン投影式を使わなければ理解することはできません。それでは、ニューマン投影式はどのように利用すればいいのでしょうか。まず、Fischer投影式(フィッシャー投影式)を立体で考えるようにしましょう。
すべての分子は立体的です。ニューマン投影式は分子構造を立体的に考える手法の一つです。またニューマン投影式に特徴的なこととして、分子を横から見ます。
例えば、エタンのニューマン投影式は以下のようになります。
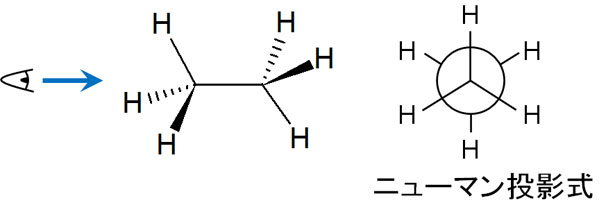
C-C結合(炭素同士の結合)を中心にして、周囲にどのような置換基が存在するのか確認するのがニューマン投影式です。
ニューマン投影式の中心では、2つの炭素原子が重なっています。軸の横側から見たときの様子がニューマン投影式です。この記載方法を理解することで、分子の立体配座によってエネルギーの違いがどのようになっているのか理解できるようになります。
単結合(σ結合)では軸が回転し、二面角を考慮する
なぜ、ニューマン投影式を考える必要があるのでしょうか。これは、単結合(σ結合)では軸が自由に回転するからです。例えばエタンでは、以下のようにC-C結合の軸が回転します。

二重結合や三重結合では、軸の回転はありません。そのため、二重結合を有する化合物についてニューマン投影式を書くことはありません。ニューマン投影式は軸の回転による立体配座がどうなっているのかを考えるためのものであり、軸の回転がない二重結合や三重結合でニューマン投影式を利用する意味はないのです。
軸が回転する単結合では、二面角を考える必要があります。ニューマン投影式のように、軸の横から分子をみると、二面角によるひずみを生じることがあります。
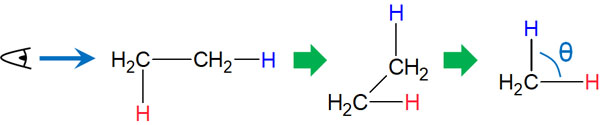
二面角の理想的な角度(θ)は60°です。しかし場合によっては、二面角が0°になることもあります。軸は自由に回転するため、二面角の角度は状況によって異なるのです。ニューマン投影式を利用すれば、二面角ひずみがどのようになっているのか理解しやすくなります。
ニューマン投影式とは、二面角ひずみの様子を理解するためのツールだと考えましょう。
重なり形配座より、ねじれ形配座が安定構造になる
それでは、分子の軸が回転することで二面角ではどのようなひずみを生じるのでしょうか。エタンの例で考えてみましょう。
まずエタンのC-C結合が回転することで、二面角(θ)が60°になるケースと0°になるケースを考えます。この場合、二面角が60°になるときをねじれ形配座(スタッガード)といいます。一方、二面角が0°になるときを重なり形配座(エクリプスド)といいます。
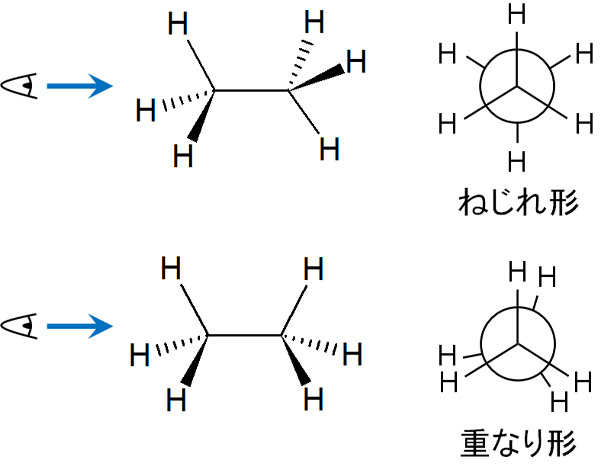
軸の回転により、ねじれ形と重なり形の2つの形になることができます。ちなみに重なり形について、実際には完全に重なっています。ただニューマン投影式で重ねて書くと、後ろの炭素原子に結合している置換基の様子が分からないため、このように少しずらして記載するのが一般的です。
そうしたとき、ねじれ形と重なり形ではどちらのほうが安定なのでしょうか。分子は重なり形ではなく、ねじれ形のほうが安定した構造となります。
軸の回転により、ポテンシャルエネルギーに違いを生じる
重なり形で不安定となる理由には、電子の反発が関与しています。電子を共有することで分子は共有結合を作ります。そうしたとき、マイナスの電荷を有している電子は反発します。
重なり形では、結合に関与している電子が互いに反発するため、不安定な状態になります。二面角が0°だと、ひずみを生じることでエネルギーが大きくなるのです。
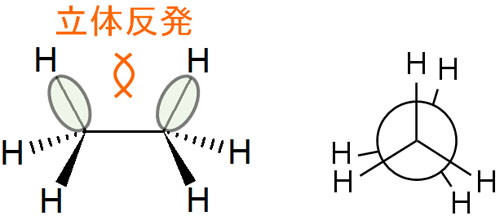
そのため軸は自由に回転できるものの、二面角が0°なのか60°なのかによって分子内のエネルギーが高くなったり低くなったりします。
二面角が0°だと、ポテンシャルエネルギーが高いです。一方で二面角が60°になると、ポテンシャルエネルギーが低くなります。エネルギー図に表すと以下のようになります。

ニューマン投影式で二面角を表すと、このように角度によってポテンシャルエネルギーが異なることを理解しましょう。
ブタンではアンチ形とゴーシュ形で安定構造が異なる
それではエタンではなく、より多くの置換基を有する化合物ではどうなのでしょうか。これについて、ブタンが頻繁に例として利用されます。
プロパンはエタンと同じ形のポテンシャルエネルギー図となります。そのため、エタンもプロパンも立体配座によるエネルギーの違いは同じです。一方でブタンでは、より安定構造が複雑になります。
ブタンについてニューマン投影式で構造を書く場合、ねじれ形配座(スタッガード)では以下の2通りを考えることができます。
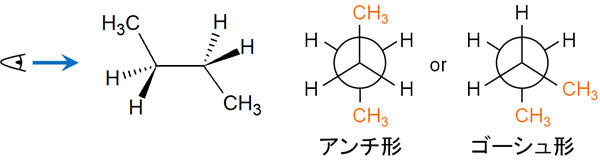
同じねじれ形配座(スタッガード)であっても、一方ではメチル基が180°の位置にある構造を書くことができます。この立体配座をアンチ形といいます。
一方でメチル基が60°の位置になるニューマン投影式を書くこともできます。この立体配座をゴーシュ形といいます。
アンチ形とゴーシュ型では、ポテンシャルエネルギーに違いがあるのでしょうか。これについて、ゴーシュ型ではエネルギーが高くなります。理由としては、メチル基が近くに存在するので立体的に反発するからです。
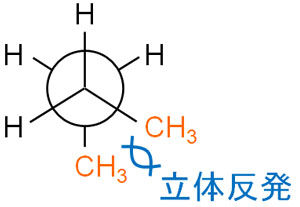
立体化学で安定性を考えるとき、立体障害の状態を確認しなければいけません。
アンチ形ではメチル基が180°の位置に存在しているため、立体障害はありません。一方でゴーシュ形では、メチル基同士が60°の位置にあるので立体反発します。そのため、ゴーシュ形はアンチ形に比べてひずみが大きく、エネルギーが高いです。ゴーシュ形よりも、アンチ形のほうが安定です。
スタッガードとエクリプスドは置換基でエネルギーが違う
同じことはねじれ形配座(スタッガード)だけでなく、重なり形配座(エクリプスド)にもいえます。スタッガードでメチル基の位置が違うことでエネルギーが異なっていたのと同じように、エクリプスドでも置換基の場所でエネルギー状態が違います。
重なり形配座(エクリプスド)では、以下の2つの立体配座を考えることができます。
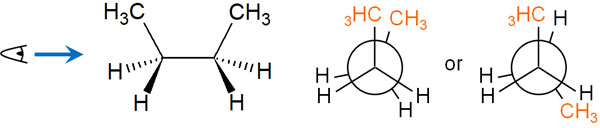
立体障害を考えるとき、メチル基が重なっている形は非常にエネルギー状態が高く、不安定だといえます。メチル基は水素原子に比べて、形が非常に大きいです。大きい置換基が最も近くにある状態だと、高エネルギーになります。
一方で重なり形配座(エクリプスド)の中でも、メチル基が離れて存在している場合はエネルギー状態が低くなります。もちろん結合が重なっているため、エネルギー状態が高く不安定であるのは変わりません。ただメチル基同士が重なっている状態に比べると、安定な状態だといえます。
メチル基の位置で異なるアルカンのポテンシャルエネルギー図
これらブタンのニューマン投影式を考えるとき、C-C軸(炭素の単結合)が回転することでポテンシャルエネルギーはどのようになるのでしょうか。安定(または不安定)な状態をエネルギー図で記すと、以下のようになります。
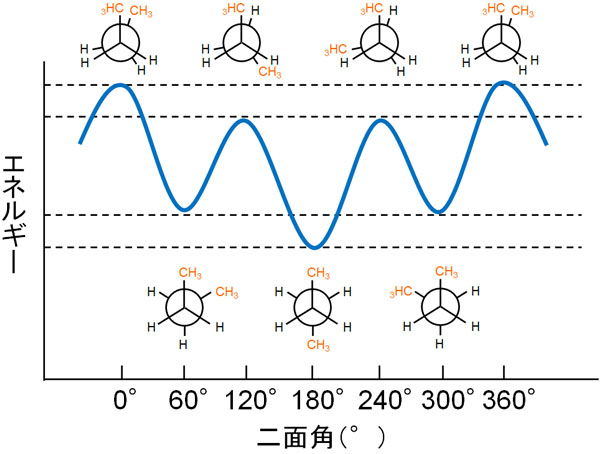
どのような立体配座となっているのかによって、このようにブタンのポテンシャルエネルギーは異なります。
ねじれ形配座(スタッガード)ではエネルギーが低くなって安定です。ただ上図のように、メチル基がゴーシュ形の場合、エネルギーは少し高いです。一方でメチル基がアンチ形では、立体障害がないのでエネルギーは最も低く安定です。
重なり形配座(エクリプスド)では、メチル基が重なる部分で最も不安定です。それに対して、メチル基が重ならない場合は少しだけエネルギーが低くなります。
立体化学でのエネルギーを把握する
多くの場合、有機化学では平面にて構造式を記します。例えばFischer投影式(フィッシャー投影式)を利用すれば、立体異性体があったとしても平面で構造式を記載できます。
しかし分子はどれも立体的です。また二重結合や三重結合では関係ないですが、単結合では軸が自由に回転します。そのため、どのような立体配座になるのかによって分子が有するエネルギーが異なります。そうしたとき、分かりやすく考えるためにNewman投影式(ニューマン投影式)が利用されます。
ニューマン投影式で最初に考えるべきは重なり形配座(エクリプスド)とねじれ形配座(スタッガード)です。理想的な二面角の角度は60°であり、ここからずれるとエネルギーが高くなって不安定です。
それだけでなく、より多くの置換基がある場合はアンチ形とゴーシュ形があることを理解しましょう。これらのエネルギーが違うことを学べば、分子がどのような形をしているのかについて、より詳しく把握できるようになります。また、合成反応の起こりやすさを推測できます。






