図で\(x\)座標と\(y\)座標を表すとき、\(t\)を用いることがあります。平面図形に関する問題を解くとき、\(t\)を用いて答えを得たことは何度もあるはずです。
このように、\(t\)を利用して\(x\)座標と\(y\)座標を表す方法が媒介変数表示です。媒介変数表示を利用することによって曲線を表現でき、ベクトルや微分・積分で計算するときも利用できます。
なお媒介変数表示を利用して表記するとき、さまざまな表記法があります。また、媒介変数表示では\(x\)や\(y\)の変数に注意しなければいけないことが多く、式を作るときに範囲を確認しましょう。
すでに媒介変数表示を利用して計算問題を解いたことは何度もあるはずです。そこで、どのように媒介変数表示を利用して図形の問題を解けばいいのか解説していきます。
もくじ
媒介変数表示は何通りも方法がある
\(x\)や\(y\)などの変数について、別の変数で表す方法を媒介変数表示といいます。媒介変数表示では、多くのケースで\(t\)または\(θ\)を利用します。
媒介変数表示を利用するとき、一つの式について無数の表現法があります。例えば\(y=2x\)について、\(t\)を用いて\(x\)と\(y\)を表しましょう。\(x=3t\)とする場合、\(x=3t\)を\(y=2x\)に代入すると\(y=6t\)です。こうして、\(y=2x\)を以下のように表すことができます。
- \(x=3t\)
- \(y=6t\)
また\(x=\displaystyle\frac{t}{2}\)とする場合、\(x=\displaystyle\frac{t}{2}\)を\(y=2x\)に代入すると\(y=t\)です。
- \(x=\displaystyle\frac{t}{2}\)
- \(y=t\)
これも\(y=2x\)を表す媒介変数表示です。このように確認すると、同じ式であっても媒介変数表示を用いるとき、表現方法が無数に存在する理由がわかります。
円と楕円の媒介変数表示
前述の通り、媒介変数表示の方法は無数に存在します。その中でも、代表的な媒介変数表示を学びましょう。ここで解説する方法が唯一の媒介変数表示ではないものの、最も利用される媒介変数表示の方法を理解するのです。
まず、最も理解しやすい円の媒介変数表示を確認しましょう。円では\(θ\)を利用して\(x\)と\(y\)を表すことがひんぱんにあります。半径を\(r\)とすると以下のように表現できます。
- \(x=rcosθ\)
- \(y=rsinθ\)
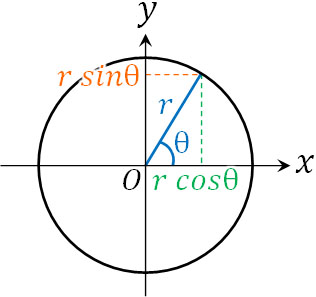
三角関数を学んでいる場合、説明しなくてもこのように表現できる理由がわかると思います。
・楕円の媒介変数表示
次に、楕円の代表的な媒介変数表示を学びましょう。\(a>b>0\)のとき、楕円の\(x\)軸を\(x=acosθ\)と表しましょう。下図のように半径\(a\)の円を考えると、なぜ楕円の\(x\)軸が\(x=acosθ\)と表せるのかわかります。
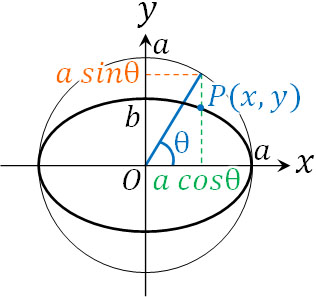
またこの楕円では、円に対してたての方向(\(y\)軸方向)に長さが\(\displaystyle\frac{b}{a}\)倍となっています。そこで、半径\(a\)の円上に存在する点について、\(y\)の媒介変数表示を\(\displaystyle\frac{b}{a}\)倍しましょう。
半径\(a\)の円では、\(y\)の媒介変数表示は\(y=asinθ\)です。これを\(\displaystyle\frac{b}{a}\)倍すると、楕円での媒介変数表示を得ることができます。
\(y=asinθ×\displaystyle\frac{b}{a}\)
\(y=bsinθ\)
こうして、以下のように楕円の媒介変数表示を計算できます。
- \(x=acosθ\)
- \(y=bsinθ\)
媒介変数を用いた楕円の表記法はほかにも無数に存在するものの、これが代表的な楕円の媒介変数表示です。
放物線と双曲線の媒介変数表示
次に、放物線の代表的な媒介変数表示を学びましょう。放物線の方程式は\(y^2=4px\)です。ここで、\(x=pt^2\)としましょう。理由としては、\(x=pt^2\)を\(y^2=4px\)へ代入すると\(y=2pt\)となり、計算しやすいからです。
\(x=pt\)としてもいいですが、この場合は\(y=2p\sqrt{t}\)となってしまいます。媒介変数表示を利用するとき、計算が容易であるほど優れるため、放物線では\(x=pt^2\)とするのが代表的な媒介変数表示の方法となります。
- \(x=pt^2\)
- \(y=2pt\)
媒介変数表示を覚えてはいけません。そうではなく、なぜ上記の式が主な媒介変数表示になるのか理由を学びましょう。
・双曲線の媒介変数表示
楕円や放物線と同様に、覚えてはいけない媒介変数表示が双曲線です。双曲線を表す主な媒介変数表示は以下になります。
- \(x=\displaystyle\frac{a}{cosθ}\)
- \(y=btanθ\)
この式を得るため、三角関数の公式の一つである\(tan^2θ+1=\displaystyle\frac{1}{cos^2θ}\)を変形しましょう。
\(tan^2θ+1=\displaystyle\frac{1}{cos^2θ}\)
\(\displaystyle\frac{1}{cos^2θ}-tan^2θ=1\)
この式を見てわかる通り、放物線の方程式\(\displaystyle\frac{x^2}{a^2}-\displaystyle\frac{y^2}{b^2}=1\)と形が同じです。また\(\displaystyle\frac{x^2}{a^2}=\displaystyle\frac{1}{cos^2θ}\)、\(\displaystyle\frac{y^2}{b^2}=tan^2θ\)となるため、上記の媒介変数表示が成り立ちます。
媒介変数表示を用いて図形を表す
それでは、媒介変数表示を式へ変形できるようになりましょう。方法は簡単であり、\(t\)や\(θ\)を消せばいいです。それでは、以下の式で表される点P\((x,y)\)はどのような曲線を描くでしょうか。
- \(x=2sinθ+1\)
- \(y=3cosθ-2\)
\(sin^2θ+cos^2θ=1\)に代入しましょう。
\(sin^2θ+cos^2θ=1\)
\(\displaystyle\frac{(x-1)^2}{4}+\displaystyle\frac{(y+2)^2}{9}=1\)
こうして、楕円の方程式を得ることができました。
\(x\)や\(y\)の変数に注意して式を作る
それでは、もう少し複雑な問題を解いてみましょう。\(t\)が媒介変数であるとき、以下の式で表される曲線はどのような図形でしょうか。
- \(x=3^t+3^{-t}+2\)
- \(y=3^t-3^{-t}-1\)
\(x=3^t+3^{-t}+2\)を\(x-2=3^t+3^{-t}\)に変形し、\(y=3^t-3^{-t}-1\)を\(y+1=3^t-3^{-t}\)へ変形し、二乗しましょう。
- \((x-2)^2=3^{2t}+2+3^{-2t}\)
- \((y+1)^2=3^{2t}-2+3^{-2t}\)
次に、以下のように引き算をすることで\(t\)を消しましょう。
\((x-2)^2-(y+1)^2=4\)
\(\displaystyle\frac{(x-2)^2}{4}-\displaystyle\frac{(y+1)^2}{4}=1\)
こうして、双曲線の方程式を得ることができました。なお媒介変数を利用するとき、\(x\)と\(y\)の変域にも気を付けましょう。
\(3^t>0\)と\(3^{-t}>0\)より、相加平均・相乗平均を利用すると以下のように計算できます。
\(3^t+3^{-t}≧2\sqrt{3^t·3^{-t}}\)
\(3^t+3^{-t}≧2\)
\(x=3^t+3^{-t}+2\)であるため、\(x≧4\)です。そのため、答えは\(\displaystyle\frac{(x-2)^2}{4}-\displaystyle\frac{(y+1)^2}{4}=1\)について、\(x≧4\)の部分です。
媒介変数表示を用いて式を表す
式を表すとき、\(x\)成分と\(y\)成分を分けて式を表すことができます。一つの変数をほかの変数で記すことにより、複雑な式であっても単純な式になることがあります。
このとき、媒介変数表示には無数の表現方法があります。その中でも円や楕円、放物線、双曲線で代表的な媒介変数表示を学びましょう。暗記しても意味がなく、代表的な媒介変数表示を得られるようにする必要があります。
なお媒介変数表示を利用して式を作るとき、\(x\)と\(y\)の範囲に注意しましょう。公式や相加平均・相乗平均などを利用して、範囲に制限がないかどうかを確認するのです。
媒介変数表示を利用することにより、式をほかの方法によって表すことができます。そこで媒介変数表示の性質を学び、計算できるようになりましょう。






