漸化式に関する問題を解くとき、特性方程式を利用することが多いです。αを利用することにより、漸化式を変形して数列の一般式を得るのです。
ただ、多くの人は特性方程式を学ぶときに混乱します。異なる数字をαに置き換えるため、なぜ特性方程式を利用できるのか理解できないのです。そこで、この理由を知らなければいけません。
また漸化式では、ほかにも特殊な漸化式がたくさんあります。漸化式の解き方は決まっているため、答えを得るためには、問題の解き方を知っているかどうかが重要です。なお問題の解き方を知らない場合、おそらく答えを得ることはできません。ヒントなしで漸化式の問題を解くのは難しいからです。
それでは、どのように特性方程式を利用すればいいのでしょうか。また、特殊な漸化式についてどう答えを得ればいいのでしょうか。漸化式の応用問題の解き方を解説していきます。
もくじ
特性方程式(\(a_{n+1}=pa_n+q\))を利用する漸化式の解き方
漸化式を利用して一般項を得るためには、式を等差数列型、等比数列型、階差数列型のうち、どれかに変形する必要があります。これらの漸化式になっていない場合、式を変形しましょう。このとき利用するのが特性方程式です。
特性方程式を理解するため、例題を解いてみましょう。
- \(a_1=1\)、\(a_{n+1}=3a_n+4\)のとき、一般項を求めましょう。
この漸化式では、等差数列型にも等比数列型にもなっていません。つまり、この状態のままでは一般項を得ることができません。そこで、\(a_{n+1}=α\)、\(a_n=α\)としましょう。これにより、\(α=3α+4\)を作ることができます。この式を特性方程式といいます。
そこで特性方程式を利用して、以下のように引き算をします。
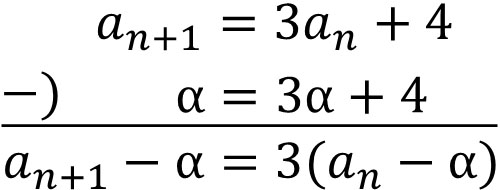
なお\(α=3α+4\)であるため、\(α=-2\)です。そこで、以下のように式を変形しましょう。
\(a_{n+1}-α=3(a_n-α)\)
\(a_{n+1}+2=3(a_n+2)\)
ここで、\(a_n+2=b_n\)としましょう。そうすると、式は以下のように変わります。
\(b_{n+1}=3b_n\)
こうして、\(b_n\)は公比3の等比数列とわかります。そこで、\(b_n\)の初項を計算しましょう。
\(b_1=a_1+2\)
\(b_1=1+2\)
\(b_1=3\)
\(b_n\)の初項は3であるため、一般項は\(b_n=3·3^{n-1}\)\(=3^n\)です。そこで、以下のように計算することで一般項\(a_n\)を得ることができます。
\(b_n=3^n\)
\(a_n+2=3^n\)
\(a_n=3^n-2\)
こうして、特性方程式を利用することで一般項を得ることができました。
なぜ異なる数字をαに置き換えるのか?
なお漸化式の計算で特性方程式を学ぶとき、多くの人が混乱します。\(a_{n+1}\)と\(a_n\)は異なる値です。それにも関わらず、\(a_{n+1}=α\)、\(a_n=α\)と考えて計算します。なぜ、このような計算が成り立つのでしょうか。
漸化式で特性方程式を利用するのは、等比数列へ変形するためです。先ほど記した問題を以下に再び掲載します。
- \(a_{n+1}=3a_n+4\) – ①
この式で邪魔な数字が4です。4がなければ、式は等比数列となります。等比数列型であれば、容易に一般項を得ることができます。そこで等比数列に変形するため、以下のように無理やり形を変えましょう。
- \(a_{n+1}-α=3(a_n-α)\) – ②
αの値が何かは不明です。ただいずれにしても、先ほど解説した通り、この形であれば等比数列型の漸化式を利用することによって一般式を得ることができます。
次に、①から②を引きましょう。そうすると、以下の式を作れます。
- \(α=3α+4\)
こうして、元の式について\(a_{n+1}\)と\(a_n\)をαへ置き換えた場合と同じ式を作ることができました。特性方程式というのは、異なる数字をαにしているわけではありません。式を等比数列にするため、利用される式が特性方程式です。
ただ、ヒントなしで特性方程式を得るのは難しいです。このとき漸化式が\(a_{n+1}=pa_n+q\)の形なのであれば、\(a_{n+1}=α\)、\(a_n=α\)にすることで、特性方程式を作れることがわかっています。そこで、こうした置き換えをするのです。
定数ではなく式に\(n\)を含む場合、階差数列を用いて問題を解く
なお場合によっては、階差数列と特性方程式を用いて一般式を得ることもできます。漸化式の中には、等比数列に加えて「\(n\)を含む式」が加わっていることがあります。つまり、等比数列に定数が加わるのではなく、等比数列と\(n\)を含む式を含んでいるのです。
例えば、以下の問題が該当します。
- \(a_1=1\)、\(a_{n+1}=3a_n+4n\)のとき、一般項を求めましょう。
このように定数ではなく、\(n\)を含む式(今回の例では\(4n\))が存在します。この場合、階差数列を用いて計算します。
\(a_{n+1}=3a_n+4n\)について、\(n\)を\(n+1\)に変えましょう。漸化式は以前の式を利用して答えを得ることができるため、\(n\)を\(n+1\)に変えるのは問題ありません。そうすると、以下の式を得ることができます。
- \(a_{n+2}=3a_{n+1}+4(n+1)\)
そこで\(a_{n+1}=3a_n+4n\)と\(a_{n+2}=3a_{n+1}+4(n+1)\)を利用して、以下のように引き算をしましょう。

このように、階差数列を得ることができます。\(b_n=a_{n+1}-a_n\)とすると、以下の式に変形できます。
- \(b_{n+1}=3b_n+4\)
この式と似た式を先ほど計算したと思います。特性方程式を利用することにより、4(定数)を消去できます。

なお\(α=3α+4\)であるため、\(α=-2\)です。そのため、以下の数列を作れます。
- \(b_{n+1}+2=3(b_n+2)\)
こうして、数列\(\{b_n+2\}\)は公比3の等比数列とわかります。また、初項を計算しましょう。
\(b_1=a_{2}-a_1\)
\(b_1=3+4-1\)
\(b_1=6\)
\(b_1=6\)であるため、数列\(\{b_n+2\}\)の初項は\(6+2=8\)です。つまり、以下のように式を作れます。
\(b_n+2=8·3^{n-1}\)
\(b_n=8·3^{n-1}-2\)
次に、階差数列の一般項\(b_n\)を利用して、元の数列の一般項\(a_n\)を計算しましょう。\(a_1=1\)、\(b_n=8·3^{n-1}-2\)であるため、\(n≧2\)のとき、以下の計算によって一般項\(a_n\)を得ることができます。
\(a_n=1+\displaystyle\sum_{k=1}^{n-1}{(8·3^{k-1}-2)}\)
\(a_n=1+\displaystyle\frac{8(3^{n-1}-1)}{3-1}\)\(-2(n-1)\)
\(a_n=4·3^{n-1}-2n-1\)
なお\(n=1\)のとき、\(a_1=1\)です。\(n=1\)であっても成り立つため、一般項は\(a_n=4·3^{n-1}-2n-1\)です。
特殊な漸化式とパターン
先ほど、2パターンの特殊な漸化式を解説しました。以下の漸化式になります。
- 特性方程式を活用:\(a_{n+1}=pa_n+q\)
- 階差数列を利用:\(a_{n+1}=pa_n+f(n)\)
特殊な漸化式はほかにもパターンがあります。どの漸化式についても、解き方が決まっており、解き方を知っていれば答えを得ることができます。以下が特殊な漸化式になります。
- 指数に\(n\)を含む:\(a_{n+1}=pa_n+q^n\)
- 漸化式が分数を含む:\(a_{n+1}=\displaystyle\frac{a_n}{pa_n+q}\)
- \(a_n\)にルートまたは累乗が含まれる:\(a_{n+1}=pa_n^q\)
- \(a_n\)の係数に\(n\)が含まれる:\(a_{n+1}=f(n)·a_n+q\)
- \(a_n\)の係数に\(n\)が含まれる:\(a_{n+1}=f(n)·a_n\)
漸化式を学ぶとき、すべてのパターンを解けるようになる必要があります。解き方を知っているかどうかが重要になるため、それぞれのパターンを覚えましょう。前述の通り、ヒントなしで漸化式の問題を解くのは難しいからです。
指数に\(n\)を含む漸化式は両辺を指数で割る
\(a_{n+1}=pa_n+q^n\)型の漸化式について、式を\(a_{n+1}=pa_n+q\)型に変えることを考えましょう。これをするため、両辺を\(q^{n+1}\)で割ります。これにより、指数に\(n\)が含まれなくなります。
それでは、以下の問題を解きましょう。
- \(a_1=4\)、\(a_{n+1}=3a_n+2^{n+1}\)によって定められる数列\(\{a_n\}\)の一般項を求めましょう。
式を\(a_{n+1}=pa_n+q\)型に変えるため、両辺を\(2^{n+1}\)で割りましょう。そうすると、式は以下のようになります。
- \(\displaystyle\frac{a_{n+1}}{2^{n+1}}=\displaystyle\frac{3}{2}·\displaystyle\frac{a_n}{2^n}+1\)
そこで、\(b_n=\displaystyle\frac{a_n}{2^n}\)としましょう。これにより、式がわかりやすくなります。
- \(b_{n+1}=\displaystyle\frac{3}{2}b_n+1\)
特性方程式\(α=\displaystyle\frac{3}{2}α+1\)について、式を解くと\(α=-2\)です。また、特性方程式を利用することで式を以下のように変形できます。
- \(b_{n+1}+2=\displaystyle\frac{3}{2}(b_n+2)\)
こうして、数列\(\{b_n+2\}\)は公比\(\displaystyle\frac{3}{2}\)の等比数列とわかりました。また\(b_1=\displaystyle\frac{a_1}{2^1}\)\(=2\)です。\(b_1+2=4\)であるため、初項は4です。そのため、以下の一般項を作れます。
\(b_n+2=4·\left(\displaystyle\frac{3}{2}\right)^{n-1}\)
\(b_n=4·\left(\displaystyle\frac{3}{2}\right)^{n-1}-2\)
\(\displaystyle\frac{a_n}{2^n}=4·\left(\displaystyle\frac{3}{2}\right)^{n-1}-2\)
\(a_n=2^n·4·\left(\displaystyle\frac{3}{2}\right)^{n-1}-2·2^n\)
\(a_n=8·3^{n-1}-2^{n+1}\)
こうして、一般項を得ることができました。
分数を含む漸化式で逆数を利用する
\(a_{n+1}=\displaystyle\frac{a_n}{pa_n+q}\)のように、分子に\(a_n\)のみが含まれている場合、逆数を利用することによって式を\(a_{n+1}=pa_n+q\)型に変えることができます。なお逆数を利用するため、\(a_n≠0\)と示す必要があります。
それでは、以下の問題の答えは何でしょうか。
- \(a_1=1\)、\(a_{n+1}=\displaystyle\frac{a_n}{2a_n+1}\)によって定められる数列\(\{a_n\}\)の一般項を求めましょう。
このように分子と分母に\(a_n\)を含む場合、逆数を利用することで計算できるケースがあります。\(a_1=1\)であり、\(\displaystyle\frac{a_n}{2a_n+1}\)では分母に引き算がありません。そのため\(a_n\)は常に正の値であり、\(a_n≠0\)です。そこで、逆数を利用しましょう。
- \(\displaystyle\frac{1}{a_{n+1}}=\displaystyle\frac{1}{a_n}+2\)
また、\(\displaystyle\frac{1}{a_n}=b_n\)としましょう。
\(b_{n+1}=b_n+2\)
\(b_{n+1}-b_n=2\)
こうして、数列\(\{b_n\}\)は公差2の等差数列とわかります。また初項は\(b_1=\displaystyle\frac{1}{a_1}\)\(=1\)です。そのため、一般項は以下のようになります。
\(b_n=1+(n-1)2\)
\(b_n=2n-1\)
なお\(\displaystyle\frac{1}{a_n}=b_n\)であるため、\(\displaystyle\frac{1}{a_n}=2n-1\)です。そのため、\(a_n=\displaystyle\frac{1}{2n-1}\)が答えとわかります。分数を含む漸化式では、逆数を利用することで答えを得ることができるかどうか確かめましょう。
\(a_n\)にルートまたは累乗が含まれる場合、対数を利用する
\(\sqrt{a_n}\)のように、\(a_n\)がルートを含むケースがあります。または、\(a_n^2\)や\(a_n^3\)のように、\(a_n\)に累乗が存在するケースもあります。この場合、対数を利用しましょう。
対数を加えると、累乗を消去できます。\(\sqrt{a_n}=a_n^{\frac{1}{2}}\)であるため、\(a_n\)がルートを含む場合であっても対数の利用は有効です。対数を利用すれば、\(a_{n+1}=pa_n+q\)型へ変形することができます。
対数を利用するため、\(a_n≠0\)である必要があります。また真数条件も確認しなければいけません。それでは、以下の問題を解いてみましょう。
- \(a_1=1\)、\(a_{n+1}=2\sqrt{a_n}\)によって定められる数列\(\{a_n\}\)の一般項を求めましょう。
\(a_1=1\)であるため、\(a_{n+1}=2\sqrt{a_n}\)は常に正の値です。\(a_n>0\)であり、底を2とする対数を両辺に取りましょう。対数の底については、計算しやすい底を選びましょう。今回の例題では以下の計算になります。
\(log_2a_{n+1}=log_22\sqrt{a_n}\)
\(log_2a_{n+1}=log_22+log_2a_n^{\frac{1}{2}}\)
\(log_2a_{n+1}=\displaystyle\frac{1}{2}log_2a_n+1\)
\(log_2a_n=b_n\)としましょう。そうすると、式は以下のようになります。
- \(b_{n+1}=\displaystyle\frac{1}{2}b_n+1\)
こうして、\(a_{n+1}=pa_n+q\)型へ変形することができました。この式を作ることができれば、特性方程式を利用することによって一般項を計算できます。\(α=\displaystyle\frac{1}{2}α+1\)を利用すると、以下の式を作れます。
- \(b_{n+1}-α=\displaystyle\frac{1}{2}(b_n-α)\)
なお\(α=\displaystyle\frac{1}{2}α+1\)より、\(α=2\)です。そのため、式は以下のようになります。
- \(b_{n+1}-2=\displaystyle\frac{1}{2}(b_n-2)\)
こうして、数列\(\{b_n-2\}\)は公比\(\displaystyle\frac{1}{2}\)の等比数列とわかります。また\(b_1=log_2a_1\)\(=log_21\)\(=0\)です。そのため、初項は\(0-2=-2\)です。つまり、数列\(\{b_n-2\}\)の一般項は以下になります。
\(b_n-2=-2·\left(\displaystyle\frac{1}{2}\right)^{n-1}\)
\(b_n=2-2·\left(\displaystyle\frac{1}{2}\right)^{n-1}\)
\(log_2a_n=b_n\)であるため、以下のように計算しましょう。
\(log_2a_n=2-2·\left(\displaystyle\frac{1}{2}\right)^{n-1}\)
\(log_2a_n=log_22^{2-2·\left(\frac{1}{2}\right)^{n-1}}\)
\(a_n=2^{2-2·\left(\frac{1}{2}\right)^{n-1}}\)
こうして、一般項\(a_n\)を計算することができました。
\(a_n\)の係数に\(n\)が含まれる:\(a_{n+1}=f(n)·a_n+q\)
\(a_n\)の係数に\(n\)が存在する場合、置き換えを利用することで\(a_{n+1}=pa_n+q\)型または\(a_{n+1}=pa_n+f(n)\)型に変形できないか考えましょう。ヒントなしで式を変形するのは難しいですが、式を変形できれば一般項を得ることができます。
それでは、以下の問題の答えは何でしょうか。
- \(a_1=1\)、\(na_{n+1}=2(n+1)a_n\)によって定められる数列\(\{a_n\}\)について、\(b_n=\displaystyle\frac{a_n}{n}\)とするとき、一般項を求めましょう。
前述の通り、ヒントなしで式を変形するのは難しいものの、問題文にヒントとして\(b_n=\displaystyle\frac{a_n}{n}\)が記されているため、このヒントを利用しましょう。
\((n+1)a_n\)について、どのような値で割れば\(\displaystyle\frac{a_n}{n}\)となるでしょうか。\(n(n+1)\)で割れば、\((n+1)a_n\)を\(\displaystyle\frac{a_n}{n}\)へ変えることができます。そこで、式の両辺を\(n(n+1)\)で割りましょう。そうすると、以下の式を得られます。
\(\displaystyle\frac{a_{n+1}}{n+1}=2\displaystyle\frac{a_n}{n}\)
\(b_{n+1}=2b_n\)
こうして、公比2の等比数列を得ることができました。また\(b_1=\displaystyle\frac{a_1}{1}\)\(=1\)です。そのため、\(b_n=2^{n-1}\)となります。なお\(b_n=\displaystyle\frac{a_n}{n}\)であるため、以下のように計算しましょう。
\(b_n=2^{n-1}\)
\(\displaystyle\frac{a_n}{n}=2^{n-1}\)
\(a_n=n·2^{n-1}\)
こうして、置き換えが可能なように\(a_n\)の係数を変形することにより、一般項を計算することができました。
漸化式の繰り返しにより、一般項を得る
\(a_{n+1}=f(n)·a_n\)型の漸化式は先ほど解説した式と同じように、\(a_n\)に係数\(n\)を含みます。ただ、\(a_n\)と\(a_{n+1}\)以外の項がありません。この場合、等差数列や等比数列、特性方程式などを利用せず、漸化式の繰り返しによって一般項を得ることができます。
実際に問題を解かないと意味を理解できないと思うので、以下の練習問題を解いてみましょう。
- \(a_1=1\)、\((n+1)a_n=na_{n-1}\)(\(n≧2\))によって定められる数列\(\{a_n\}\)について、一般項を求めましょう。
まず、両辺を\(n+1\)で割りましょう。この場合、式は以下のようになります。
- \(a_n=\displaystyle\frac{n}{n+1}a_{n-1}\)
それでは、この漸化式を利用して\(a_{n-2}\)を含む式を作るにはどうすればいいでしょうか。先ほどの漸化式を利用すると、\(n\)を\(n-1\)に変換すれば\(a_{n-1}=\displaystyle\frac{n-1}{n}a_{n-2}\)となります。そこで、\(a_{n-1}=\displaystyle\frac{n-1}{n}a_{n-2}\)を代入すると以下の式を得られます。
- \(a_n=\displaystyle\frac{n}{n+1}\)\(·\displaystyle\frac{n-1}{n}a_{n-2}\)
次に、\(a_{n-3}\)を含む式を加えると以下のようになります。
- \(a_n=\displaystyle\frac{n}{n+1}\)\(·\displaystyle\frac{n-1}{n}\)\(·\displaystyle\frac{n-2}{n-1}a_{n-3}\)
そこで、\(a_1\)になるまで漸化式を繰り返しましょう。なお問題文より、\(n≧2\)であるため\(n\)の最小値は2です。
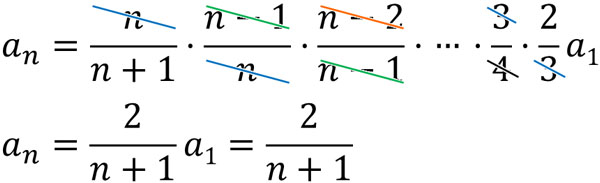
こうして、一般的な漸化式の計算とはまったく異なる方法によって答えを得ることができました。こうした方法によって漸化式を解くケースがあることを学びましょう。
漸化式の解き方には複数の種類がある
漸化式の問題を解くとき、パターンが決まっています。それぞれのパターンについて、階差数列や累乗の割り算、逆数、対数など、さまざまな方法によって式を変形しましょう。
なお、式を\(a_{n+1}=pa_n+q\)型へ変形できれば、特性方程式を利用することによって一般項を得ることができます。漸化式の計算で特性方程式はひんぱんに利用されるため、どのような性質をもつ式なのか理解しましょう。
漸化式の計算で必ず特性方程式を利用するわけではありません。特性方程式なしに漸化式を等差数列型や等比数列型へ変形し、問題を解けることもあります。漸化式の繰り返しにより、一般項を得られるケースもあります。
ヒントなしで漸化式の問題を解くのは難しいです。そこで式を確認することで、問題を解くための方針を立てられるようになりましょう。






